【Pytorch】卷积神经网络实现手写数字识别
【Pytorch】卷积神经网络实现手写数字识别
- 1 加载数据
- 2 模型构建
- 3 训练模型
- 4 模型保存
- 5 模型加载和使用
1 加载数据
分别构建训练集和测试集(验证集)
DataLoader来迭代取数据
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets,transforms
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# 定义超参数
input_size = 28 #图像的总尺寸28*28
num_classes = 10 #标签的种类数
num_epochs = 3 #训练的总循环周期
batch_size = 64 #一个撮(批次)的大小,64张图片
# 训练集
train_dataset = datasets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
# 测试集
test_dataset = datasets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor())
# 构建batch数据
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=True)
2 模型构建
构建卷积神经网络,一般卷积层,relu层,池化层可以写成一个套餐
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Sequential( # 输入大小 (1, 28, 28)
nn.Conv2d(
in_channels=1, # 灰度图
out_channels=16, # 要得到几多少个特征图
kernel_size=5, # 卷积核大小
stride=1, # 步长
padding=2, #
), # 输出的特征图为 (16, 28, 28)
nn.ReLU(), # relu层
nn.MaxPool2d(kernel_size=2), # 进行池化操作(2x2 区域), 输出结果为: (16, 14, 14)
)
self.conv2 = nn.Sequential( # 下一个套餐的输入 (16, 14, 14)
nn.Conv2d(16, 32, 5, 1, 2), # 输出 (32, 14, 14)
nn.ReLU(), # relu层
nn.MaxPool2d(2), # 输出 (32, 7, 7)
)
self.out = nn.Linear(32 * 7 * 7, 10) # 全连接层得到的结果
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0), -1) # flatten操作,结果为:(batch_size, 32 * 7 * 7)
output = self.out(x)
return output
3 训练模型
准确率作为评估标准
def accuracy(predictions, labels):
pred = torch.max(predictions.data, 1)[1]
rights = pred.eq(labels.data.view_as(pred)).sum()
return rights, len(labels)
# 实例化
net = CNN()
#损失函数
criterion = nn.CrossEntropyLoss()
#优化器
optimizer = optim.Adam(net.parameters(), lr=0.001) #定义优化器,普通的随机梯度下降算法
#开始训练循环
for epoch in range(num_epochs):
#当前epoch的结果保存下来
train_rights = []
for batch_idx, (data, target) in enumerate(train_loader): #针对容器中的每一个批进行循环
net.train()
output = net(data)
loss = criterion(output, target)
optimizer.zero_grad() # 梯度归o
loss.backward()
optimizer.step() # 更新优化器的学习率
right = accuracy(output, target)
train_rights.append(right)
if batch_idx % 100 == 0:
net.eval()
val_rights = []
for (data, target) in test_loader:
output = net(data)
right = accuracy(output, target)
val_rights.append(right)
#准确率计算
train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))
val_r = (sum([tup[0] for tup in val_rights]), sum([tup[1] for tup in val_rights]))
print('当前epoch: {} [{}/{} ({:.0f}%)]\t损失: {:.6f}\t训练集准确率: {:.2f}%\t测试集正确率: {:.2f}%'.format(
epoch, batch_idx * batch_size, len(train_loader.dataset),
100. * batch_idx / len(train_loader),
loss.data,
100. * train_r[0].numpy() / train_r[1],
100. * val_r[0].numpy() / val_r[1]))
输出
当前epoch: 0 [0/60000 (0%)] 损失: 2.287790 训练集准确率: 14.06% 测试集正确率: 11.06%
当前epoch: 0 [6400/60000 (11%)] 损失: 0.402259 训练集准确率: 75.60% 测试集正确率: 92.08%
当前epoch: 0 [12800/60000 (21%)] 损失: 0.071038 训练集准确率: 84.53% 测试集正确率: 94.49%
当前epoch: 0 [19200/60000 (32%)] 损失: 0.055919 训练集准确率: 88.09% 测试集正确率: 96.30%
当前epoch: 0 [25600/60000 (43%)] 损失: 0.065247 训练集准确率: 90.17% 测试集正确率: 97.37%
当前epoch: 0 [32000/60000 (53%)] 损失: 0.101428 训练集准确率: 91.52% 测试集正确率: 97.45%
当前epoch: 0 [38400/60000 (64%)] 损失: 0.119459 训练集准确率: 92.52% 测试集正确率: 97.69%
当前epoch: 0 [44800/60000 (75%)] 损失: 0.062872 训练集准确率: 93.21% 测试集正确率: 97.87%
当前epoch: 0 [51200/60000 (85%)] 损失: 0.044197 训练集准确率: 93.75% 测试集正确率: 97.86%
当前epoch: 0 [57600/60000 (96%)] 损失: 0.140018 训练集准确率: 94.13% 测试集正确率: 98.00%
当前epoch: 1 [0/60000 (0%)] 损失: 0.020221 训练集准确率: 100.00% 测试集正确率: 98.44%
当前epoch: 1 [6400/60000 (11%)] 损失: 0.084976 训练集准确率: 98.02% 测试集正确率: 98.33%
当前epoch: 1 [12800/60000 (21%)] 损失: 0.098251 训练集准确率: 97.92% 测试集正确率: 98.39%
当前epoch: 1 [19200/60000 (32%)] 损失: 0.078864 训练集准确率: 98.00% 测试集正确率: 98.47%
当前epoch: 1 [25600/60000 (43%)] 损失: 0.025394 训练集准确率: 98.13% 测试集正确率: 98.40%
当前epoch: 1 [32000/60000 (53%)] 损失: 0.042705 训练集准确率: 98.13% 测试集正确率: 98.28%
当前epoch: 1 [38400/60000 (64%)] 损失: 0.027868 训练集准确率: 98.13% 测试集正确率: 98.57%
当前epoch: 1 [44800/60000 (75%)] 损失: 0.010066 训练集准确率: 98.17% 测试集正确率: 98.57%
当前epoch: 1 [51200/60000 (85%)] 损失: 0.035174 训练集准确率: 98.19% 测试集正确率: 98.68%
当前epoch: 1 [57600/60000 (96%)] 损失: 0.021053 训练集准确率: 98.25% 测试集正确率: 98.61%
当前epoch: 2 [0/60000 (0%)] 损失: 0.004226 训练集准确率: 100.00% 测试集正确率: 98.46%
当前epoch: 2 [6400/60000 (11%)] 损失: 0.012750 训练集准确率: 98.69% 测试集正确率: 98.78%
当前epoch: 2 [12800/60000 (21%)] 损失: 0.071001 训练集准确率: 98.59% 测试集正确率: 98.24%
当前epoch: 2 [19200/60000 (32%)] 损失: 0.116683 训练集准确率: 98.67% 测试集正确率: 98.75%
当前epoch: 2 [25600/60000 (43%)] 损失: 0.082070 训练集准确率: 98.65% 测试集正确率: 98.79%
当前epoch: 2 [32000/60000 (53%)] 损失: 0.011719 训练集准确率: 98.65% 测试集正确率: 98.93%
当前epoch: 2 [38400/60000 (64%)] 损失: 0.044769 训练集准确率: 98.66% 测试集正确率: 98.81%
当前epoch: 2 [44800/60000 (75%)] 损失: 0.181679 训练集准确率: 98.67% 测试集正确率: 99.07%
当前epoch: 2 [51200/60000 (85%)] 损失: 0.022912 训练集准确率: 98.67% 测试集正确率: 98.77%
当前epoch: 2 [57600/60000 (96%)] 损失: 0.084802 训练集准确率: 98.69% 测试集正确率: 98.77%
4 模型保存
# 只保存模型参数
# torch.save(net.state_dict(), 'cov.pkl')
# 加载
# model = CNN()
# model.load_state_dict(torch.load('\cov.pkl'))
# 保存
torch.save(net, 'cov.pkl')
# 加载
#model = torch.load('\cov.pkl')
5 模型加载和使用
model = torch.load('cov.pkl')
print(model)
输出
CNN(
(conv1): Sequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv2): Sequential(
(0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(out): Linear(in_features=1568, out_features=10, bias=True)
)
import cv2
import matplotlib.pyplot as plt
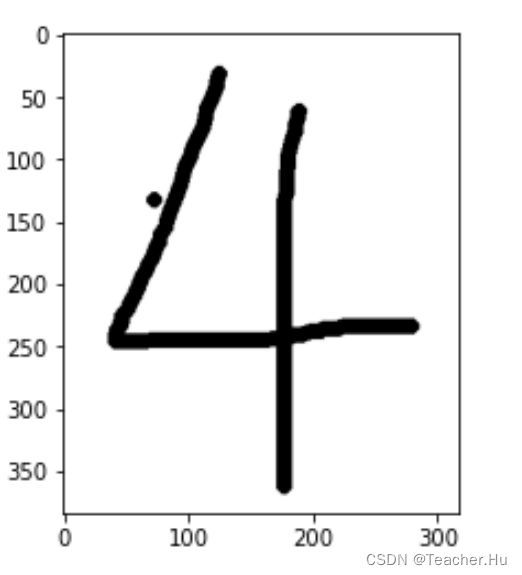
# 第一步:读取图片
img = cv2.imread('./data/test/4.png')
print(img.shape)
# 第二步:将图片转为灰度图
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
print(img.shape)
plt.imshow(img,cmap='Greys')
# 第三步:将图片的底色和字的颜色取反
img = cv2.bitwise_not(img)
plt.imshow(img,cmap='Greys')
# 第四步:将底变成纯白色,将字变成纯黑色
img[img<=144]=0
img[img>140]=255 # 130
# 显示图片
plt.imshow(img,cmap='Greys')
# 第五步:将图片尺寸缩放为输入规定尺寸
img = cv2.resize(img,(28,28))
# 第六步:将数据类型转为float32
img = img.astype('float32')
# 第七步:数据正则化
img /= 255
# 第八步:增加维度为输入的规定格式
img = img.reshape(1,1, 28, 28)
print(img.shape)
# 第九步:预测
pred = model(torch.from_numpy(img))
# 第十步:输出结果
print(pred.argmax())
输出
(384, 317, 3)
(384, 317)
(1, 1, 28, 28)
tensor(4)