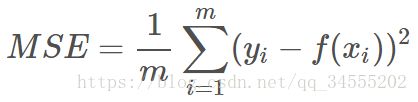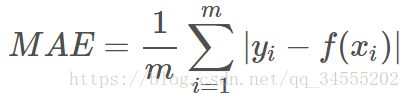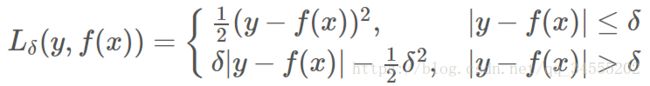无论在机器学习还是深度领域中,损失函数都是一个非常重要的知识点。损失函数（Loss Function）是用来估量模型的预测值 f(x) 与真实值 y 的不一致程度。我们的目标就是最小化损失函数，让 f(x) 与 y 尽量接近。通常可以使用梯度下降算法寻找函数最小值。
损失函数有许多不同的类型，没有哪种损失函数适合所有的问题，需根据具体模型和问题进行选择。一般来说，损失函数大致可以分成两类：回归（Regression）和分类（Classification）。
回归模型中的三种损失函数包括：均方误差（Mean Square Error）、平均绝对误差（Mean Absolute Error，MAE）、Huber Loss。
1. 均方误差（Mean Square Error，MSE）
均方误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离平方的平均值。其公式如下所示：
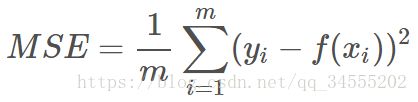
其中，yi 和 f(xi) 分别表示第 i 个样本的真实值和预测值，m 为样本个数。
为了简化讨论，忽略下标 i，m = 1，以 y-f(x) 为横坐标，MSE 为纵坐标，绘制其损失函数的图形：
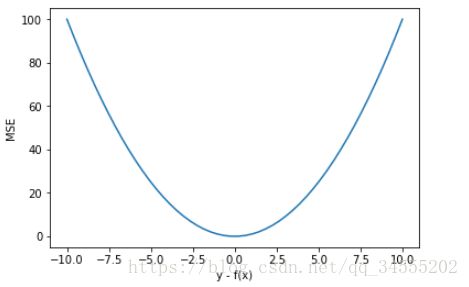
MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。
平方误差有个特性，就是当 yi 与 f(xi) 的差值大于 1 时，会增大其误差；当 yi 与 f(xi) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。
如果样本中存在离群点，MSE 会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。我们来看一下使用 MSE 解决含有离群点的回归模型。
-
import numpy
as np
-
import matplotlib.pyplot
as plt
-
x = np.linspace(
1,
20,
40)
-
y = x + [np.random.choice(
4)
for _
in range(
40)]
-
y[
-5:] -=
8
-
X = np.vstack((np.ones_like(x),x))
# 引入常数项 1
-
m = X.shape[
1]
-
# 参数初始化
-
W = np.zeros((
1,
2))
-
-
# 迭代训练
-
num_iter =
20
-
lr =
0.01
-
J = []
-
for i
in range(num_iter):
-
y_pred = W.dot(X)
-
loss =
1/(
2*m) * np.sum((y-y_pred)**
2)
-
J.append(loss)
-
W = W + lr *
1/m * (y-y_pred).dot(X.T)
-
-
# 作图
-
y1 = W[
0,
0] + W[
0,
1]*
1
-
y2 = W[
0,
0] + W[
0,
1]*
20
-
plt.scatter(x, y)
-
plt.plot([
1,
20],[y1,y2])
-
plt.show()
拟合结果如下图所示：
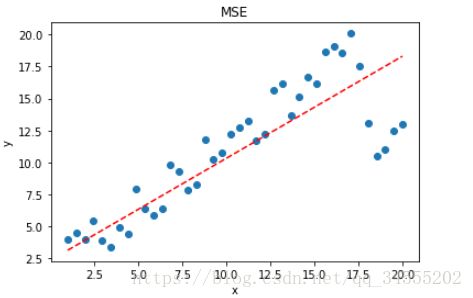
可见，使用 MSE 损失函数，受离群点的影响较大，虽然样本中只有 5 个离群点，但是拟合的直线还是比较偏向于离群点。这往往是我们不希望看到的。
2. 平均绝对误差（Mean Absolute Error，MAE）
平均绝对误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离的平均值。其公式如下所示：
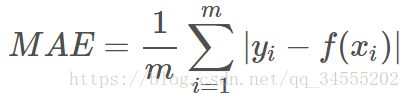
为了简化讨论，忽略下标 i，m = 1，以 y-f(x) 为横坐标，MAE 为纵坐标，绘制其损失函数的图形：
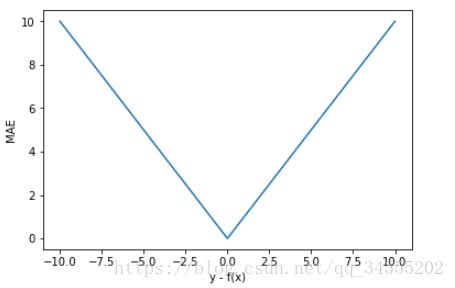
直观上来看，MAE 的曲线呈 V 字型，连续但在 y-f(x)=0 处不可导，计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。
值得一提的是，MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感，更有包容性。因为 MAE 计算的是误差 y-f(x) 的绝对值，无论是 y-f(x)>1 还是 y-f(x)<1，没有平方项的作用，惩罚力度都是一样的，所占权重一样。针对 MSE 中的例子，我们来使用 MAE 进行求解，看下拟合直线有什么不同。
-
X = np.vstack((np.ones_like(x),x))
# 引入常数项 1
-
m = X.shape[
1]
-
# 参数初始化
-
W = np.zeros((
1,
2))
-
-
# 迭代训练
-
num_iter =
20
-
lr =
0.01
-
J = []
-
for i in range(num_iter):
-
y_pred = W.dot(X)
-
loss =
1/m * np.sum(np.abs(y-y_pred))
-
J.append(loss)
-
mask = (y-y_pred).copy()
-
mask[y-y_pred >
0] =
1
-
mask[mask <=
0] =
-1
-
W = W + lr *
1/m * mask.dot(X.T)
-
-
# 作图
-
y1 = W[
0,
0] + W[
0,
1]*
1
-
y2 = W[
0,
0] + W[
0,
1]*
20
-
plt.scatter(x, y)
-
plt.plot([
1,
20],[y1,y2],
'r--')
-
plt.xlabel(
'x')
-
plt.ylabel(
'y')
-
plt.title(
'MAE')
-
plt.show()
注意上述代码中对 MAE 计算梯度的部分。
拟合结果如下图所示：
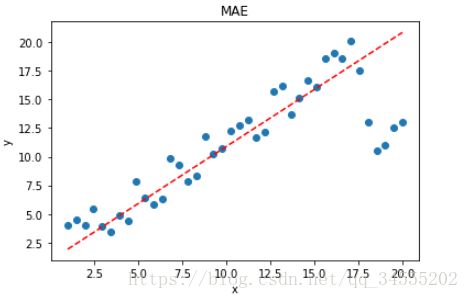
显然，使用 MAE 损失函数，受离群点的影响较小，拟合直线能够较好地表征正常数据的分布情况。这一点，MAE 要优于 MSE。二者的对比图如下：
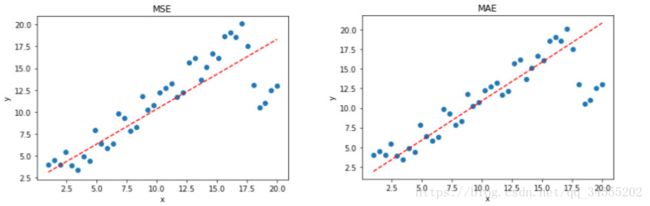
选择 MSE 还是 MAE 呢？
实际应用中，我们应该选择 MSE 还是 MAE 呢？从计算机求解梯度的复杂度来说，MSE 要优于 MAE，而且梯度也是动态变化的，能较快准确达到收敛。但是从离群点角度来看，如果离群点是实际数据或重要数据，而且是应该被检测到的异常值，那么我们应该使用MSE。另一方面，离群点仅仅代表数据损坏或者错误采样，无须给予过多关注，那么我们应该选择MAE作为损失。
3. Huber Loss
既然 MSE 和 MAE 各有优点和缺点，那么有没有一种激活函数能同时消除二者的缺点，集合二者的优点呢？答案是有的。Huber Loss 就具备这样的优点，其公式如下：
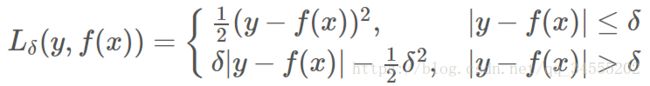
Huber Loss 是对二者的综合，包含了一个超参数 δ。δ 值的大小决定了 Huber Loss 对 MSE 和 MAE 的侧重性，当 |y−f(x)| ≤ δ 时，变为 MSE；当 |y−f(x)| > δ 时，则变成类似于 MAE，因此 Huber Loss 同时具备了 MSE 和 MAE 的优点，减小了对离群点的敏感度问题，实现了处处可导的功能。
通常来说，超参数 δ 可以通过交叉验证选取最佳值。下面，分别取 δ = 0.1、δ = 10，绘制相应的 Huber Loss，如下图所示：
Huber Loss 在 |y−f(x)| > δ 时，梯度一直近似为 δ，能够保证模型以一个较快的速度更新参数。当 |y−f(x)| ≤ δ 时，梯度逐渐减小，能够保证模型更精确地得到全局最优值。因此，Huber Loss 同时具备了前两种损失函数的优点。
下面，我们用 Huber Loss 来解决同样的例子。
-
X = np.vstack((np.ones_like(x),x))
# 引入常数项 1
-
m = X.shape[
1]
-
# 参数初始化
-
W = np.zeros((
1,
2))
-
-
# 迭代训练
-
num_iter =
20
-
lr =
0.01
-
delta =
2
-
J = []
-
for i in range(num_iter):
-
y_pred = W.dot(X)
-
loss =
1/m * np.sum(np.abs(y-y_pred))
-
J.append(loss)
-
mask = (y-y_pred).copy()
-
mask[y-y_pred > delta] = delta
-
mask[mask < -delta] = -delta
-
W = W + lr *
1/m * mask.dot(X.T)
-
-
# 作图
-
y1 = W[
0,
0] + W[
0,
1]*
1
-
y2 = W[
0,
0] + W[
0,
1]*
20
-
plt.scatter(x, y)
-
plt.plot([
1,
20],[y1,y2],
'r--')
-
plt.xlabel(
'x')
-
plt.ylabel(
'y')
-
plt.title(
'MAE')
-
plt.show()
注意上述代码中对 Huber Loss 计算梯度的部分。
拟合结果如下图所示：
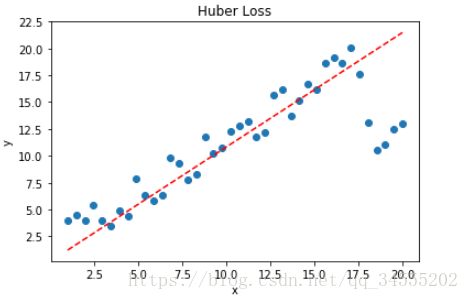
可见，使用 Huber Loss 作为激活函数，对离群点仍然有很好的抗干扰性，这一点比 MSE 强。另外，我们把这三种损失函数对应的 Loss 随着迭代次数变化的趋势绘制出来：
MSE：
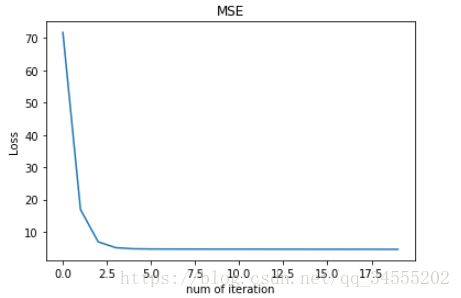
MAE：
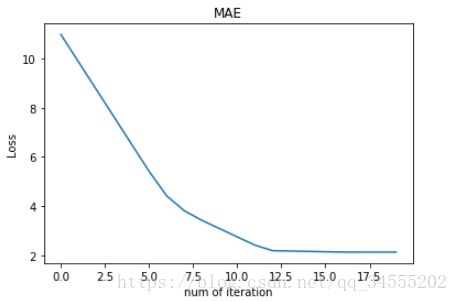
Huber Loss：
对比发现，MSE 的 Loss 下降得最快，MAE 的 Loss 下降得最慢，Huber Loss 下降速度介于 MSE 和 MAE 之间。也就是说，Huber Loss 弥补了此例中 MAE 的 Loss 下降速度慢的问题，使得优化速度接近 MSE。
最后，我们把以上介绍的回归问题中的三种损失函数全部绘制在一张图上。
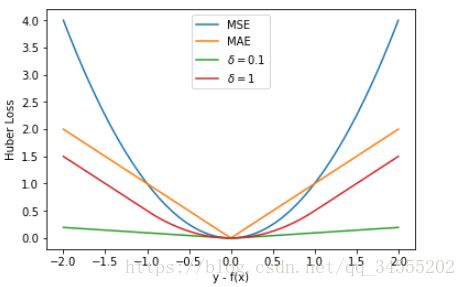
好了，以上就是红色石头对回归问题 3 种常用的损失函数包括：MSE、MAE、Huber Loss 的简单介绍和详细对比。这些简单的知识点你是否已经完全掌握了呢？
05-02 阅读数 1万+
一、线性回归损失函数的两种解释线性回归的损失函数是平方损失函数，为什么使用平方的形式，参考：线性回归损失函数为什么要用平方形式，讲得很清楚。在线性回归中，对于训练数据样本(xi,yi)(x_i,y_i... 博文 来自： wjlucc的专栏
07-03 阅读数 873
案例来源：@AI科技评论案例地址：https://mp.weixin.qq.com/s/Gt8Q4Wm36DoNBO4xI8SJAw1.MSE（均方误差，L2）1）损失函数是预测与目标之间的误差平方和... 博文 来自： 数据产品笔记
04-15 阅读数 10万+
有监督学习机器学习分为有监督学习，无监督学习，半监督学习，强化学习。对于逻辑回归来说，就是一种典型的有监督学习。既然是有监督学习，训练集自然可以用如下方式表述：{(x1,y1),(x2,y2),⋯,(... 博文 来自： bitcarmanlee的博客
06-18 阅读数 2954
翻译|张建军编辑|阿司匹林出品|AI科技大本营【AI科技大本营导读】机器学习中的所有算法都依赖于最小化或最大化某一个函数，我们称之为“目标函数”。最小化的这组...... 博文 来自： AI科技大本营
05-21 阅读数 128
机器学习中的所有算法都依赖于最小化或最大化函数，我们将其称为“目标函数”。最小化的函数组称为“损失函数”。损失函数是衡量预测模型在能够预测预期结果方面的表现有多好的指标。寻找最小值的最常用方法是“梯度... 博文 来自： 陨星落云的博客
08-28 阅读数 794
大数据文摘出品编译：Apricock、睡不着的iris、JonyKai、钱天培“损失函数”是机器学习优化中至关重要的一部分。L1、L2损失函数相信大多数人都早已不陌生。那你了解Huber损失、Log-... 博文 来自： chduan_10的博客
03-21 阅读数 1205
首先说什么是凸函数。对区间[a,b]上定义的函数f，若它对区间中任意两点x1和x2，均有f((x1+x2)/2)<=(f(x1)+f(x2))/2，则称f为区间[a,b]上的凸函数。对实... 博文 来自： 一路向北
05-09 阅读数 4746
欢迎使用Markdown编辑器写博客1.交叉熵CrossEntropy交叉熵与熵相对，如同协方差与方差熵考察的是单个的信息（分布）的期望：H(p)=−∑i=1np(xi)logp(xi)H(p)=-\... 博文 来自： zeng
开源人脸识别软件有哪些?
大观
损失函数的选择
05-22 阅读数 1487
神经网络需要选择的有：1网络结构模型 2激活函数 3损失函数学习训练设计到：1优化，训练集训练参数 2泛化，测试集优化参数---------------------------------------... 博文 来自： rickhuan的博客
回归损失函数: L1 Loss
05-07 阅读数 437
平均绝对误差，L1损失平均绝对误差（MAE）是另一种用于回归模型的损失函数。MAE是目标变量和预测变量之间绝对差值之和。因此它衡量的是一组预测值中的平均误差大小，而不考虑它们的方向（如果我们考虑方向的... 博文 来自： 小花生的博客
机器学习最常用的5个“”回归损失函数”
04-25 阅读数 275
本文系总结自文章机器学习大牛最常用的5个回归损失函数，你知道几个？。详细讲解请直接前往，本文只作为作者的笔记列出。误差=真实值-预测值。1MAE（L1损失）与MSE（L2损失）1.1MAE与MSE的定... 博文 来自： 张之海的博客
Logistic损失函数证明
09-25 阅读数 7044
在理解Logistic回归算法原理中我们指出了Logistic回归的损失函数定义（在这里重新约定符号）：对于单个样本而言，令为样本的期望输出，记为y；为样本的实际输出，记为y_hat，那么Logist... 博文 来自： chaibubble
逻辑回归损失函数与最大似然估计
09-07 阅读数 858
机器学习的损失函数是人为设计的，用于评判模型好坏（对未知的预测能力）的一个标准、尺子，就像去评判任何一件事物一样，从不同角度看往往存在不同的评判标准，不同的标准往往各有优劣，并不冲突。唯一需要注意的就... 博文 来自： xiaocong1990的博客
![]()
回归损失函数：Log-Cosh Loss
05-07 阅读数 559
Log-Cosh损失函数Log-Cosh是应用于回归任务中的另一种损失函数，它比L2损失更平滑。Log-cosh是预测误差的双曲余弦的对数。优点：对于较小的X值，log(cosh(x))约等于(x**... 博文 来自： 小花生的博客
常见回归和分类的损失函数
03-21 阅读数 170
分类和回归是机器学习中研究的两大目标。分类即预测未知数据的类别，分类模型的输出可以是离散的，也可以是连续的，一般是输出每个类别的概率，分类分为二元分类和多元分类，二元分类如逻辑回归（LR）、支持向量机... 博文 来自： mdh25259mdh的博客
线形回归与损失函数
01-24 阅读数 909
假设特征和结果都满足线性。即不大于一次方。这个是针对收集的数据而言。收集的数据中，每一个分量，就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数，向量表示形式：这个就... 博文 来自： GOODDEEP
LR回归原理和损失函数的推导
07-05 阅读数 1116
博文 来自： zrh_CSDN的博客
DNN深度神经网络损失函数选择
05-25 阅读数 21
文章目录损失函数的类别：专业名词中英文对照损失函数的类别：1.均方误差（MSE）、SVM的合页损失（hingeloss）、交叉熵（crossentropy）2.相对熵相对熵又称KL散度，用于衡量对于同... 博文 来自： 小禅：缠者，人性之纠结，贪嗔疾慢疑也；禅者，觉悟、超脱者也。
![]()
机器学习里必备的五种回归损失函数
11-29 阅读数 142
所有的机器学习算法都或多或少的依赖于对目标函数最大化或者最小化的过程。我们常常将最小化的函数称为损失函数，它主要用于衡量模型的预测能力。在寻找最小值的过程中，我们最常用的方法是梯度下降法，这种方法很像... 博文 来自： mbshqqb的博客
Mac安装Brew
11-11 阅读数 276
安装命令如下：curl-LsSfhttp://github.com/mxcl/homebrew/tarball/master|sudotarxvz-C/usr/local--strip1当brew安装... 博文 来自： weixin_34104341的博客
回归问题的损失函数
04-14 阅读数 1147
PRML里有一节讲了回归问题的损失函数，用到了泛函和变分法，但是推导过于简略，这里补充一下详细过程。首先平均损失为：如果损失函数用均方误差，则为：设则根据变分法有当取极值时，满足条件然后做如下推导：由... 博文 来自： github_15579971的博客
常见问题类型的最后一层激活和损失函数选择
01-14 阅读数 567
问题类型 最后一层激活 损失函数 二分类问题 sigmoid binary_crossentropy 多分类、单标签问题 softmax categorical_cross... 博文 来自： qq_35419086的博客
损失函数
12-27 阅读数 23
1.交叉熵、相对熵、信息熵、条件熵https://blog.csdn.net/huwenxing0801/article/details/82791879... 博文 来自： qq_28978767的博客
我们为什么这样选择损失函数
07-22 阅读数 2007
我们为什么这样选择损失函数这个问题深度学习中的“圣经”花书中进行阐述，这里做一个简单的总结和自己的思考。先从信息熵开始说起信息论的基本想法是一个不太可能发现的事件居然发生了，要比一个非常可能的事件发生... 博文 来自： 记录学习的过程
干货 | 深度学习之损失函数与激活函数的选择
09-19 阅读数 3414
微信公众号关键字全网搜索最新排名【机器学习算法】：排名第一【机器学习】：排名第二【Python】：排名第三【算法】：排名第四前言在深度神经网络（DNN）反向传播算法(BP)中，我们对DNN的前向反向传... 博文 来自： 机器学习算法与Python学习
激活函数与对应的损失函数选择(binary与multi-class如何选择损失函数)
03-24 阅读数 297
之前一段时间，对激活函数和损失函数一直是懵懂的状态，只知道最后一层常用的激活函数是sigmoid或者softmax，而损失函数一般用的是cross-entropy或者diceloss(我看的都是分割方... 博文 来自： normol的博客
深层神经网络——分类、回归的损失函数
07-18 阅读数 1万+
神经网络模型的效果以及优化目标是通过损失函数（lossfunction）来定义的。分类问题和回归问题有很多经典的损失函数。分类问题和回归问题是监督学习的两大种类。分类问题希望解决的是将不同的样本分到事... 博文 来自： 魂小猫的博客
【机器学习精研】——5种常见的回归损失函数
10-14 阅读数 348
【引言】所有机器学习算法都旨在最小化或最大化目标函数，其中，将目标函数最小化的过程称为损失函数。损失函数：是衡量预测模型预测期望结果表现的指标。常用方法为梯度下降法，通过设置一定的步长，让函数在求导的... 博文 来自： 锟金铐鏜鏜鏜
LogisticRegression(逻辑回归，对率回归）损失函数推导
03-05 阅读数 266
昨天面试遇到的问题，今天整理出来。主要是损失函数的推倒。预测函数y=H(x)=11+e−(ωTx+b)y=H(x)=\frac{1}{1+e^{-(\boldsymbol{\mathbf{}\omeg... 博文 来自： wangcaimeng的博客
回归测试用例选择方法
07-14
先说什么是回归测试，顾名思义，回归测试就是修改完bug之后对程序的新的一轮测试。据微软的统计，按照他们的经验，一般开发人员解决3~4个bug 会衍生出一个新的bug，这就是必须作回归测试的原因。。。。
具体内容请查看《回归测试用例选择方…
下载
回归或分类算法选择
08-09 阅读数 8
Oftenthehardestpartofsolvingamachinelearningproblemcanbefindingtherightestimatorforthejob.Differente... 博文
模型评估、选择与验证——损失函数
04-14 阅读数 1029
0-1损失函数模型原型sklearn.metrics.zero_one_loss(y_true,y_pred,normalize=True,sample_weight=None)参数y_true:样本... 博文 来自： As的博客
机器学习大牛最常用的5个回归损失函数，你知道几个？
06-24 阅读数 576
“损失函数”是机器学习优化中至关重要的一部分。L1、L2损失函数相信大多数人都早已不陌生。那你了解Huber损失、Log-Cosh损失、以及常用于计算预测区间的分位数损失么？这些可都是机器学习大牛... 博文 来自： Nine days
Keras自带Loss Function研究
04-21 阅读数 228
本文研究Keras自带的几个常用的LossFunctions。categorical_crossentropyVS.sparse_categorical_crossentropy先看categoric... 博文 来自： Forskamse's Blog
【深度学习】：回归 & 分类任务的Loss函数分析
07-03 阅读数 2378
L1&amp;amp;amp;amp;L2loss代码importtensorflowastfimportmatplotlib.pyplotaspltsess=tf.Session()... 博文 来自： yuanCruise
训练分类器为什么要用cross entropy loss（交叉熵损失函数）而不能用mean square error loss（MSE,最小平方差损失函数）?
05-10 阅读数 5887
在一个人工智能群里，有人问起，训练分类器为什么要用crossentropyloss（交叉熵损失函数）而不能用meansquareerrorloss（MSE,最小平方差损失函数）呢?正好，在我的那本《深... 博文 来自： 玉来愈宏的随笔
Huber Loss function
02-22 阅读数 74
转自：https://blog.csdn.net/lanchunhui/article/details/50427055 博文 来自： 岁月流星0824的博客
知网查重的几个原理你知道吗?
大观
神经网络输出层激活函数与损失函数选择
02-14 阅读数 1294
问题 激活函数 损失函数 回归 identity MES/ SQUARED_LOSS 分类 二分类 单标签输出 sigmoid XENT 二... 博文 来自： bewithme的专栏
分类问题中，常选择交叉熵损失函数而不是MSE损失函数
06-17 阅读数 70
均方误差(MeanSquareError,MSE)损失函数：对求偏导（对求导类似）：交叉熵损失函数：对求偏导（对求导类似）：ps：以上公式中，激活函数取sigmod激活函数参数更新过程：对比公式(2)... 博文 来自： tianyunzqs的专栏
回归只是最开始的选择
03-26 阅读数 347
已经近两年没有回csdn写博客了。从一个技术控，慢慢的去学习了解市场，了解产品。这两年更多的在市场里，想找到更好的创业产品。毕竟有梦想的人，就要去做有梦想的事。 希望自己还是能找到做任何事情的初心。不... 博文 来自： 梦想启航者
损失函数——交叉熵损失函数【转】
03-29 阅读数 38
这篇文章对交叉熵损失讲的比较透彻，同时也浅显易懂，请参考。https://zhuanlan.zhihu.com/p/35709485... 博文 来自： weixin_41813620的博客
交叉熵损失函数和均方误差损失函数
04-19 阅读数 3612
交叉熵 分类问题中，预测结果是（或可以转化成）输入样本属于n个不同分类的对应概率。比如对于一个4分类问题，期望输出应该为g0=[0,1,0,0]，实际输出为g1=[0.2,0.4,0.4,0]，计算g... 博文 来自： 牧野的博客
平方损失函数与交叉熵损失函数
05-07 阅读数 9180
1.前言在机器学习中学习模型的参数是通过不断损失函数的值来实现的。对于机器学习中常见的损失函数有：平方损失函数与交叉熵损失函数。在本文中将讲述两者含义与响应的运用区别。2.平方损失函数平方损失函数较为... 博文 来自： m_buddy的博客
如何学损失函数
06-01 阅读数 211
今天无意间看到了logistic回归的pytorch的实现，抱着他山之石可以攻玉的态度，阅读了一下代码，突然发现在其代码中的网络搭建部分只有一个Linear层，却不见softmax层（使用的是mnis... 博文 来自： qq_20945297的博客
L1损失函数和L2损失函数
05-11 阅读数 187
L1损失函数：最小化绝对误差，因此L1损失对异常点有较好的适应更鲁棒，不可导，有多解，解的稳定性不好。关于L1损失函数的不连续的问题，可以通过平滑L1损失函数代替：L2损失函数：最小化平方误差，因此L... 博文 来自： Andy_Zhao的博客
没有更多推荐了，返回首页
你可能感兴趣的:(如何选择回归损失函数)
