《数字图像处理第二版》第一、二章部分习题
习题
- 第一章 绪论
-
- 习题1
-
-
- 什么是数字图像?
-
- 习题2
-
-
- 什么是像素?
-
- 第二章 数字图像基础
-
- 习题1
-
-
-
- 7mmx7mm的CCD芯片有1024x1024元素,将其聚焦到相距0.5m远的方形平坦区域。该摄像机每毫米能解析多少线对?摄像机配置35mm镜头。
-
-
- 习题2
-
-
-
- 数字数据传输速率通常用为每秒钟传输的比特数度量。通常的传输是以一个开始比特、一个字节(8比特)的信息和一个停止比特组成的包完成的。基于这个概念回答下列问题:
- (a)用56K波特的调制调解器传输一幅1024x1024、256级灰度的图像要多长时间?
- (b)以750K的调制调解器传输要用多少时间?
-
-
- 习题3
-
-
-
- 已知一点p的坐标是(x,y),请写出 N 4 ( p ) N_4(p) N4(p), N D ( p ) N_D(p) ND(p), N 8 ( p ) N_8(p) N8(p)
-
-
- 习题4
-
-
-
- 两个图像子集S1和S2如下图所示,对于V={1},确定这两个子集是4邻接,8邻接,还是m邻接。
-
-
- 习题5
-
-
-
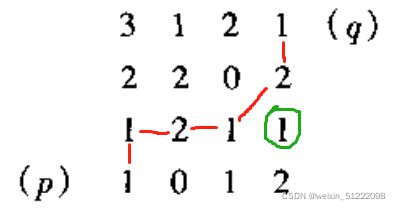
- 考虑如下所示的图像:
- (a)令V={0,1},并计算p和q间的4,8,m通路的最短长度。
- (b)对V={1,2}重复上题。
-
-
- 习题6
-
-
-
- 已知一副数字图像 f ( x , y ) f(x,y) f(x,y),其中 f ( 0 , 0 ) = 100 f(0,0)=100 f(0,0)=100, f ( 0 , 1 ) = 150 f(0,1)=150 f(0,1)=150, f ( 1 , 0 ) = 200 f(1,0)=200 f(1,0)=200, f ( 0 , 0 ) = 100 f(0,0)=100 f(0,0)=100, f ( 1 , 1 ) = 250 f(1,1)=250 f(1,1)=250。
- (1)用邻近插值求 f ( 0.4 , 0.4 ) f(0.4,0.4) f(0.4,0.4);
- (2)用双线性插值求 f ( 0.4 , 0.4 ) f(0.4,0.4) f(0.4,0.4)
-
-
- 习题7
-
-
-
- 已知图像尺寸为61.44x61.44 c m 2 cm^2 cm2,每个像素为0.12x0.12 c m 2 cm^2 cm2,且量化为16灰度级,求:
- 1)该图像需要多大的存储容量(Byte)
- 2)可能构成多少种不同的数字图像
-
-
- 习题8
-
-
-
- 有同学认为m邻接消除了8邻接的二义性,所以任何两点间只有一条m通路, D m D_m Dm距离就是m通路的长度。
-
-
- 习题9
-
-
-
- 什么是线性操作?什么是非线性操作?
-
-
第一章 绪论
习题1
什么是数字图像?
答:一幅图像可定义为一个二维函数f(x,y),这里x和y是空间坐标,而在任何一对空间坐标(x,y)上的幅值f称为该点图像的强度或灰度。当x,y和幅值f为有限的、离散的数值时,称该图像为数字图像。
习题2
什么是像素?
答:数字图像是由有限的元素组成的,每一个元素都有一个特定的位置和幅值,这些元素称为图像元素、画面元素或像素。
第二章 数字图像基础
视觉感知要素;图像的获取、取样和量化;像素间的一些基本关系
习题1
7mmx7mm的CCD芯片有1024x1024元素,将其聚焦到相距0.5m远的方形平坦区域。该摄像机每毫米能解析多少线对?摄像机配置35mm镜头。
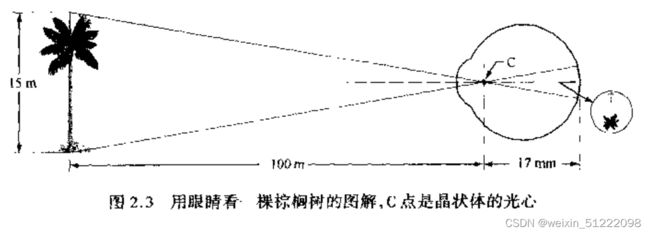
分析:空间分辨率是图像中可辨别的最小细节,单位距离的可分辨线对数反映了在原始场景中分析细节的能力。一个线对是由两条线组成,要能分辨它至少应有两个像素,如果能求得原始场景中单位距离的成像数目就能求出可分辨线对数。那么应该利用教材中图2.3的成像模型来求解。
解:先求原始场景中1mm在CCD芯片上的成像大小如下图:
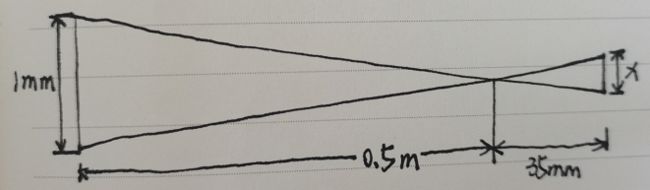
由 x 35 = 1 500 \frac{x}{35}=\frac{1}{500} 35x=5001,可得x=0.07mm,在0.07mm的CCD芯片上的元素数为 1024 7 × 0.07 = 10.24 \frac{1024}{7}\times0.07=10.24 71024×0.07=10.24,每毫米能解析的线对数为 10.24 2 = 5.12 \frac{10.24}{2}=5.12 210.24=5.12
习题2
数字数据传输速率通常用为每秒钟传输的比特数度量。通常的传输是以一个开始比特、一个字节(8比特)的信息和一个停止比特组成的包完成的。基于这个概念回答下列问题:
(a)用56K波特的调制调解器传输一幅1024x1024、256级灰度的图像要多长时间?
(b)以750K的调制调解器传输要用多少时间?
分析:首先应计算图像数据的大小,再计算实际传输的比特数大小,最后根据调制调节器的速率算出所需的时间。
解:
(a)图像为256级灰度,每像素需要8比特,图像数据的大小为:102410248=8388608比特
实际传输的比特数为:8388608/810=10485760 比特
花费时间: 10485760/(561000)=187.2 秒
(b)花费时间: 10485760/(750*1000)=13.98 秒
习题3
已知一点p的坐标是(x,y),请写出 N 4 ( p ) N_4(p) N4(p), N D ( p ) N_D(p) ND(p), N 8 ( p ) N_8(p) N8(p)
答:
p的4领域像素集(有4个水平和垂直的相邻像素)
N 4 ( p ) N_4(p) N4(p):{(x+1,y),(x-1,y),(x,y+1),(x,y-1)}
p的对角领域像素集(有4个对角邻像素)
N D ( p ) N_D(p) ND(p): {(x+1,y+1),(x+1,y-1),(x-1,y-1),(x-1,y+1)}
p的8领域像素集(有4个水平和垂直的相邻像素和4个对角邻像素)
N 8 ( p ) N_8(p) N8(p):{(x+1,y),(x-1,y),(x,y+1),(x,y-1),(x+1,y+1),(x+1,y-1),(x-1,y-1),(x-1,y+1)}
习题4
两个图像子集S1和S2如下图所示,对于V={1},确定这两个子集是4邻接,8邻接,还是m邻接。
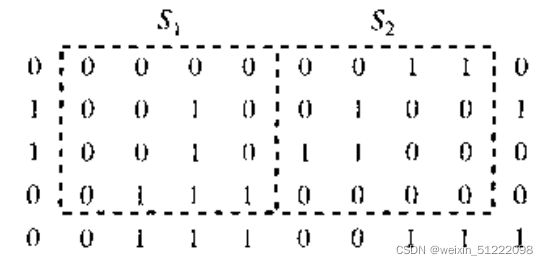
分析:根据3种类型的邻接性定义:
(a)4邻接:如果q在 N 4 ( p ) N_4(p) N4(p)集中,具有V中数值的两个像素p和q是4邻接的。
(b)8邻接:如果q在 N 8 ( p ) N_8(p) N8(p)集中,则具有V中数值的两个像素p和q是8邻接的。
(c)m邻接(混合邻接):如果(i)q在 N 4 ( p ) N_4(p) N4(p)中,或者(ii)q在 N D ( p ) N_D(p) ND(p)中且集合 N 4 ( p ) N_4(p) N4(p)∩ N 4 ( q ) N_4(q) N4(q)没有V值的像素,则具有V值像素p和q是m邻接的。
如果S1中的某像素与S2中的某些像素邻接,则两个图像子集S1和S2是相邻接的。
解:S1和S2不是4邻接,是8邻接也是m邻接。
step1:判断是否的4邻接,发现不是

step2:判断是否是8邻接,结论二者是8邻接。

step3:判断是否是m邻接,结论二者是m邻接。

习题5
考虑如下所示的图像:
(a)令V={0,1},并计算p和q间的4,8,m通路的最短长度。
(b)对V={1,2}重复上题。

分析:从具有坐标( x , y x,y x,y)的像素p到具有坐标( s , t s,t s,t)的像素q的通路(或曲线)是特定像素序列,其坐标为:( x 0 , y 0 x_0,y_0 x0,y0),( x 1 , y 1 x_1,y_1 x1,y1),…,( x n , y n x_n,y_n xn,yn),这里( x 0 , y 0 x_0,y_0 x0,y0)=( x , y x,y x,y),( x n , y n x_n,y_n xn,yn)=( s , t s,t s,t),并且像素( x i , y i x_i,y_i xi,yi)和( x i − 1 , y i − 1 x_i-1,y_i-1 xi−1,yi−1)(对于 1 ⩽ i ⩽ n 1\leqslant i \leqslant n 1⩽i⩽n)是邻接的。在这种情况下,n是通路的长度。
(a)p到q之间没有4通路,最短8通路长度为4,最短m通路长度为5
step1:4通路行不通
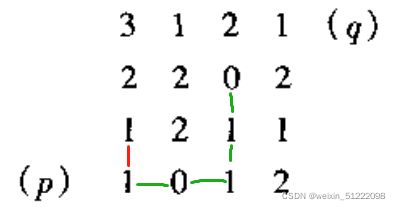
step2:8通路有两条,最短通路长度为4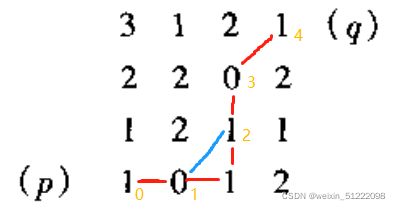
step3:最短m通路长度为5

(b)p到q之间没有4通路,最短8通路长度为4,最短m通路长度为5
step1:最短4通路长度为6
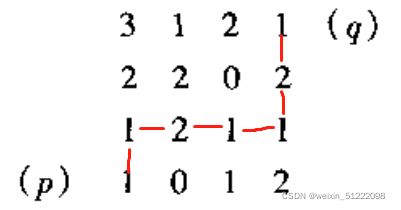
step2:最短8通路长度为4

step2:最短m通路长度为6
习题6
已知一副数字图像 f ( x , y ) f(x,y) f(x,y),其中 f ( 0 , 0 ) = 100 f(0,0)=100 f(0,0)=100, f ( 0 , 1 ) = 150 f(0,1)=150 f(0,1)=150, f ( 1 , 0 ) = 200 f(1,0)=200 f(1,0)=200, f ( 0 , 0 ) = 100 f(0,0)=100 f(0,0)=100, f ( 1 , 1 ) = 250 f(1,1)=250 f(1,1)=250。
(1)用邻近插值求 f ( 0.4 , 0.4 ) f(0.4,0.4) f(0.4,0.4);
(2)用双线性插值求 f ( 0.4 , 0.4 ) f(0.4,0.4) f(0.4,0.4)
分析:邻近插值的结果其实就是最近的整数坐标像素的灰度级。而双线性插值则要根据邻近的四个整数像素值计算。双线性插值可以看成分别在两个方向上作一维线性插值。一维线性插值的原理如下图:
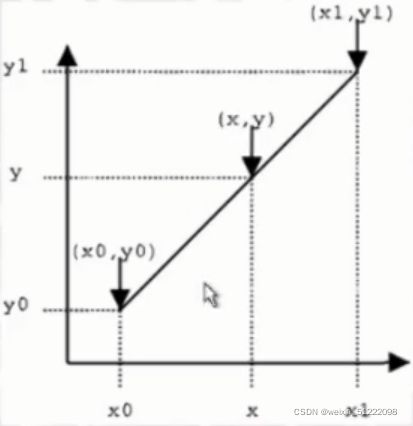
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的值,y=y0-(y0-y1)[(x-x0)/(x1-x0)]
解:
(1)根据邻近插值
f(0.4,0.4)=f(0,0)=100
(2)
先利用一维线性插值计算f(0.4,0)和f(0.4,1)
f(0.4,0)=0.6xf(0,0)+0.4xf(1,0)=140
f(0.4,1)=0.6xf(0,1)+0.4xf(1,1)=190
再利用一维线性插值计算f(0.4,0.4)
f(0.4,0.4)=0.6xf(0.4,0)+0.4xf(0.4,0)=160
习题7
已知图像尺寸为61.44x61.44 c m 2 cm^2 cm2,每个像素为0.12x0.12 c m 2 cm^2 cm2,且量化为16灰度级,求:
1)该图像需要多大的存储容量(Byte)
2)可能构成多少种不同的数字图像
解:
1)该图像需要的存储容量为
61.44 × 61.44 0.12 × 0.12 × 4 ÷ 8 = 131072 \frac{61.44 \times 61.44}{0.12 \times 0.12}\times4\div8=131072 0.12×0.1261.44×61.44×4÷8=131072(Byte)
2) 该图像的像素数目为512*512,每个像素的取值有16种,可能构成的数字图像的种数为 1 6 512 × 512 16^{512\times512} 16512×512
习题8
有同学认为m邻接消除了8邻接的二义性,所以任何两点间只有一条m通路, D m D_m Dm距离就是m通路的长度。
答:错误, D m D_m Dm距离应为最短m通路的长度。
例如下图

对于v={1},在pq之间有两条m通路,其中一条长度为4,一条长度为6,它们的m距离应为最短的m通路长度4.
习题9
什么是线性操作?什么是非线性操作?
答:令H是一种算子,其输入和输出都是图像。如果对于任何两幅图像f和g及任何两个标量a和b有如下关系,则称H为线性算子:H(af+bg)=aH(f)+bH(g)
换句话说,对两幅图像(用所示的常数去乘)的和应用线性算子等同于分别对图像应用概算自,并各自与适当的常数相乘,然后将结果相加。不能通过上式检验的算子就定义为非线性算子。