NeRF_pytorch学习

代码：https://github.com/pylittlebrat/NeRF_recurrence

run_nerf_helpers.py

class Embedder

Positional encoding(section 5.1)
作用：定义位置编码
$\gamma (p)=(sin(2^0\pi p),cos(2^0\pi p),\cdots ,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))$

class NeRF

get_rays

get_rays() 函数与 get_rays_np() 函数基本是一致的，只不过是 torch.meshgrid(a, b) 返回的是 a.shape() 行 ，b.shape() 列的二维数组。因此需要一个转置操作 i.t() ，其余步骤相同。
至此我们生成了每个方向下的像素点到光心的单位方向（Z 轴为 1）。我们有了这个单位方向就可以通过调整 Z 轴坐标生成空间中每一个点坐标，借此模拟一条光线。

get_rays_np

作用：输出相机origin和世界坐标系下的direction

sample_pdf

作用：生成密度函数，用于fine-net网络光线采点

run_nerf

def batchify(fn, chunk):

作用：构造一个适用于较小批次的’fn’版本，将编码后的数据按chunk的规则加入网络

def run_network(inputs, viewdirs, fn, embed_fn, embeddirs_fn, netchunk=1024*64):

作用：将对 input 进行处理，应用 粗网络中；
viewdirs： 视图方向

embedded = embed_fn(inputs_flat)  # 对输入进行位置编码，得到编码后的结果，是一个 array 数组
		...
if viewdirs is not None:
		# 条件为真输入了视图方向，将视角d进行编码
		...
outputs_flat = batchify(fn, netchunk)(embedded)  # 将编码过的点以批处理的形式输入到 网络模型 中得到 输出（RGB,A）

def batchify_rays(rays_flat, chunk=1024*32, **kwargs):

for i in range(0, rays_flat.shape[0], chunk):#一轮循环一个 chunk
ret = render_rays(rays_flat[i:i+chunk], **kwargs)# 往 render_rays() 传入一个 chunk 的 rays

def render(H, W, K, chunk=1024*32, rays=None, c2w=None, ndc=True,near=0., far=1., use_viewdirs=False, c2w_staticcam=None,**kwargs):

Input:

• H：图像的高度（以像素为单位）。
• W：诠释。图像的宽度（以像素为单位）。
• focal：浮动。针孔相机的焦距。
• chunk：整数。即并行处理的光线的数量，曾经控制最大内存使用量。不影响最终结果。
• rays：形状数组 [2, batch_size, 3]。射线原点和方向批处理中的每个示例。
• c2w：形状数组 [3, 4]。相机到世界的变换矩阵。
• ndc：布尔值。如果为 True，则表示 NDC 坐标中的射线原点、方向。
• near：浮点数或形状数组 [batch_size]。射线的最近距离。
• far：浮点数或形状数组 [batch_size]。射线的最远距离。
• use_viewdirs：布尔值。如果为 True，则使用模型中空间点的观察方向。
• c2w_staticcam：形状数组 [3, 4]。如果不是 None，请使用此转换矩阵相机，同时使用其他 c2w 参数查看方向。

Returns:

• rgb_map：[batch_size，3]。光线的预测 RGB 值。
• disp_map：[batch_size]。视差图。深度的倒数。
• acc_map：[batch_size]。沿射线的累积不透明度 (alpha)。
• extras：包含 render_rays() 返回的所有内容的字典。

TODO:
Step 1:调用get_rays()函数，根据光线的 ray_d 计算单位方向作为 view_dirs
Step 2:生成光线的远近端，用于确定边界框，并将其聚合到 rays 中（获得光线的 ray_o、ray_d、near、far、viewdirs）
Step 3:并行计算ray的属性（通过调用batchify_rays()函数）
Step 4:batchify_rays()再调用render_rays()函数进行后续渲染
Step 5:render_rays()的pts属性保存每个采样点的位置
Step 6:将点投入网络，得到RGB与$\sigma$
Step 7:render_rays()调用raw2outputs()函数进行离散点的积分操作(体素渲染)
Step 8:将{‘rgb_map’ : rgb_map, ‘disp_map’ : disp_map, ‘acc_map’ : acc_map}属性传入train中

def render_path(render_poses, hwf, K, chunk, render_kwargs, gt_imgs=None, savedir=None, render_factor=0):

def create_nerf(args):

def raw2outputs(raw, z_vals, rays_d, raw_noise_std=0, white_bkgd=False, pytest=False):

Input:

• raw: [num_rays, num_samples along ray, 4]. Prediction from model.
• z_vals: [num_rays, num_samples along ray]. Integration time.
• rays_d: [num_rays, 3]. Direction of each ray.

Returns:

• rgb_map: [num_rays, 3]. Estimated RGB color of a ray.
• disp_map: [num_rays]. Disparity map. Inverse of depth map.
• acc_map: [num_rays]. Sum of weights along each ray.
• weights: [num_rays, num_samples]. Weights assigned to each sampled color.
• depth_map: [num_rays]. Estimated distance to object.

沿着光线的所有采样颜色的加权和:

raw2alpha = lambda raw, dists, act_fn=F.relu: 1.-torch.exp(-act_fn(raw)*dists)
alpha = raw2alpha(raw[...,3] + noise, dists)  # [N_rays, N_samples]
weights = alpha * torch.cumprod(torch.cat([torch.ones((alpha.shape[0], 1)), 1.-alpha + 1e-10], -1), -1)[:, :-1]
rgb_map = torch.sum(weights[...,None] * rgb, -2)  # [N_rays, 3]

def render_rays(ray_batch,network_fn,network_query_fn, N_samples,retraw=False,lindisp=False,perturb=0.,N_importance=0,network_fine=None,white_bkgd=False,raw_noise_std=0.,verbose=False,pytest=False):

参数：
ray_batch：形状数组 [batch_size, …]。沿射线采样所需的所有信息，包括：射线原点、射线方向、最小距离、最大距离和单位幅度观察方向。
network_fn：功能。用于预测空间中每个点的 RGB 和密度的模型。
network_query_fn：用于将查询传递给 network_fn 的函数。
N_samples：整数。沿每条射线采样的不同次数。
retraw：布尔值。如果为 True，则包括模型的原始、未处理的预测。
lindisp：布尔值。如果为 True，则以反深度而不是深度线性采样。
perturb：浮点数，0 或 1。如果非零，则每条射线都以分层采样
随机时间点。
N_importance：整数。沿每条射线采样的额外次数。
这些样本仅传递给 network_fine。
network_fine：与 network_fn 具有相同规格的“精细”网络。
white_bkgd：布尔值。如果为真，则假定为白色背景。
raw_noise_std: …
ver bose：布尔值。如果为 True，则打印更多调试信息。
回报：
rgb_map：[num_rays，3]。光线的估计 RGB 颜色。来自精品模型。
disp_map：[num_rays]。视差图。 1 / 深度。
acc_map：[num_rays]。沿每条光线累积的不透明度。来自精品模型。
raw：[num_rays，num_samples，4]。来自模型的原始预测。
rgb0：见 rgb_map。粗略模型的输出。
disp0：见 disp_map。粗略模型的输出。
acc0：见 acc_map。粗略模型的输出。
z_std：[num_rays]。每个样本沿射线的距离标准偏差。

	...
	# 确定空间中一个坐标的 Z 轴位置
	t_vals = torch.linspace(0., 1., steps=N_samples)  # 在 0-1 内生成 N_samples 个等差点
	# 根据参数确定不同的采样方式,从而确定 Z 轴在边界框内的的具体位置
	if not lindisp:
        z_vals = near * (1.-t_vals) + far * (t_vals)
    else:
        z_vals = 1./(1./near * (1.-t_vals) + 1./far * (t_vals))

    z_vals = z_vals.expand([N_rays, N_samples])
    ...
    # 生成光线上每个采样点的位置
	pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None]  # [N_rays, N_samples, 3]
	# 将光线上的每个点投入到 MLP 网络 network_fn 中前向传播得到每个点对应的 （RGB，A）
	raw = network_query_fn(pts, viewdirs, network_fn)
	# 对这些离散点进行体积渲染，即进行积分操作
	rgb_map, disp_map, acc_map, weights, depth_map = raw2outputs(raw, z_vals, rays_d, raw_noise_std, white_bkgd, pytest=pytest)
	

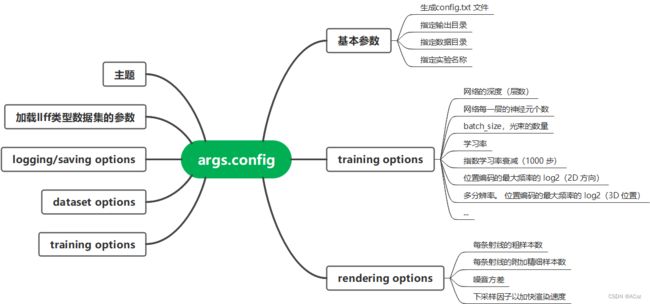
def config_parser():

train

Debug 笔记

以fern数据集为例

Load data

images :{ndarray:(20,378,504,3)（N,H,W,ch）}
poses:{ndarray:(20,3,4)}{[图片数量] ,[相机姿势],[高, 宽, focal,length] }
bds:{ndarray:(20,2)} 用于定义场景范围
render_poses:{ndarray:(120,3,5)}
i_test:12
hwf:{ndarray:(3,)}

Create nerf model

optimizer = Adam
grad_vars:{list:48}
render_kwargs_train（render_kwargs_test ）: {
‘network_query_fn’ : network_query_fn,
‘perturb’ : args.perturb,
‘N_importance’ : args.N_importance,
‘network_fine’ : model_fine,
‘N_samples’ : args.N_samples,
‘network_fn’ : model,
‘use_viewdirs’ : args.use_viewdirs,
‘white_bkgd’ : args.white_bkgd,
‘raw_noise_std’ : args.raw_noise_std,
}

render_kwargs_test = {k : render_kwargs_train[k] for k in render_kwargs_train}
render_kwargs_test['perturb'] = False
render_kwargs_test['raw_noise_std'] = 0.

Prepare raybatch tensor if batching random rays

get_rays_np函数：生成图片每个pixel对应的ray，并转化为世界坐标系下的origin和diretion

rays = [get_rays_np(H, W, focal, p) for p in poses[:, :3, :4]]

rays :{ndarray:(20,2,378,504,3)} {N,[原点，方向向量],W,H,3}
rays_rgb:{ndarray:(3238704,3,3)(N* H* W,[原点,方向向量,RGB},3)}

rays marching

    i, j = np.meshgrid(np.arange(W, dtype=np.float32), np.arange(H, dtype=np.float32), indexing='xy')

i:{ndarray:(378,504)}
j:{ndarray:(378,504)}

dirs = np.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -np.ones_like(i)], -1)

K = np.array([
[focal, 0, 0.5W],
[0, focal, 0.5H],
[0, 0, 1]
# 利用相机内参 K 计算每个像素坐标相对于光心的单位方向

dirs:{ndarray:(378,504,3)} {计算得到相机坐标系下，穿过像素中心的ray}

    # Rotate ray directions from camera frame to the world frame
    rays_d = np.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1)  # dot product, equals to: [c2w.dot(dir) for dir in dirs]

如图，空间中一点 P 经过光心 O （小孔）在成像平面上呈一点 P’ ，并且呈一个倒立的像。我们以光心所在的面建立相机坐标系，那么光心所在的位置可以表示为$(\frac{W}{2},\frac{H}{2},0)$，成像点 P’ 的位置可以表示为 $(i,j,-f)$。由此两点位置，我们可以确定一个方向向量$O{P}^{\prime }=(i-\frac{W}{2},j-\frac{H}{2},-f)$ 。由于小孔成像呈一个倒立的像，因此我们对 $O{P}^{\prime }$ 的 Y 轴坐标取反，并对 $O{P}^{\prime }$的 Z 轴归一化。我们得到一个新的方向向量：$((i-\frac{W}{2})/f,-(j-\frac{H}{2})/f,-1)$。
由此公式我们得到每个像素点关于光心 O 的方向 dirs 。随后我们利用相机外参转置矩阵将相机坐标转换为世界坐标。
rays_d:{ndarray:(378,504,3)} {世界坐标系下的方向向量}

dirs[…, np.newaxis, :] 增加一维,将最后两维度广播到3*3，与c2w相乘。

    # Translate camera frame's origin to the world frame. It is the origin of all rays.
    rays_o = np.broadcast_to(c2w[:3,-1], np.shape(rays_d))

rays_o:{ndarray:(378,504,3)}

Train

use_batching:True
batch:{tensor:(3,1024,3)}
batch_rays:{tensor:(2,1024,3)}
i_train:{ndarray:(17,)}
i_test:{ndarray:(3,)}

rgb:{tensor:(1024,3)}
disp:{tensor:(1024,)}
acc:{tensor:(1024,)}
extras:{dict: 5 }{‘raw’: , ‘rgb0’: , ‘disp0’: , ‘acc0’:, ‘z_std’: )}