《深度学习入门》第5章实战:手写数字识别——误差反向传播
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、一点介绍
-
- (一)计算图
- (二)反向传播
- (三)反向传播的代码表示
- 二、利用误差反向传播进行手写数字识别
-
- 全部代码
- 运行结果
前言
最近阅读了《深度学习入门——基于Python的理论与实现》这本书的第五章,这一章主要讲解的是误差反向传播法——一个相比于数值微分而言,能够高效计算权重参数的梯度的方法。
一、一点介绍
误差反向传播法,是用来计算神经网络的权重参数的梯度的。该方法旨在从后往前遍历一遍神经网络,从而能够计算出损失函数对网络中所有模型参数的梯度。
(一)计算图
书上用计算图来解释误差反向传播法。使用计算图的最大原因是,可以通过反向传播高效计算导数。比如说,下面的图片中就解释了“苹果价格的上涨会在多大程度上影响最终支付金额”这个问题,即求“支付金额关于苹果的价格的导数”这个问题。
那么为什么要通过反向传播计算导数呢?如果能计算出导数,就能知道神经网络权重参数的梯度,从而就能够根据梯度对参数进行更新,从而找到最优参数。
(二)反向传播
在简单介绍了计算图之后,作者还讲解了反向传播的方法,重点介绍了加法节点的反向传播、乘法节点的反向传播。
(三)反向传播的代码表示
上面我们介绍了加法节点和乘法节点的反向传播方式,下面我们将以代码的形式来实现他们的反向传播。
下面,把要实现计算图的乘法节点称作“乘法层”,加法节点称作“加法层”。
- 乘法层的代码实现
class MulLayer:
def __init__(self):
self.x = None
self.y = None
# 这是正向传播
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
# 这里就是反向传播
def backward(self, dout):
dx = dout * self.y # 根据(二)中所讲的,乘法节点的反向传播需要把x和y进行翻转
dy = dout * self.x
return dx, dy
- 加法层的代码实现
class AddLayer:
def __init__(self):
pass # 加法层无需进行初始化,所以直接pass即可
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
看完概念后,结合代码再理解一次,突然有点悟了。书中还讲解了激活函数relu、sigmoid函数等的反向传播推导,在这里就不一一介绍了。
二、利用误差反向传播进行手写数字识别
在这个例子中,神经网络采用的是2层神经网络,该网络使用一个TwoLayerNet类来实现。TwoLayerNet类中的变量说明如下:
params:保存神经网络参数的字典型变量。params[‘W1’]是第1层的权重,params[‘b1’]是第1层的偏置,params[‘W2’]是第2层的权重,params[‘b2’]是第2层的偏置.
layers:保存神经网络的层的有序字典型变量,依次保存了Affine1层、ReLu1层、Affine2层。
lastLayer:神经网络的最后一层。本例中为SoftmaxWithLoss层。
下面说一下几个主要函数:
下面这个函数是TwoLayerNet类的初始化函数。从代码中可以看出,该神经网络采用的是2层神经网络。从前到后依次是Affine层、ReLu层、Affine层、SoftmaxWithLoss层。
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
下面这个函数def gradient(self, x, t)主要用来计算权重参数的梯度。x是图像数据,t是图像的标签。self.loss(x, t)是正向传播的过程,用来计算预测的损失。然后就是backward反向传播的过程。在反向传播的过程中,使用layers.reverse()先把这些层的顺序都倒置,然后再逐层反向传播,最终得到dout,把更新后的参数值放到grad{}里面。
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
下面这个函数def predict(self, x)是用来进行预测的。神经网络的正向传播只需要按照添加元素的顺序调用各层的forward方法就可以完成处理。
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
下面我们来康一康“主函数”的逻辑。说明都写在注释里了。
# 加载数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 超参数
iters_num = 10000 # 随机抽数据,抽10000次
train_size = x_train.shape[0] # 训练集的大小
batch_size = 100 # 随机抽数据,每次抽100个数据
learning_rate = 0.1 # 学习率
train_loss_list = []# 记录训练集的损失值
train_acc_list = [] # 记录训练集的准确度
test_acc_list = [] # 记录测试集的准确度
# 平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 获取mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 记录学习过程
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 计算每个epoch的识别精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
全部代码
PS:下述代码是我根据书上代码敲的,跑代码之前别忘了在官网上下载相应的包common和dataset,放到项目路径venv\Lib\site-packages中去。
官网链接:http://www.ituring.com.cn/book/1921
然后,先点击右侧的“随书下载”,再点击第二个“下载”即可。
放好了就像这样:

来看代码:
import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from common.functions import *
from common.gradient import numerical_gradient
from common.layers import *
from collections import OrderedDict
from dataset.mnist import load_mnist
from dataset.two_layer_net import TwoLayerNet
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def sigmoid(a):
return 1 / (1 + np.exp(-a))
def softmax(a):
exp_a = np.exp(a)
sum = np.sum(exp_a)
y = exp_a / sum
return y
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x是输入数据,t是标签
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 超参数
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 获取mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 记录学习过程
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 计算每个epoch的识别精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
# 导入数据
m = list(np.arange(1, iters_num + 1))
n = list(np.arange(1, len(train_acc_list) + 1))
t = list(np.arange(1, len(test_acc_list) + 1))
# 绘图命令
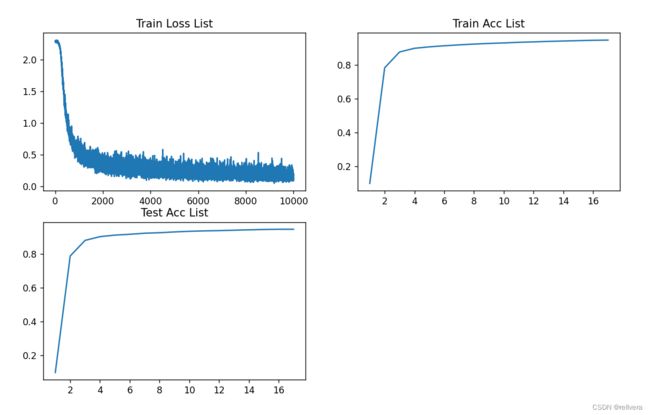
print(train_loss_list)
print(train_acc_list)
print(test_acc_list)
# 画第一个图
plt.subplot(221)
plt.title("Train Loss List")
plt.plot(m, train_loss_list)
# 画第二个图
plt.subplot(222)
plt.title("Train Acc List")
plt.plot(n, train_acc_list)
# 画第三个图
plt.subplot(223)
plt.title("Test Acc List")
plt.plot(t, test_acc_list)
# show出图形
plt.show()