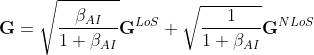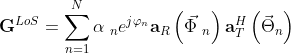智能反射面RIS经典论文复现，主被动式波束赋形
引言
本文主要复现IRS经典论文《Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming》中的单用户部分，给出相应的matlab代码，通过该论文可以了解IRS优化中的一个经典的优化方法，即半正定松弛（SDR）算法，并了解响应的对比算法，如IRS相位随机优化，无IRS以及AP-user最大比发送（MRT），AP-IRS MRT等等。对于多用户部分后续进行补充。具体解释部分可参考博文基于SDR的智能反射面波束成形设计。
该论文引用到1000多次，但是没有在网上找到相应的源码，因此复现以帮助自己理解，代码除高斯随机化部分参考相关网页，其他都是自己书写，该文主要关注复现，其他算法细节请仔细阅读该论文，文章不再详细描述，发出来希望对大家对做IRS相关的工作有用处。
本文主要内容
该论文主要是联合基站主动式和IRS被动式波束赋形优化，以最小化基站的发射功率，并以用户的QoS为约束，考虑了单用户和多用户的场景，本文首先复现单用户的场景，复现结果和论文的结果除数值有些差距，趋势基本吻合，可能某些参数没有对齐，也没有找到相应的参数，但是不影响对于算法的理解。其仿真场景如下
仿真场景
场景中AP和IRS在同一水平线上，用户离AP-IRS水平线的距离为
，AP到用户的水平距离为 
，AP和IRS的距离为 
,其他具体参数可以参考论文的实验部分，在此不在赘述。其优化问题如下
优化问题
为求解该问题，文中将其构造成一个齐次的二次约束二次规划问题（QCQP），然后转化为一个SDR问题，如下
求解优化问题
有秩1约束，求解过程中先舍去该约束，该问题是一个标准的SDP问题，可以利用CVX求解，然后利用高斯随机化过程恢复
，求得次优解，其恢复过程在该论文的GLOBECOM会议的版本中有详细描述，简述如下，首先对SDP得到的 V 进行特征值分解 
，然后令
，其中
，随机产生多个
,然后选取使得目标函数最大的
，最后恢复![\boldsymbol{v}=e^{j \arg \left(\left[\frac{\bar{v}}{\bar{v}_{N+1}}\right]_{(1: N)}\right)}](http://img.e-com-net.com/image/info8/c38dbda2fc034626b3043c1db94dbb97.gif){kind=small}
，详细解释可参考经典的SDR算法（下）：SDR的具体使用细节与相关代码。
信道模型
在通信优化问题的仿真中，信道建模尤其关键，如果信道选择不好会极大地影响优化的性能，可能调试很久都没有出现较为理想的曲线都是因为信道模型选取的问题，主要是小尺度衰落模型的选取。该论文中路径损耗模型如下
其中 
为单位距离的路径损耗，设置为-30 dB， 
为单位距离1m， 
为路径损耗因子，为两个设备之间的距离。
对于小尺度衰落部分，论文中考虑的是莱斯信道模型，AP-IRS之间的信道如下所示：
是莱斯因子，控制LOS分量和NLOS分量的大小关系，
和 
分别是确定性的LoS分量和NLoS分量，其中NLoS分量满足瑞利衰落，对于LoS分量，由于论文中将基站和IRS分别建模为均匀线性阵列（ULA）和均匀面阵（UPA），由于论文中没有详述该部分的内容，在此进行简单的描述，一般ULA配置在x轴上，IRS在xz平面，需要利用UPA的导向矢量（水平和竖直方向导向矢量进行克罗内克积）乘以ULA的导向矢量，即
其中
为路径数，
和
为第n条路径的幅度和相位，
和
分别为发送和接收导向矢量，
和
分别为AoD和AoA的方位角和俯仰角。
对于水平沿着x轴的ULA，
为入射波与y轴的方向，其导向矢量为
![\mathbf{a}(\theta)=\left[1, e^{j 2 \pi \frac{d}{\lambda} \sin (\theta)}, \cdots, e^{j 2 \pi(M-1) \frac{d}{\lambda} \sin (\theta)}\right]^T](http://img.e-com-net.com/image/info8/830adf38e0a8492db0ce5af7b0fe598e.gif){kind=small}
在3D信道模型中，UPA布置在xoz平面上，
，其中为方位角，
为俯仰角， ⊗ 为克罗内克积，导向矢量如下所示
![\mathbf{a}_{\mathrm{az}}(\theta, \phi) =\left[1, e^{j 2 \pi \frac{d}{\lambda} \sin (\theta) \cos (\phi)}, \cdots, e^{j 2 \pi\left(M_H-1\right) \frac{d}{\lambda} \sin (\theta) \cos (\phi)}\right]^T](http://img.e-com-net.com/image/info8/e832afba4333438cbd33ba0fc6061028.gif){kind=small}
![\mathbf{a}_{\mathrm{el}}(\phi) =\left[1, e^{j 2 \pi \frac{d}{\lambda} \sin (\phi)}, \cdots, e^{j 2 \pi\left(M_V-1\right) \frac{d}{\lambda} \sin (\phi)}\right]^T](http://img.e-com-net.com/image/info8/29431ad2ccfe45d6bf765cebea758cdd.gif){kind=small}
其中为阵元之间的距离，通常设置为半波长，
为波长。
为简化仿真，该论文中AP和IRS正对着，即实际上AoA和AoD都为0°，论文实验中设置，
即AP和IRS之间只有一条LoS路径，没有NLoS部分，信道可简化为全一矩阵乘以路损，即使加上一个相位因素对优化结果没有影响，因此可以舍去信道延迟造成的相位偏转。而IRS和user以及AP和user之间是服从纯瑞利衰落信道。对于信道模型的选取，特别是否含有LoS路径也是通信优化中需要着重考虑的因素，会极大地影响优化的性能和调试过程。
仿真代码
仿真参数设置
clc
clear
epsilon = 1e-4; % 收敛停止条件
d0 = 51; % AP到IRS之间的距离
dv = 2; % 两条竖线之间的距离
% d = 50; % User和AP之间的水平距离
% d1 = sqrt(d^2+dv^2); % AP到User之间的距离
% d2 = sqrt((d0-d)^2+dv^2); % User到IRS之间的距离
C0 = db2pow(-30); % 参考距离时的路损
D0 = 1; % 参考距离
sigmaK2 = db2pow(-80); % 噪声功率
gamma = db2pow(10); % 信干噪比约束10dB
L = @(d, alpha)C0*(d/D0)^(-alpha); % 路损模型
% 路损参数
alpha_AI = 2;
alpha_Iu = 2.8;
alpha_Au = 3.5;
beta_IU = 0; % IRS到User考虑瑞利衰落信道，AP和IRS之间为纯LoS信道
% 天线数
M = 4; % AP天线数
N = 30; % IRS单元个数 仿真主循环
需要说明的是在此对信道根据噪声功率进行了归一化操作，使得信道参数数量级不至于太小，如果信道参数的数量级很小，CVX也难以进行优化，最好使得信道参数的数据集在1e-2次方以上，归一化并不影响目标函数的大小，是通信优化中的小技巧，有时候根据信道模型产生的信道参数难以得到较好的优化结果时，可以考虑进行归一化操作。
需要注意的是，根据第三节B部分求解得到的v，求共轭转置的时候，只需要进行转置，不然相位没有进行对齐，这里容易出现错误。
d = 20:5:50; % User和AP之间的水平距离
frame = 500;
P1 = zeros(length(d),1);
P2 = zeros(length(d),1);
P3 = zeros(length(d),1);
P4 = zeros(length(d),1);
P5 = zeros(length(d),1);
P6 = zeros(length(d),1);
P7 = zeros(length(d),1);
for i = 1:length(d)
i
d1 = sqrt(d(i)^2+dv^2); % AP到User之间的距离
d2 = sqrt((d0-d(i))^2+dv^2); % User到IRS之间的距离
for j = 1:frame
G = sqrt(L(d0,alpha_AI))*ones(N,M); % LoS信道,除以噪声功率是为了进行噪声功率归一化，因为G和hr是级联的，对一个信道进行归一化即可
hr = sqrt(L(d2,alpha_Iu)/(2*sigmaK2))*(randn(1,N)+1i*randn(1,N)); % 瑞利信道, IRS-User
hd = sqrt(L(d1,alpha_Au)/(2*sigmaK2))*(randn(1,M)+1i*randn(1,M)); % 瑞利信道, IRS-User
% SDR优化方法，得到下界
[v, lower_bound] = SDR_solving(hr, G, hd, N);
P_opt = gamma/(norm(v'*(diag(hr)*G)+hd)^2);
P1(i) = P1(i) + P_opt;
P4(i) = P4(i) + gamma / lower_bound;
% AP-User MRT
[v_aumrt, w_aumrt] = AUMRT(hd,hr,G);
P_aumrt = gamma/(norm((v_aumrt.'*(diag(hr)*G)+hd)*w_aumrt)^2); % 注意这里的相位对齐后，对v只需要转置即可，不需要共轭转置
P2(i) = P2(i) + P_aumrt;
% AP-IRS MRT
[v_aimrt, w_aimrt] = AIMRT(hd,hr,G);
P_aimrt = gamma/(norm((v_aimrt.'*(diag(hr)*G)+hd)*w_aimrt)^2);
P3(i) = P3(i) + P_aimrt;
% 交替迭代算法
P_AO = AO(hd,hr,G,epsilon,gamma);
P7(i) = P7(i) + P_AO;
% IRS随机相位算法
theta = 2*pi*rand(1,N); % 随机初始化IRS的相位
Theta = diag(exp(1i*theta));
P_rand = gamma / (norm(hr*Theta*G+hd)^2);
P5(i) = P5(i) + P_rand;
% 无IRS的场景
P6(i) = P6(i) + gamma / (norm(hd)^2);
end
end
P1 = pow2db(P1 / frame);
P2 = pow2db(P2 / frame);
P3 = pow2db(P3 / frame);
P4 = pow2db(P4 / frame);
P5 = pow2db(P5 / frame);
P6 = pow2db(P6 / frame);
P7 = pow2db(P7 / frame);
plot(d, P1, 'g-','LineWidth',2.5)
hold on
plot(d, P2, 'r^-.','LineWidth',2)
plot(d, P3, 'cv-.','LineWidth',2)
plot(d, P4, 'mo-','LineWidth',1)
plot(d, P5, 'kp:','LineWidth',2)
plot(d, P6, 'ks:','LineWidth',2)
plot(d, P7, 'b:','LineWidth',2)
xlabel('AP-user horizontal distance, d(m)')
ylabel('Transmit power at the AP (dBm)')
grid on
legend('SDR','AP-suer MRT','AP-IRS MRT','Lower bound','Random pahse shift','Without IRS','Alternating optimization','location','best')SDR优化
function [v, lower_bound] = SDR_solving(hr, G, hd, N)
L = 1000; % 高斯随机化过程次数
Phi = diag(hr)*G;
R = [Phi*Phi' Phi*hd'; hd*Phi' 0];
cvx_begin sdp quiet
variable V(N+1,N+1) hermitian
maximize(real(trace(R*V))+norm(hd)^2);
subject to
diag(V) == 1;
V == hermitian_semidefinite(N+1);
cvx_end
lower_bound = cvx_optval;
% 高斯随机化过程
%% method 1
max_F = 0;
max_v = 0;
[U, Sigma] = eig(V);
for l = 1 : L
r = sqrt(2) / 2 * (randn(N+1, 1) + 1j * randn(N+1, 1));
v = U * Sigma^(0.5) * r;
if v' * R * v > max_F
max_v = v;
max_F = v' * R * v;
end
end
v = exp(1j * angle(max_v / max_v(end)));
v = v(1 : N);
endAP-user MRT以及AP-IRS MRT
该部分算法是给定基站波束的发射方向，按直接链路进行最大比发送，或者按照与IRS信道中一行的信道做MRT，然后利用第三节B部分的相位对齐的算法求解IRS的相位，最后算出基站的发射功率P，其代码如下：
% AP-User MRT
function [v_aumrt, w_aumrt] = AUMRT(hd,hr,G)
w_aumrt = hd'/norm(hd);
varphi0 = angle(hd*w_aumrt);
v_aumrt = exp(1j*(varphi0 - angle(diag(hr)*G*w_aumrt)));
end
% AP-IRS MRT
function [v_aimrt, w_aimrt] = AIMRT(hd,hr,G)
w_aimrt = G(1,:)'/norm(G(1,:));
varphi0 = angle(hd*w_aimrt);
v_aimrt = exp(1j*(varphi0 - angle(diag(hr)*G*w_aimrt)));
end交替迭代优化
第三节B部分的算法，给定基站波束方向，优化IRS的相位，计算得到发射功率然后更新基站波束方向，并进行得带，直至收敛，其代码如下：
function [P] = AO(hd,hr,G,epsilon,gamma)
w = hd'/norm(hd); % 论文中说以Ap-user MRT进行初始化
P_new = 0;
P = 10;
while (abs(P-P_new)>epsilon)
varphi0 = angle(hd*w);
v = exp(1j*(varphi0 - angle(diag(hr)*G*w)));
P = P_new;
P_new = gamma/(norm((v.'*(diag(hr)*G)+hd)*w)^2);
w = (v.'*diag(hr)*G+hd)'/norm((v.'*diag(hr)*G+hd));
end
end实验结果
只对实验中单用户系统随着 d 变化的图进行了仿真，其他图可以简单修改主循环进行仿真，得到的仿真图如下
复现得到的
论文原图
可以看出每个算法的走势基本上相似，数值上有一些差距，一是不太清楚作者是如何产生信道G，二是可能有些参数没有对齐，如IRS单元的个数，不过不影响对于算法的理解。
总结
本文对经典的RIS文献的单用户场景进行了复现，并给出了一系列对比方法的复现，结果与论文给出的结果基本相近，通过对该论文的复现，增加了对IRS的理解，以及对比算法的选取。
欢迎大家批评指正，有不清楚的地方欢迎留言或私信交流，希望可以尽快复现出多用户场景的部分。