读论文：深度压缩：用剪枝、训练有素的量化和胡夫曼编码压缩深度神经网络

标题: DEEP COMPRESSION: COMPRESSING DEEP NEURAL NETWORKS WITH PRUNING, TRAINED QUANTIZATION AND HUFFMAN CODING
作者: Song Han、Huizi Mao、William J. Dally

---

Abstract

众所周知，由于神经网络是计算、内存密集型的，所以其对于硬件的需求也不小。而且在本文发布之前，也有其他的研究人员对于压缩神经网络有着不小的研究。为了解决这个问题，文本引入了“深度压缩”的概念，该技术使用修剪、量化以及哈夫曼编码技术，在压缩了神经网络的存储需求的同时也没有特别影响其准确性；

Index Term——compression, pruning, trained quantization, Huffman coding；

---

Introduction

即使深度神经网络已经成为了一种非常强大的计算机视觉任务的技术，但由于大量的权重而消耗了大量的内存。比如，AlexNet Caffemodel超过200MB，而VGG-16 Caffemodel超过500MB。这也阻碍了该技术在移动设备上的部署；
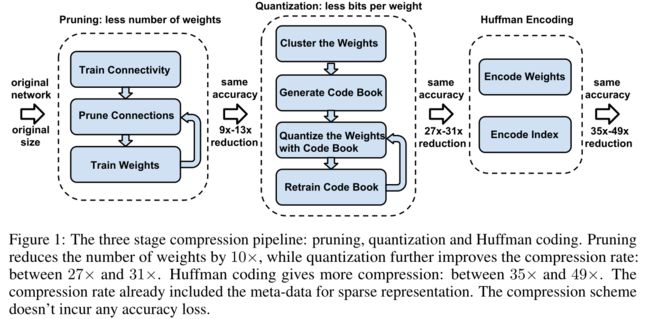
因此，本文的目标就在于减少在大型网络上运行推理所需的存储和能量，以便它们能够被部署在移动设备上。为此，作者提出了“深度压缩”，这是一种分三个阶段的管道：

首先，我们通过去除多余的连接来修剪网络，只保留信息量最大的连接。接下来，对权重进行量化，使多个连接共享相同的权重，因此只需要存储编码本（有效权重）和索引。最后，我们应用哈夫曼编码来利用有效权重的偏向分布。

实行上述方法的理由在于：剪枝和训练有素的量化能够在不互相干扰的情况下压缩网络，从而实现高压缩率；

---

贡献

1. 本文提出了 “深度压缩”，使用该方法能够在不影响精度的前提下极大的压缩了神经网络的大小以及功耗等；
2. 通过该方法，不仅使其在移动端实现的可能性增大了，还有利于在应用大小和下载带宽受到限制的移动应用中使用复杂的神经网络；

---

综述

1. 网络剪枝

就是上面那张图中左边的那部分：首先通过正常的网络训练学习连接性。然后，我们修剪小权重连接：所有权重低于阈值的连接都从网络中删除。最后，我们重新训练网络以学习剩余稀疏连接的最终权重。经过这样的处理，使得AlexNet和VGG-16模型的参数数量分别减少了9倍和13倍；

为了进一步压缩，本文还采用了存储索引差值，如下图所示：

这里以8为例：实际存储的就是与上一个点之间的间隔距离以及其自身的值，当差值超过8时，就在8那里插入一个 填充零 来作为中间人一样的

---

2 训练过的量化和共享权重

此处使用了网络量化（对共享权重进行微调）以及共享权重（让多个连接共享相同的权重）的方法来进一步压缩修剪后的网络。下图说明了共享权重的情况：

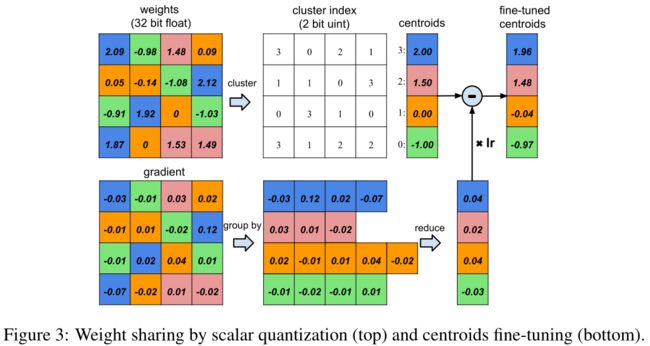
左上方是4×4的权重矩阵，左下方是4×4的梯度矩阵。权重被量化为4个bin（用4种颜色表示），同一bin中的所有权重共享相同的值，因此对于每个权重，我们随后只需要将一个小索引存储到共享权重表中；
在更新过程中，所有的梯度都按颜色分组并相加，乘以学习率，再减去上次迭代的共享中心点；

采用这种方法能够将AlexNet的每个CONV层量化为8位（256个共享权重），每个FC层量化为5位（32个共享权重），而不会损失任何准确性；

压缩率r的计算公式如下：
$$r=\frac{nb}{n{\log }_{a}k+kb}$$

其中，${\log }_{a}k$表示集群数量，n表示连接的网络数量，b表示连接用的位数，k表示共享权重数量

以图三为例，原本有4×4=16个权重，但只有4个共享权重：类似的权重被归为一组，共享相同的值。原来我们需要存储16个权重，每个权重有32位，现在我们只需要存储4个有效的权重（蓝、绿、红、橙），每个权重有32位，再加上16个2位指数，压缩率为$\frac{16\ast 32}{4\ast 32+2\ast 16}=3$

---

2.1 共享权重

本文使用K-Means聚类来确定共享权重。将n个原始权重W = {w₁, w₂, …, w_n}划分为k个簇C = {c₁, c₂, …, c_k}(其中n 》k)，以此来使得簇内平方和（WCSS）最小：$$ar{g}_{C}min\sum _{i=1}^k\sum _{w\in c_i}|w-c_i{|}^2$$

本文的方法是在网络充分训练后确定权重共享，这样共享的权重就接近于原始网络

---

2.2 共享权重的初始化

由于中心点的初始化会影响到聚类的质量，从而影响了预测的精度。本文研究了三种初始化方法：Forgy（随机）、基于密度和线性初始化。以AlexNet中conv3层的原始权重分布（蓝色为CDF，红色为PDF）为例，如下图所示：

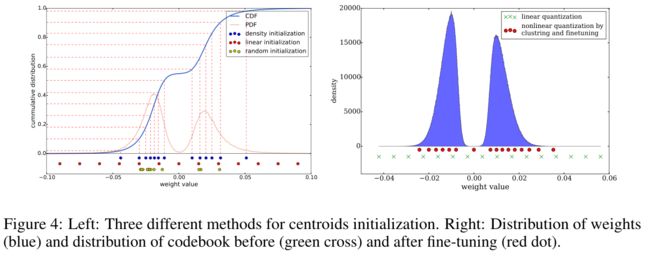
CDF就是PDF的积分。网络修剪后的权重形成了一个双峰分布。底部是3种不同初始化方法下的有效权重（中心点）（以蓝色、红色和黄色显示）。在这个例子中，有13个聚类

• Forgy：从数据集中随机选k个观测值作为初始中心点，图中用黄色点表示，该方法倾向于集中在这两个峰值周围；
• 基于密度分布：在Y轴上初始化线性空间权重的CDF，然后找到与CDF的水平交点，最后在X轴上找到垂直交点，成为一个中心点，如图中蓝点所示。这种方法使中心点在两个峰值周围更密集，但比Forgy方法更散乱；
• 线性分布：再权重空间上进行线性均匀划分。该方法不受权重分布的影响，与前两种方法相比，是最分散的一种；

权重大的点的作用也更大，但是这种点的数量比较少。因此，对于Forgy初始化和基于密度的初始化，很少会出现有代表性的点。后面的实验也表明了线性初始化的效果最好；

---

2.3 前向与反向传播

一维k-means聚类的中心点是共享权重。而在前向与反向传播阶段，会有一个层次的指示来查找权重表，而每个连接都有一个共享权重表的索引。中心点的梯度计算为：$$\frac{\partial L}{\partial C_k}=\sum _{i,j}\frac{\partial L}{\partial W_{ij}}1(I_{ij}=k)$$

其中，L表示损失，用W_ij表示第i列和第j行的权重，用I_ij表示元素Wi,j的中心点指数，用C_k表示该层的第k个中心点。再结合指标函数1(.)来计算中心点的梯度

---

3. 哈夫曼编码

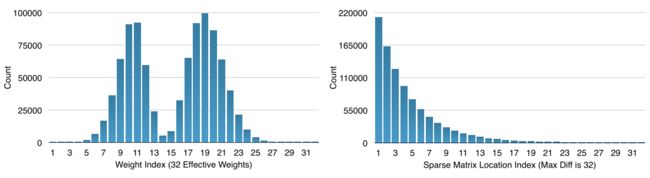
作为一种常用于无损数据压缩的最佳前缀码，该技术也经常被人们所使用。

上图显示了AlexNet中最后一个全连接层的量化权重和稀疏矩阵指数的概率分布。可以看出来，这两个分布都是有偏差的：大部分量化权重都分布在两个峰值附近；稀疏矩阵指数的差值很少超过20。

实验结果表明，对于这些不均匀分布的数据进行哈夫曼编码可以节省2，30%的网络存储；

---

三、实验

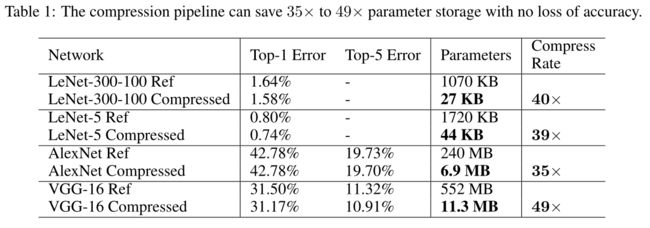
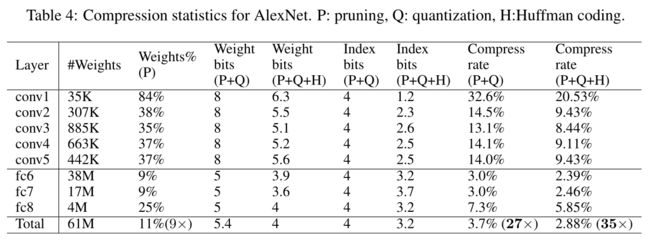
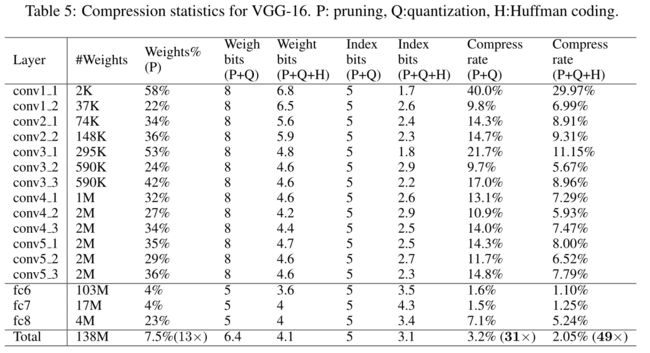
文本分别对两个MNIST和两个ImageNet数据集进行了压缩操作。剪枝前后的参数和准确率如下表所示：

剪枝后的模型不仅节省了35倍到49倍的网络存储量，同时还没有损失准确性

在这次实验当中，训练是用Caffe框架进行的。修剪是通过向点添加一个掩码来实现的，以 掩盖修剪后的连接的更新 。量化和权重共享是通过维护一个存储共享权重的编码簿结构实现的，并在计算每一层的梯度后按索引分组。每个共享权重都会被更新，所有的梯度都会落在这个桶里。哈夫曼编码不需要训练，在所有的微调完成后就可以离线实现

• 对于LeNet模型：
  

• 对于AlexNet模型：它有6100万个参数，取得了57.2%的前1名准确率和80.3%的前5名准确率。经过压缩后的结果如下所示：
  

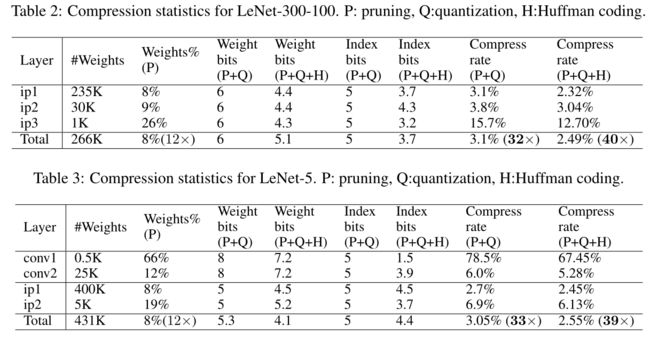
可以看到，AlexNet可以被压缩到其原始大小的2.88%而不影响准确率。每个CONV层有256个共享权重，用8比特编码，每个FC层有32个共享权重，只用5比特编码

• 对于LeNet模型：
  

---

4. 讨论

4.1 剪枝和量化一起

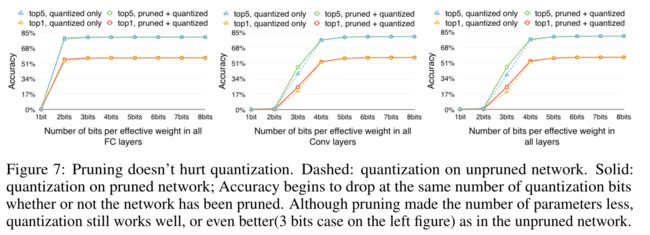
下图显示了在不同的压缩率下，剪枝和量化一起或单独进行的准确性：

不难看出，两者一起进行的压缩表现比起两者单独进行有着十分巨大的提升。绿线代表传统的SVD压缩方法，可以看到其压缩效果十分不好；

上图分别显示了CONV层(左)、FC层(中)和所有层(右)在每个连接的比特数减少时，准确性是如何下降的。虚线只应用量化而没有修剪;实线进行了量化和修剪。两者之间的差别很小。这表明修剪与量化效果很好。前两个图显示CONV层比FC层需要更多的位精度。对于CONV层，精度显著下降到4位以下，而FC层更健壮:直到2位精度才显著下降

此外，量化在经过修剪的网络上工作得很好：因为未经修剪的AlexNet有6000万个权重要量化，而经过修剪的AlexNet只有670万个权重要量化。在质心数量相同的情况下，后者误差较小；

---

4.2 中心点的初始化

下图比较了三种不同初始化方法的精度与top-1精度(左)和top-5精度(右)的关系：

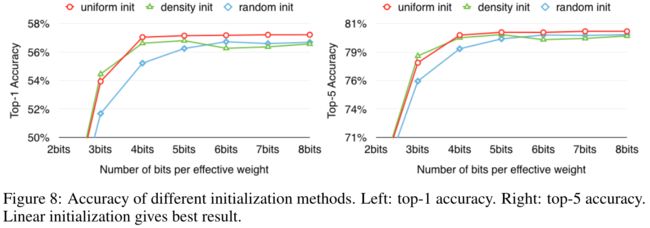
线性初始化在除3位外的所有情况下都优于密度初始化和随机初始化。这是因为线性初始化的初始中心是均匀分布的，而这也有利于保持较大的权重，从而发挥更重要的作用，从而形成较大的质心。这也是另外两种初始化方法无法做到的

---

4.3 加速和能源效率

深度压缩的目标就是为了在移动设备上运行需要实时推理的高度潜伏关注的应用，就比如自动驾驶汽车检测行人的嵌入式处理器一样。
这一节偏硬件，先跳过吧；

---

总结

本文所提出的“深度压缩”能够在不影响准确度的情况来有效的压缩神经网络。经过深度压缩后，这些网络的大小可能会使深度神经网络在移动设备上运行更节能。此外，该压缩方法还有助于在应用程序大小和下载带宽受限的移动应用程序中使用复杂的神经网络。

---

未来展望

尽管裁剪过的网络已经在各种硬件上进行了基准测试，但是由于硬件限制，权重共享的量化网络还能进行同样的测试。因此，适合缓存中的模型的深度压缩的全部优势并没有完全显现出来。对于该问题，有两个解决方案：

1. 软件方面：编写支持该功能的定制GPU内核；
2. 硬件方面：构造定制的ASIC架构，专门用于穿越稀疏和量化的网络结构，它也支持定制的量化位宽；