数字图像处理基础之--像素间的关系(邻接/连通)
图像的像素的意义
一幅图像,经过取样和量化之后就可以得到数字图像。数字图像在存储时,都是由单一的像素保存在存储设备中。像素保存顺序是与像素在数字图片中原本所处在的物理位置相关,那么就要了解像素之间的一些基本关系。
在数字图像处理领域,存在着空间域和变换域的概念。数字图像处理的基本操作,有些需要在空间域中进行,而另外的一些则需要在变换域中进行。
空间域:就是指图像的本身,由所采集到的一个个像素组成。对目标像素进行常用的处理方法,例如灰度变换和空间滤波两大类。
变换域:通过特定的变换函数,将图像的像素变化到目标域中,在变换域中完成相应的操作运算后,再利用反变换核返回到空间域。
由上可知,无论在空间域还是在变换域,像素都是根本。在大多数的数字图像处理中,像素之间在运算时都是要发生关系的,这是因为多个像素构成了图像中的一个对象。
图像是由像素的形式来保存的,所以我们以f(x,y)来表示图像,对于特定像素,分别用p和q来表示。
相邻像素
在这节中主要讨论一个像素p的所有的相邻像素,所有的相邻像素与像素p的距离均不超过√2。.
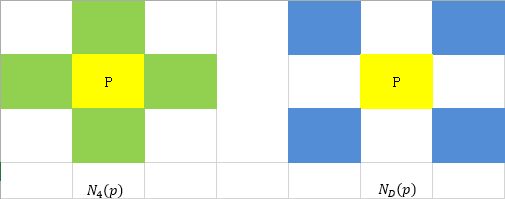
位于坐标(x,y)处的像素p,在水平和垂直方向分别有两个像素与其相邻,对应坐标为:
(x+1,y), (x-1,y), (x,y+1), (x,y-1)
这一组像素称为像素p的4邻域,用N4 ( p)来表示。
对于同样的像素p,在其对角方向有4个像素与其相邻,对应坐标为:
(x-1,y-1), (x-1,y+1), (x+1,y-1), (x+1,y+1)
这一组像素用ND ( p)来表示。
上面的8个坐标点,构成了像素p的8邻域,用N8 ( p)来表示。
在讨论像素点的时候,会遇到这样的情况:像素p位于图像的边界,这样无论是N4 ( p),ND (p ) 都有一些点是不存在的,在目前,讨论这些像素点是没有任何意义。在做特定像素运算的时候,再根据运算的性质来确定如何来处理边界像素的相邻像素。
下图为相邻像素的示意图:
邻接性、连通性
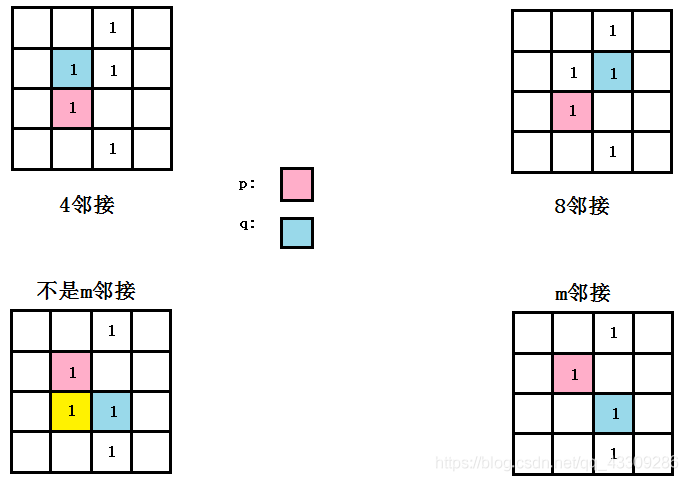
在灰度图像中,假如灰度位数为8bit,那么所有的可能灰度取值范围为[0,255]。为了方便讨论和分析,现只考虑二值图像,即灰度值只有0和1两种情况。定义V为所要讨论的像素的邻接性灰度值集合。则在二值图像中V={1}。分析三种类型的邻接:
4邻接:如果像素q在集合N4 ( p)中,则具有V中灰度值的两个像素q和p是4邻接的。
8邻接:如果像素q在集合N8 ( p)中,则具有V中灰度值的两个像素q和p是8邻接的。
m邻接:如果(1)q在集合N4 ( p)中,或者(2) 像素q在集合ND ( p)中,且集合N4 ( p)∩N4 (q )没有来自V中灰度值的像素,则具有V中数值的两个像素p和q是m邻接的。
对于邻接性,更鲜明扼要的解释如下:
4邻接:像素p q的灰度值属于集合V,像素q在N4( p)中
8邻接:像素p q的灰度值属于集合V,像素q在N8 ( p)中
m邻接:像素p q的灰度值属于集合V,像素q在N4 ( p)中或者像素q在ND §中,且集合N4 ( p)∩N4 ( q)没有来自V中数值的像素。
下图分别给出了4邻接,8邻接,m邻接的示意图。
接下来需要考虑一个问题,在有8邻接后,为什么要引入m邻接的定义呢?在《数字信号处理》2.5.2节中,作者给出的原因是,ml邻接主要是为了消除8邻接的二义性。那么,二义性怎么体现呢?首先来解释什么是像素的通路。
像素的通路
从坐标(x,y)的像素p到坐标为(s,t)的像素q的通路,是由一系列的特定像素组成的序列,其坐标为:
(x0,y0), (x1,y1), …, (xn,yn)
其中(x0,y0) = (x,y), (xn,yn) = (s,t). 并且像素(xi,yi)和(xi-1,yi-1)对于1≤i≤n是邻接的(4邻接,8邻接,m邻接)。在这种情况下,n是通路的长度。从像素p到像素q就形成了一个像素通路。
当按照特定的邻接性来确认像素的通路时,必须保证通路的唯一性,在下图的例子中,如果选择8邻接,则通路并不是唯一的,所以具有二义性。当考虑m邻接的时候,则通路就是唯一的,这就是m邻接可以消除8邻接的二义性体现。
由上图可以看出,在从像素p到像素q的通路中,如果考虑8邻接,那么通路就不具有唯一性。
令S是图像中的一个像素子集,如果S的全部像素之间存在一个通路,则可以说两个像素p和q在S中是连通的。对于S中的任何像素p,S中连通到该像素的像素集成为S的连通分量。如果S仅有一个连通分量,则集合S成为连通集。概括来说,S中的所有的像素,每两个相邻的像素之间是相邻接的(4,8,m),并且只有一个通路,那么S为连通集。
令R是图像中的一个像素子集。如果R是连通集,则R被称作为一个区域。两个区域Ri和Rj如果能形成一个连通集,那么称这两个区域为邻接区域。不过在讨论是否为邻接区域的时候,只能考虑区域边界的像素是否构成4邻接和8邻接,而不考虑m邻接。在定义区域邻接的时候,必须指定邻接类型。
原文链接:https://blog.csdn.net/DdiIcey/article/details/73864470