数字图像处理：像素间的一些基本关系

图像分析的主要目的之一在于获取图像中感兴趣的目标并对目标之间的关系进行分析；目标是由图像中相关像素联合组成的；相关像素在空间的位置和属性都有密切关系，它们一半构成图像中连通组元；所以要分析像素之间的关系，不仅要考虑像素在位置上的联系，还要考虑像素在属性（如灰度）之间的关系。
图像的基本组成单元是像素，像素在图像空间中按照某种规律排列，有一定相互联系。

1 像素间的基本关系

• 像素之间的关系：邻接、连接、连通、通路
• 像素集合之间的关系：邻接、连接、连通

1.1 像素之间的关系：相邻

1.2 像素之间的关系：连接

1.2.1 4-连接

• 两个像素p和r在V中取值，且r在$N_4(p)$中
• r在$N_4(p)$中意味着p也在$N_4(r)$中

1.2.2 8-连接

• 两个像素p和r在V中取值，且r在$N_8(p)$中
• r在$N_8(p)$中意味着p也在$N_8(r)$中

1.2.3 m-连接/混合连接

两个像素p和r在V中取值，且满足下列两个条件之一：

• (1) r在$N_4(p)$中，即两个像素p和r是4-连接；
• (2) r在$N_D(p)$中，且$N_4(p)$)和$N_4(r)$在V的意义下是空集，即$N_4(p)$∩$N_4(r)$不包含V中取值的像素

下面我们主要对第二种条件进行解释，看下面这个例子：

(a)：$r\in N_D(p)$且$N_4(p)\cap N_4(r)=\left\{c,d\right\}$
(b)：设V = {}, 该图满足混合连接的条件。
( c)：设V = {}, 该图不满足混合连接的条件。

m-连接可以认为是8-连接的一种变形，引进它是为了消除使用8-连接时，常出现的多路问题。

看下面这个例子，

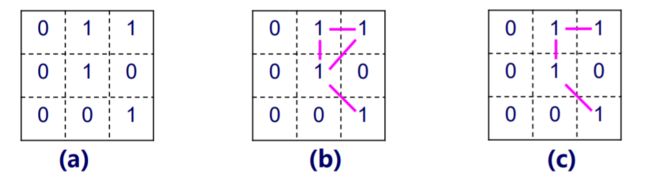
(a) 原始图像。
(b) 设V = {}时的8-连接图像（歧义性，中心像素和右上角像素间存在连线）
( c) 用m-连接消除歧义后的图像（中心像素和右上角像素间的m-连接不能成立）。

注意：

• 4-连接一定是8-连接，也一定是m-连接。
• 混合连接实质上是像素间同时存在4-连接和8-连接时，优先采用4-连接，并屏蔽掉两个和同一像素间存在4-连接的像素之间的8-连接。

1.3 像素之间的关系：邻接与连接

• 邻接：两个像素接触，则它们是邻接的。一个像素和它的邻域中的像素是接触的。邻接仅考虑像素的空间关系。
• 连接：（1）是邻接的，（2）灰度值（或其他属性）满足某个特定的相似准则（灰度相等或灰度在某个集合中，等等）。

1.4 像素之间的关系：像素的通路

• 从具有坐标$(x,y)$的像素$p$到具有坐标$(s,t)$的像素$q$的一条通路由一系列具有坐$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$的独立像素组成，且满足：
  (1) $(x_0,y_0)=(x,y),(x_n,y_n)=(s,t)$
  (2) $(x_i,y_i)$与$(x_{i-1},y_{i-1})$邻接
  (3) $1\le i\le n$，$n$为通路长度。

• 如果 $(x_0,y_0)=(x_n,y_n)$，则通路称为闭合通路

• 根据不同的邻接定义，可以得到不同的通路，如：4-邻接 => 4-通路；8-邻接 => 8-通路

1.4 像素之间的关系：像素的连通

• 像素间的连通：像素和之间的通路上所有像素的灰度值均满足某个特定的相似准则，则像素和是连通的。
• 根据不同的邻接定义，可以得到不同的连通，如
  4-邻接 => 4-连通，8-邻接 => 8-连通
• 连接可以看作是像素连通的一种特例（两个像素）。

1.5 像素集合之间的关系：邻接、连接和连通

像素集合间的邻接：对于两个图像子集和来说，如果中的一个一些像素与 中的一个或一些像素邻接，则可以说两个图像子集和是邻接的。可以说两个图像子集是4-邻接、8-邻接的.

像素集合间的连接：对于两个图像子集和来说，如果中的一个一些像素与 中的一个或一些像素连接，则可以说两个图像子集和是连接的。

像素集合间的连通：设和是一个图像子集中的两个元素，如果存在一条完全由中的像素组成的从和的通路，则称在中与连通。

2 图像的区域的边界

图像里每个连通集，构成图像中的一个区域，图像可以认为是一些列的区域组成。区域的边界也成为区域的轮廓，是该区域的一个子集，但在其邻域中有不属于该区域的像素，它将该区域与其他区域分开。必须指定所用连接类型才能确定一个像素是否属于边界。
看下面这个例子：

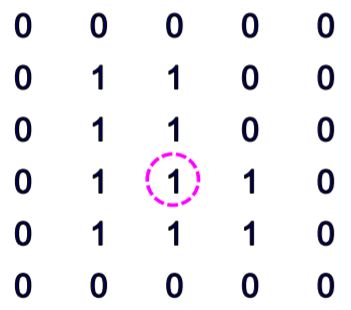
被圈出的点，如果包含1的区域与背景间用8-连接定义连通性，则其属于赋1值区域的边界；如果用4-连接定义连通性，则其就不属于赋1值区域的边界。

3 像素间的距离

像素间的距离指的是测量像素在空间的接近程度。

距离度量函数定义：
设3个像素$p,q,r$，坐标分别为 $(x,y),(s,t),(u,v)$，函数 为一个距离度量函数，其必须满足下列三个条件：

(1) $D(p.q)\ge 0,D(p,q)=0当且仅当p=q$（像素距离非负）

(2) $D(p,q)=D(q,p)$（像素距离与起终点选择无关）

(3) $D(p,r)\le D(p,q)+D(q,r)$（像素之间的最短距离是直线距离）

3.1 欧氏距离$D_E$

范数为2的距离。设像素和的坐标分别为 , 和 ,，它们之间的欧氏距离定义为：
$$D_E(p,q)=\sqrt{(x-s{)}^2+(y-t{)}^2}$$

3.2 城区距离$D_4$

也叫曼哈顿距离，是范数为1的距离.
$$D_4(p,q)=|x-s|+|y-t|$$

3.3 棋盘格距离$D_8$

也叫切比雪夫距离.
$$D_8(p,q)=\max \left\{|x-s|,|y-t|\right\}$$

3.4 $D_m$距离

像素点之间的最短m-通路的长度，其数值依赖于沿m-通路的像素和它们近邻像素的值。看下面这个例子，

其中，$p=1,q=1$.
若$s=0,t=0$，则$D_m(p,q)=2$
若$s=0,t=1$，则$D_m(p,q)=3$
若$s=1,t=0$，则$D_m(p,q)=3$
若$s=1,t=1$，则$D_m(p,q)=4$