【论文学习】On the representation and estimation of spatial uncertainty

Randall C. Smith与Peter Chessman，发表于1987年，这篇文章被认为是最早提出SLAM问题的一篇文章。
CSDN文章链接（欢迎使用积分下载）：https://download.csdn.net/download/tfb760/11888452
百度网盘分享（如果实在没有积分的话）：https://pan.baidu.com/s/1Ys2R5TxKjBLYbuOapqlLjg&shfl=shareset 提取码: 75gv

1. 文章核心思想

当机器人从初始位置进行多次移动时，每次移动对应一个不确定的近似变换（approximate transformation, AT），每次移动后由于不确定性的累加导致不确定性越来越大。文章提出用两个步骤进行精准地估计位置：复合（Compounding）与融合（merging）。

2. 具体方法

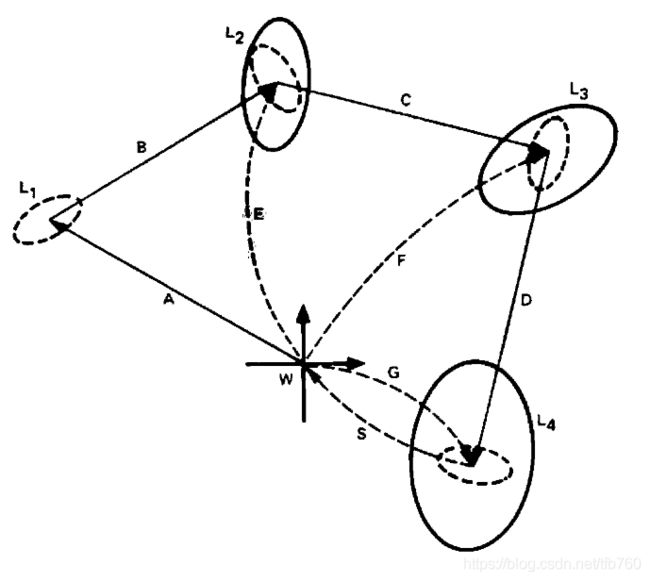
上图示意了机器人的移动，从最初始的W坐标系开始，依次移动到L1,L2,L3,L4。实线ABCD表示相对移动，实线椭圆表示通过相对移动方法计算出的位置的不确定性；虚线EFG表示对应位置测量的对于W的相对移动，虚线椭圆表示直接测量到W的不确定性。S表示G的逆过程。

2.1 复合（Compounding）

对于图中的L2，经过了AB两次运动，定义每次运动时所在的坐标为$(X_i,Y_i,{\theta }_i)$，其中角度$\theta$是当前坐标系对于上一个坐标系的旋转量。可以推导出如下递推公式：
$$X_3=X_2\cos {\theta }_1-Y_2\sin ({\theta }_1)+X_1$$ $$Y_3=X_2\sin {\theta }_1+Y_2\cos {\theta }_1+Y_1$$ $${\theta }_3={\theta }_1+{\theta }_2$$
假设小范围线性，利用泰勒展开，只保留一次项，可以得到坐标系变换
$$(\delta X_3,\delta Y_3,\delta {\theta }_3{)}^T=J\ast (\delta X_1,\delta Y_1,\delta {\theta }_1,\delta X_2,\delta Y_2,\delta {\theta }_2{)}^T$$
其中$J$为雅克比矩阵，为分别对 $X_1,Y_1,{\theta }_1,X_2,Y_2,{\theta }_2$ 进行矩阵求导，从而可以写成：$J=[H|K]$ 形式。
此时不确定度（方差矩阵）可以通过上式进行求2范数，即分别乘以转置，得到新的不确定度：
$$C_3=J(C_1,0;0,C_2)J^T=H{C}_1{H}^T+K{C}_2{K}^T$$

简单解释：第一次和第二次运动没有相关性，所以是个块对角矩阵；

由此得到了方差的合并。从而能够将两次运动复合成一次。

2.2 融合（Merging）

融合是指在测得或计算出相对于W的坐标位置后时，能够测得W对于当前坐标系的位置，即知道逆过程，可以将两个进行融合成一个更为准确的表示，采用了卡尔曼滤波。
设两个表示矩阵分别为 $C_1,C_2$，互为逆过程，则通过以下方式计算合并后的新的不确定性矩阵$C_3$与均值（期望位置）
$$K=C_1\ast [C_1+C_2{]}^{-1}$$ $$C_3=C_1-K\ast C_1$$ $$\widehat{X_3}=X1+K\ast (X_2-X_1)$$
从而融合后获得了更精确的方差矩阵，与新的位置期望。