Policy Gradient (PG)与Proximal Policy Optimization (PPO)算法详解

参考学习课程

David Silver Reinforcement Learning
李宏毅教授强化学习

---

Value-based 与 Policy-based

强化学习可以按照方法学习策略来划分成Value-based和Policy-based两种。而在深度强化学习领域将深度学习与基于值的Q-Learning算法相结合产生了DQN算法，通过经验回放池与目标网络成功的将深度学习算法引入了强化学习算法。其中最具代表性分别是Q-Learning与Policy Gradient算法，将Q-Learning算法与深度学习相结合产生了Deep Q Network，而后又出现了将两种方式的优势结合在一起的更为优秀Actor Critic，DPG, DDPG，A3C，TRPO，PPO等算法。

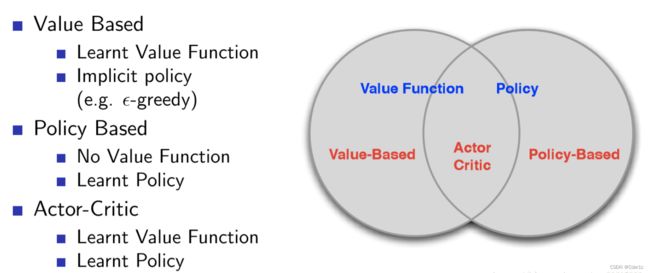
比如，在一个游戏里，目前处于状态s，动作空间A为{a1, a2, a3}，现在要对动作进行选择。

1. Value-based：比较a1, a2, a3三个个动作的期待值（Q-value），选取Q最大的那个作为本次选择的动作。
2. Policy-based：有一个计算此刻选择哪个动作的函数（actor），并得到概率概率p(s,a)，根据概率p(s,a)选取动作。
   
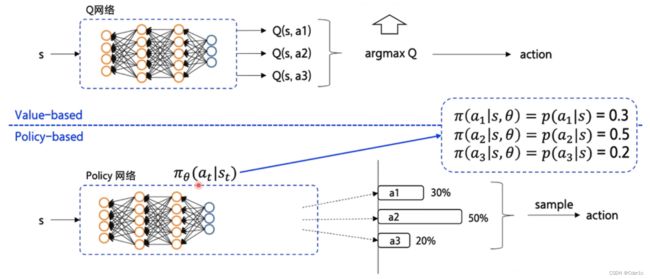
   value-based 的典型算法是DQN，policy-based是policy gradient

Policy Gradient (PG)

基本原理

在强化学习中，环境与reward function是不能控制的，你所能改的只有actor，也就是玩家的经验策略。
对于 Policy Based 强化学习方法下，Actor就是训练的模型，也就是玩家，是一个使用参数$\theta$近似的${\pi }_{\theta }(s,a)$，然后找出最好的$\theta$。

这里是李宏毅教授视频中的一个例子：
机器先观察画面，然后做出了一个action，向right移动，这个action的奖励是$r_1=0$，然后机器又观察画面，做出了fire的action，然后观察画面，发现有外星人被击落，然后获得reward $r_2=5$。

经过很多轮$(s,a,r)$，游戏结束了。从游戏开始到游戏结束被称为一个episode，将每一个episode的 reward 相加就能得到Total reward: $R={\sum }_{t=1}^T{r}_t$ 。我们希望通过训练更好的acrtor使得R可以尽可能的大。

把每一个episode的所有s和a的序列放在一起，就是Trajectory

通过以上可得知 $\pi$在参数为$\theta$情况下时$\tau$发生的概率为：
$$\begin{gathered} p_{\theta }(\tau ) \\ =p(s_1)p_{\theta }(a_1|s_1)p(s_2|s_1,a_1)p_{\theta }(a_2|s_2)p(s_3|s_2,a_2)... \\ =p(s_1){\prod }_{t=1}^T{p}_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t) \end{gathered}$$

得到了概率之后我们就可以根据采样得到的回报值计算出数学期望:
$\overline{R_{\theta }}={\sum }_{\tau }{p}_{\theta }(\tau )R_{\tau }=E_{\tau \sim p_{\theta }(\tau )}[R_{\tau }]$

为了使$\overline{R_{\theta }}$最大化，我们需要做gradient ascent：

1. 由于$E_{\tau \sim p_{\theta }(\tau )}[R_{\tau }{p}_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )]$是无法计算的，所以我们sample出N个$\tau$，对每个$\tau$取$R_{\tau }{p}_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )$，并求和取平均
2. 将$R_{{\tau }^{(}n)}\nabla log{p}_{\theta }({\tau }^n)$写为${\sum }_{t=1}^{T^n}{R}_{{\tau }^{(}n)}\nabla log{p}_{\theta }(a_t^n|s_t^n)$

观察最后的$\frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T^n}{R}_{{\tau }^{(}n)}\nabla log{p}_{\theta }(a_t^n|s_t^n)$，如果在$s_t^n$下执行$a_t^n$得到的$R_{{\tau }^{(}n)}$为正，则增加这个选择的概率，否则减少概率

在实际实验中，我们会让actor去和environment做互动，产生左边的数据。左边的方框是做sample，获得很多$(s,a)$ 的pair（代表在s下采取a，得到 $R(\tau )$ ），然后将这些数据送入训练过程中计算$\nabla log{p}_{\theta }(a_t^n|s_t^n)$，并更新模型的参数$\theta$。

PG的两个小技巧

1. Add a baseline
   
   比如，在ideal case的第一张图，a和c的会使总的奖励变多，那么机器会倾向于执行a和c的操作，所以a和c的执行几率就变大了，相对的b的几率就减少了。然后我们再看看sampling那一行，b和c可能使我的总的奖励一直是正的，那么机器根本就不知道a的情况，万一a的操作更好呢？？机器只会去学更positive的，b和c的几率也会越来越大，a只会越来越小。这时，我们需要引入一个baseline，将总的奖励减去一个b值，也就是某一步的奖励一定要达到某一个标准我才能说它好，否则就是不好。通常我们可以将这个b设为与$R(\tau )$的期望接近的值。

2. Assign suitable credit
   比如下面是一个简单的游戏，就三步，第一组(s,a)得到的奖励是+5，第二组是0，第三组是-2，然后最后的奖励是+3,如果我们用之前的那个损失函数，那么就默认了每一个(s,a)的组合的权重都是+3,这显然是不靠谱的，虽然总的奖励是正的，但是明显里面有些组合不靠谱，我们就可以给那些不靠谱的组合负的权重。于是我们将$R({\tau }^n)$换成下图的样子。这样就可以对每一个组合的权重加以区分。
   
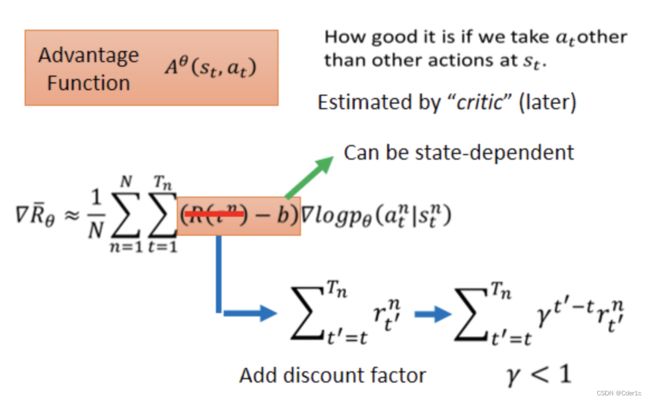
   同时，我们再增加一个衰减因子$\gamma$，意味着随着时间推移，组合越来越多，那么前面的组合对很后面的组合的影响就越来越小。然后我们将红框框住的那部分重新命名一个函数，叫Advantage function

Proximal Policy Optimization (PPO)

PG的不足

1. 采样效率低
   PG采用MC采样方式，每次基于当前的策略对环境采样一个episode数据，然后基于这些数据更新策略，这个过程中数据仅仅被利用了一次就扔掉了，相比于DQN等离线学习算法，PG这种更新方式是对数据的极大浪费。
2. 训练不稳定
   在强化学习中当前的动作选择会影响到将来的情况，不像监督学习的训练样本是相互独立的，如果某一批次的样本不好导致模型训练的很差，只要其他的训练数据没问题最终也能得到一个好的结果。但是在PG中，对于某次策略更新的太大或者太小，就会得到一个不好的Policy，一个不好的和环境交互就会得到一个不好的数据，用这些不好的数据更新的策略很大概率也是不好的。所以训练时候会有下图这种情况，训练过程中会忽然进入一个很差的状态。

On-policy 和 Off-policy

1. On-Policy方式指的是用于学习的agent与观察环境的agent是同一个，所以参数$\theta$始终保持一致。
2. Off-Policy方式指的是用于学习的agent与用于观察环境的agent不是同一个，他们的参数$\theta$可能不一样。

基本原理

在PG中，下图蓝线画的部分，表示的是在某个actor的情况下，或者说是某个参数θ的情况下，随机取样出来不同的$\tau$的期望，然后我们利用梯度上升更新$\theta$，但是$\theta$只要一更新，这个期望就会变，也就是说当$\theta$更新时，我们又必须重新计算期望。

在PPO中，使用Off-Policy能解决这个问题，我们使用${\pi }_{{\theta }^{\prime }}$去和环境做互动，我们可以得到在${\theta }^{\prime }$下所随机取出的样本的期望，然后让${\pi }_{\theta }$去利用这个这些样本去训练$\theta$。

Importance Sampling：
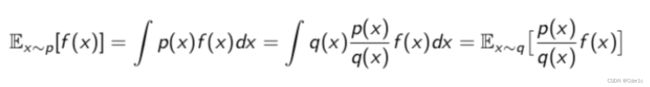我们要求$f(x)$的期望，其中$x$服从$p(x)$分布，可以通过变换，$x$可以从另外一个分布$q(x)$中采样，这时$f(x)$就需要乘上一个重要性权重$\frac{p(x)}{q(x)}$。通过这种方式就可以从另外一个分布采样来计算原式，后面只需要乘上一个重要性权重就可以了。

回到PPO中，PG是model-free的所以不知道模型的概率，所以只能通过与真实环境数据的分布$P(x)$中去采样加和平均求期望。但现在我们为了把它变成off-policy，就不能直接从$P(x)$中去直接采样。然后使用Importance Sampling，可以把原来$x\sim p$的期望改写成$x\sim q$的期望。

PG中策略更新梯度为：$\nabla R_{\theta }=E_{\tau \sim p_{\theta }(\tau )}[R_{\tau }{p}_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )]$，而PPO中的策略更新梯度为：$\nabla R_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}{R}_{\tau }{p}_{\theta }(\tau )\nabla log{p}_{\theta }(\tau )]$

如果采样的分布$p$与真实的分布$q$差得很多，那么肯定会导致两个期望不一致。

先看等式左半边，在$p$里面取$x$，那么$p$的左半边被取的机率很高，然后左半边又都是正的，然后代入$f(x)$,但是$f(x)$的左边都是负的，所以整个期望是负的。然后再看等式右边，在$q$里面取，$q$在右边被取得几率大，然后$q$大于$p$，所以$\frac{p}{q}$小于1，然后$f(x)$又是正的，所以为正，但事实果真如此吗？如果我现在sample到了一个左边的点，$f(x)$就为负了，而且$\frac{p}{q}>1$,这将影响整个右边的结果，可能为负，所以只有在取更多样本时，下面这个式子才越准确。

同时，最后方差的式子是不一样的，多了红框圈出的部分，也说明p与q不能差距太大。
我们希望能想办法约束$\theta$与${\theta }^{\prime }$的差距不要过大，使用KL散度也叫相对熵，可以用来衡量两个分布之间的差异性。

1. 最直接的办法，就是对目标函数增加一个约束条件让他的KL散度小于$\delta$。也就Trust Region Policy Optimization (TRPO)
   $$\begin{gathered} \nabla R_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}{A}^{{\theta }^{\prime }}(s,a)] \\ KL(\theta ,{\theta }^{\prime })<\delta \end{gathered}$$

2. 但是直接求解TRPO这种带约束的问题是十分复杂的，PPO1将KL散度作为惩罚项，更加容易求解。
   $$\begin{gathered} \nabla R_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}{A}^{{\theta }^{\prime }}(s,a)]-\beta KL(\theta ,{\theta }^{\prime }) \\ ={\sum }_{(s_t,a_t)}\frac{p_{\theta }(s_t,a_t))}{p_{{\theta }^{\prime }}(s_t,a_t))}{A}^{{\theta }^{\prime }}(s_t,a_t)-\beta KL(\theta ,{\theta }^{\prime }) \end{gathered}$$

3. 另外还有一种PPO2算法效果比PPO要好一些
   $\nabla R_{\theta }={\sum }_{(s_t,a_t)}min(\frac{p_{\theta }(s_t,a_t))}{p_{{\theta }^{\prime }}(s_t,a_t))}{A}^{{\theta }^{\prime }}(s_t,a_t),clip(\frac{p_{\theta }(s_t,a_t))}{p_{{\theta }^{\prime }}(s_t,a_t))},1-ϵ,1+ϵ)A^{{\theta }^{\prime }}(s_t,a_t))$

利用clip函数将其固定在了一定的范围之内，同样也可以起到限制约束$\theta$与${\theta }^{\prime }$的作用。