详解自注意力机制及其在LSTM中的应用
详解自注意力机制及其在LSTM中的应用
注意力机制(Attention Mechanism)最早出现在上世纪90年代,应用于计算机视觉领域。2014年,谷歌Mnih V等人[1] 在图像分类中将注意力机制融合至RNN中,取得了令人瞩目的成绩,随后注意力机制也开始在深度学习领域受到广泛关注,在自然语言处理领域,Bahdanau等人[2] 将注意力机制融合至编码-解码器中,在翻译任务取得不错的效果。而真正让注意力机制大火的是2017年,谷歌提出的Transformer[3],它提出了自注意力机制(self-Attention Mechanism),摒弃了RNN和CNN,充分挖掘了DNN的特性,刷新了11项NLP任务的精度,震惊了深度学习领域。
注意力机制基于人类的视觉注意力,人在观察物体的时候往往会把重点放在部分特征上,注意力机制就是根据这个特点,基于我们的目标,给强特征给予更大的权重,而弱特征给予较小权重,甚至0权重。
文章目录
-
- 详解自注意力机制及其在LSTM中的应用
- 1.注意力机制本质
- 2.自注意力机制
- 3.多头自注意力
- 4.(多头)自注意力机制在LSTM中的应用
- 5.结语
1.注意力机制本质
注意力机制(Attention Mechanism)的本质是:对于给定目标,通过生成一个权重系数对输入进行加权求和,来识别输入中哪些特征对于目标是重要的,哪些特征是不重要的;
为了实现注意力机制,我们将输入的原始数据看作< Key, Value>键值对的形式,根据给定的任务目标中的查询值 Query 计算 Key 与 Query 之间的相似系数,可以得到Value值对应的权重系数, 之后再用权重系数对 Value 值进行加权求和, 即可得到输出。我们使用Q,K,V分别表示Query, Key和Value,注意力权重系数W的公式如下:
W = s o f t m a x ( Q K T ) W =softmax(QK^T ) W=softmax(QKT)
将注意力权重系数W与Value做点积操作(加权求和)得到融合了注意力的输出:
A t t e n t i o n ( Q , K , V ) = W ⋅ V = s o f t m a x ( Q K T ) ⋅ V Attention(Q,K,V) = W·V=softmax(QK^T )·V Attention(Q,K,V)=W⋅V=softmax(QKT)⋅V
注意力模型的详细结构如下图所示:
需要注意,如果Value是向量的话,加权求和的过程中是对向量进行加权,最后得到的输出也是一个向量。
可以看到,注意力机制可以通过对< Key, Query>的计算来形成一个注意力权重向量,然后对Value进行加权求和得到融合了注意力的全新输出,注意力机制在深度学习各个领域都有很多的应用。不过需要注意的是,注意力并不是一个统一的模型,它只是一个机制,在不同的应用领域,Query, Key和Value有不同的来源方式,也就是说不同领域有不同的实现方法。
2.自注意力机制
自注意力机制(self-Attention Mechanism),它最早由谷歌团队[34]在2017年提出,并应用于Transformer语言模型。自注意力机制可以在编码或解码中单独使用,相对于注意力机制,它更关注输入内部的联系,区别就是Q,K和V来自同一个数据源,也就是说Q,K和V由同一个矩阵通过不同的线性变换而来。
比如对于文本矩阵来说,利用自注意力机制可以实现文本内各词“互相注意”,即词与词之间产生注意力权重矩阵,然后对Value加权求和产生一个融合了自注意力的新文本矩阵。文本自注意力的实现步骤如下:
- 假设文本矩阵 i n p u t = R ( a × b ) input=R^{(a×b)} input=R(a×b),三个变换矩阵(卷积核): ω q , ω k ∈ R ( b × d ) 、 ω v ∈ R ( b × c ) ω^q,ω^k∈ R^{(b×d)}、ω^v∈ R^{(b×c)} ωq,ωk∈R(b×d)、ωv∈R(b×c);
- Q、K、V变换:文本矩阵和三个权重矩阵做线性变换,得到 Q , K ∈ R ( a × d ) 、 V ∈ R ( a × c ) Q,K∈ R^{(a×d)}、V∈ R^{(a×c)} Q,K∈R(a×d)、V∈R(a×c):
Q = i n p u t ω q , K = i n p u t ω k , V = i n p u t ω v Q =input ω^q, K =input ω^k, V =input ω^v Q=inputωq,K=inputωk,V=inputωv - 缩放点积: Q × K T Q×K^T Q×KT然后乘以一个 1 / d k 1/\sqrt{d_k} 1/dk( d k d_k dk为K的维度, 1 / d k 1/\sqrt{d_k} 1/dk为缩放因子,防止内积数值过大影响神经网络的学习),得到注意力得分矩阵 G ∈ R ( a × a ) G∈ R^{(a×a)} G∈R(a×a),G的行表示某个词在各个词上的得分:
G = Q K T / d k G =QK^T/\sqrt{d_k} G=QKT/dk - 得到注意力权重矩阵: s o f t m a x ( G ) softmax(G) softmax(G)表示注意力权重矩阵W :
W = s o f t m a x ( ( Q K T ) / d k ) W=softmax((QK^T)/\sqrt{d_k}) W=softmax((QKT)/dk) - 得到结果矩阵: W* V 得到一个结果矩阵Attention∈ R^(a×c),该矩阵就是一个全新的融合了注意力机制的文本矩阵z:
z = A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T / d k ) V z=Attention(Q,K,V) =softmax(QK^T/\sqrt{d_k})V z=Attention(Q,K,V)=softmax(QKT/dk)V
在上述公式中,变换矩阵 ω q 、 ω k 、 ω v ω^q、ω^k、ω^v ωq、ωk、ωv都是神经网络的参数,可以随着反向传播而修改,通过修改这些变换矩阵来达到自注意力转移的目的。
3.多头自注意力
若为多头自注意力机制,则有多组卷积核 ω i q , ω i v , ω i k ω_i^q,ω_i^v,ω_i^k ωiq,ωiv,ωik,将步骤2-5进行h次得到h组结果矩阵 ( z 1 , . . . , z h ) (z_1,...,z_h ) (z1,...,zh),将 ( z 1 , . . . , z h ) (z_1,...,z_h ) (z1,...,zh)拼接并做一次线性变换 ω z ω^z ωz就得到了我们想要的文本矩阵:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( z 1 , . . . , z h ) ω z MultiHead(Q,K,V )= Concat(z_1,...,z_h ) ω^z MultiHead(Q,K,V)=Concat(z1,...,zh)ωz
缩放点积计算和多头自注意力机制计算过程如下图:
自注意力机制将文本输入视为一个矩阵,没有考虑文本序列信息,例如将K、V按行打乱,那么计算之后的结果是一样的,但是文本的序列是包含大量信息的,比如“虽然他很坏,但是我喜欢他”、“虽然我喜欢他,但是他很坏”,这是两个极性相反的句子,因此需要提取输入的相对或绝对的位置信息。
Positional Encoding计算公式如下:
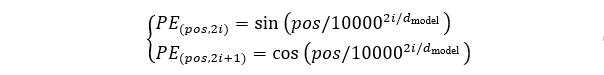
式中,pos 表示位置index,i表示位置嵌入index。
得到位置编码后将原来的word embedding和Positional Encoding拼接形成最终的embedding作为多头自注意力计算的输入input embedding。
4.(多头)自注意力机制在LSTM中的应用
LSTM包含两个输出:
- 所有时间步输出 O = [ O 1 , O 2 , … , O D ] O= [O_1,O_2,…,O_D] O=[O1,O2,…,OD]
- 最后时间步D的隐藏状态 H D H_D HD
由于 O = [ O 1 , O 2 , … , O D ] O= [O_1,O_2,…,O_D] O=[O1,O2,…,OD]表示字/词的特征, H D H_D HD表示文本的特征,为了识别字对于文本的重要性,我们需要建立 H D H_D HD与 O O O的自注意力关系,即建立各时间步输出 O t O_t Ot对于 H D H_D HD的权重,由于LSTM本身就考虑了位置信息,因此不需要额外设置位置编码,自注意力机制在LSTM中的实现方法有两种:
1. 点积注意力[2]:Transfromer提出的自注意力实现方法
各时间步的输出 O t O_t Ot经线性变换后作为Key和Value,最后时间步的输出 H D H_D HD乘以矩阵 ω Q ω_Q ωQ作为Query。
在时间步t时, K e y t , V a l u e t , Q u e r y , 得 分 e t 和 权 重 a t Key_t,Value_t,Query,得分e_t和权重a_t Keyt,Valuet,Query,得分et和权重at有如下计算公式:

式中,Query不随时间步而改变, ω K , ω Q , ω V ω_K,ω_Q,ω_V ωK,ωQ,ωV是神经网络的参数,随反向传播而修改。将各时间步权重 a t a_t at与 V a l u e t Value_t Valuet加权求和,得到带有自注意力的文本向量:

为了获取多头自注意力,将上述公式进行h次,得到多头自注意力文本 z 1 , . . . , z h z_1,...,z_h z1,...,zh,将其拼接并做一次线性变换后作为最后输出:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( z 1 , . . . , z h ) ω z MultiHead(Q,K,V)= Concat(z_1,...,z_h ) ω_z MultiHead(Q,K,V)=Concat(z1,...,zh)ωz
式中,h为自注意力的头数,多头自注意力结构如下图:
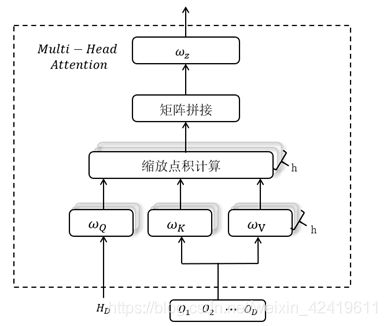
点积注意力Pytorch源码:
self.w_q = nn.Linear(ARGS.hidden_dim * (ARGS.bidirect + 1) * ARGS.n_layers, ARGS.dim_k, bias=False)
self.w_k = nn.Linear((ARGS.bidirect + 1) * ARGS.hidden_dim, ARGS.dim_k, bias=False)
self.w_v = nn.ModuleList([
nn.Linear((ARGS.bidirect + 1) * ARGS.hidden_dim, ARGS.dim_v, bias=False)
for _ in range(ARGS.num_heads)
])
self.w_z2 = nn.Linear(ARGS.num_heads * ARGS.dim_v, ARGS.dim_v, bias=False)
def MultiAttention1(self, lstm_out, h_n):
batch_size, Doc_size, dim = lstm_out.shape
x = []
for i in range(h_n.size(0)):
x.append(h_n[i, :, :])
hidden = torch.cat(x, dim=-1)
dk = ARGS.dim_k // ARGS.num_heads # dim_k of each head
q_n = self.w_q(hidden).reshape(batch_size, ARGS.num_heads, dk).unsqueeze(dim=-1)
key = self.w_k(lstm_out).reshape(batch_size, Doc_size, ARGS.num_heads, dk).transpose(1, 2)
value = [wv(lstm_out).transpose(1, 2) for wv in self.w_v] # value: n* [batch_size, dim_v, Doc_size]
weights = torch.matmul(key, q_n).transpose(0, 1) / sqrt(dk) # weights: [n, batch_size, Doc_size, 1]
soft_weights = F.softmax(weights, 2)
out = [torch.matmul(v, w).squeeze() for v,w in zip(value,soft_weights)]
# out[i]:[batch_size, dim_v, Doc_size] × [batch_size, Doc_size, 1] -> [batch_size, dim_v]
# out: [batch_size, dim] * n
out = torch.cat(out, dim=-1)
out = self.w_z2(out)
return out, soft_weights.data # out : [batch_size, dim_v]
2. 加法注意力[3]:Bahdanau 提出的加法注意力
将最后时间步的隐藏状态 H D H_D HD和各时间步输出 O t O_t Ot拼接作为Query,各时间步输出 O t O_t Ot线性变换后作为Value,线性变换矩阵 ω k ω_k ωk作为Key,Query和Value相乘后作为结果矩阵z,时刻t有如下公式:
Q t = ω q ( O t + H D ) Q_t=ω_q(O_t+H_D) Qt=ωq(Ot+HD)
V t = ω v O t V_t=ω_vO_t Vt=ωvOt
z t = t a n h ( Q t ω k ) V t z_t=tanh(Q_tω_k)V_t zt=tanh(Qtωk)Vt
结果矩阵为 z = [ z 1 , z 2 , . . . , z t , . . . , z D ] z=[z_1,z_2,...,z_t,...,z_D] z=[z1,z2,...,zt,...,zD]
若为多头自注意力,则进行h次操作后获得多个结果矩阵后拼接再做一次线性变换作为输出,如下图:
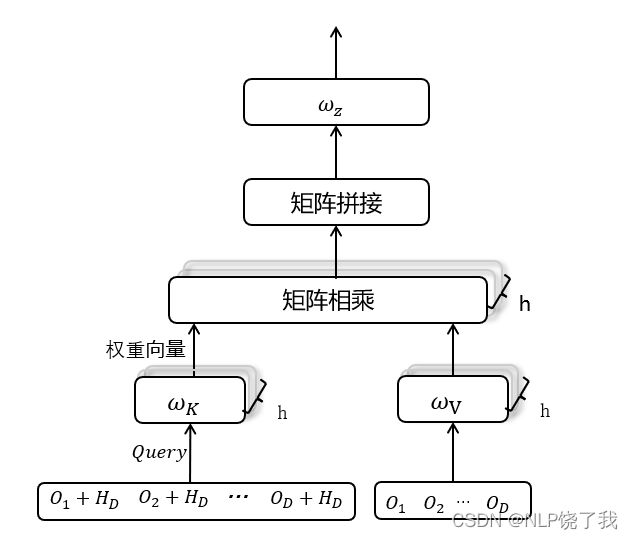
加法注意力Pytorch源码:
self.w_v = nn.ModuleList([
nn.Linear((ARGS.bidirect + 1) * ARGS.hidden_dim, ARGS.dim_v, bias=False)
for _ in range(ARGS.num_heads)
])
self.w_z = nn.Linear(ARGS.num_heads * ARGS.dim_v, ARGS.dim_v, bias=False)
self.w_q = nn.Linear((ARGS.bidirect + 1) * ARGS.hidden_dim * (ARGS.n_layers + 1), ARGS.dim_k, bias=True)
self.w_k_Mul = nn.Linear(ARGS.dim_k // ARGS.num_heads, 1, bias=False)
def MultiAttention4(self, lstm_out, h_n):
batch_size, Doc_size, dim = lstm_out.shape
x = []
for i in range(h_n.size(0)):
x.append(h_n[i, :, :])
hidden = torch.cat(x, dim=-1).unsqueeze(dim=-1)
ones = torch.ones(batch_size, 1, Doc_size).to(device)
hidden = torch.bmm(hidden, ones).transpose(1, 2)
# 对lstm_out和hidden进行concat
h_i = torch.cat((lstm_out, hidden), dim=-1)
dk = ARGS.dim_k // ARGS.num_heads # dim_k of each head
# 分头,即,将h_i和权值矩阵w_q相乘的结果按列均分为n份,纬度变化如下:
# [batch_size, Doc_size, num_directions*hidden_dim*(1+n_layer)] -> [batch_size, Doc_size, dim_k]
# ->[batch_size, Doc_size, n, dk] -> [batch_size, n, Doc_size, dk]
query = self.w_q(h_i).reshape(batch_size, Doc_size, ARGS.num_heads, dk).transpose(1, 2)
query = torch.tanh(query) # query: [batch_size, n, Doc_size, dk]
# 各头分别乘以不同的key,纬度变化如下:
# [batch_size, n, Doc_size, dk] * [batch_size, n, dk, 1]
# -> [batch_size, n, Doc_size, 1] -> [batch_size, n, Doc_size]
weights = self.w_k_Mul(query).transpose(0, 1) / sqrt(dk) # weights: [n, batch_size, Doc_size, 1]
value = [wv(lstm_out).transpose(1, 2) for wv in self.w_v] # value: n* [batch_size, dim_v, Doc_size]
soft_weights = F.softmax(weights, 2)
# value:[batch_size, dim, Doc_size]
out = [torch.matmul(v, w).squeeze() for v, w in zip(value, soft_weights)]
# out[i]:[batch_size, dim, Doc_size] × [batch_size, Doc_size, 1] -> [batch_size, dim]
# out: [batch_size, dim] * n
out = torch.cat(out, dim=-1)
# out: [batch_size, dim * n]
# print(out.size())
out = self.w_z(out) # 做一次线性变换,进一步提取特征
return out, soft_weights.data # out : [batch_size, hidden_dim * num_directions]
Transformer中指出,在高维度的情况下加法注意力的精度优于点积注意力,但是可以通过乘以缩放因子 1 / d k 1/\sqrt{d_k} 1/dk抵消这种影响:
以下是论文[2]的3.2.1小节的原文翻译:
最常用的两个注意力函数是加法注意力[3]和点积(多重复制)注意力。点积注意与我们的算法相同,只是比例因子为 1 / d k 1/\sqrt{d_k} 1/dk。加法注意力利用一个具有单个隐层的前馈网络来计算相容函数。虽然两者在理论复杂度上相似,但由于可以使用高度优化的矩阵乘法码来实现,因此在实践中,点积注意力速度更快,空间效率更高。
对于较小的 d k d_k dk,这两种机制效果相近,对于较大的 d k d_k dk值,加法注意力优于点积注意力。我们怀疑,对于较大的 d k d_k dk值,点积在数量级上增长很大,从而将softmax函数推到梯度非常小的区域。为了抵消这种影响,我们将点积缩放 1 / d k 1/\sqrt{d_k} 1/dk。
5.结语
本文内容主要参考自下述三篇论文以及知乎博文,并对其进行理解和整理。本人也并未完全掌握自注意力机制,想要完全掌握自注意力机制建议阅读这三篇论文的原文。
有错误欢迎指正!
需要源码可私信我哦^ ^
[1] Mnih V, Heess N, Graves A, et al. Recurrent Models of Visual Attention. arXiv preprint, arXiv: 1406.6247 [ cs. CL] 2014.
[2] Vaswani A, Attention Is All You Need, arXiv preprint, arXiv: 1706.03762 [cs.CL] 2017.
[3] Bahdanau D, Cho K, Bengio Y. Neural Machine Translation by Jointly Learning to Align and Translate[J]. Computer Science, 2014.

