KGCN论文阅读
KGCN论文阅读
- KGCN 知识图谱+图神经网络在推荐系统中的应用
-
- 推荐算法的先验知识
- KGCN
-
- 基于知识图谱的推荐系统的问题定义
-
- 定义
- 一些说明
- 整体框架
- 单层KGCN
- 实验
-
- 消融
KGCN 知识图谱+图神经网络在推荐系统中的应用
推荐算法的先验知识
推荐系统中用户中有两种行为,成为显示反馈与隐形反馈。
显示反馈的行为是指用户明显地表达自己的喜好,如喜欢/不喜欢
隐式反馈是指用户不明确表达出自己的喜好信息,如是否点击某个商品。
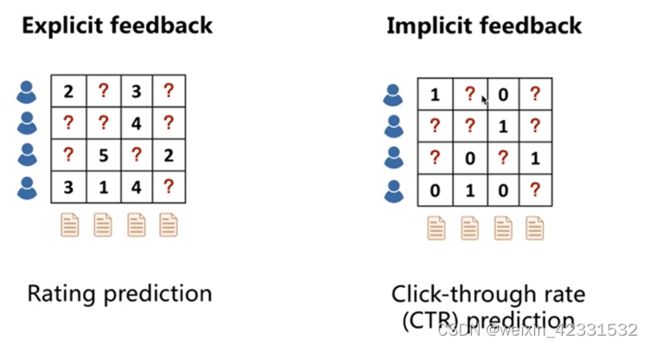
举例:右边是显示表达的例子。一个矩阵,行是user 列是item。每一个用户都对商品进行打分,分越高说明用户对item越喜欢。左边是隐式表达。只有0-1,0表示用户没点击浏览商品,1表示点击了。
推荐系统最经典的是协同过滤算法。它基于一个假设:相似的用户有着相似的喜好。
举个例子进行说明:
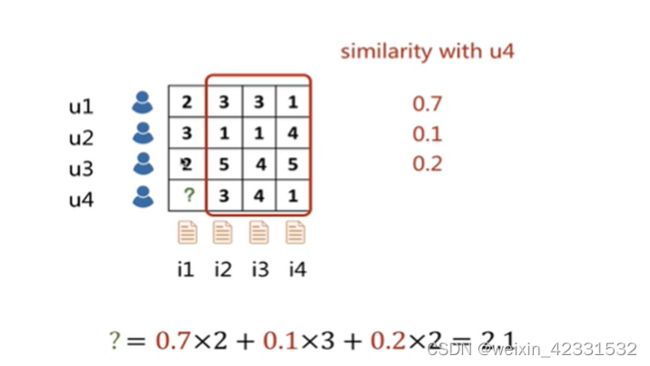
给定一个矩阵,我们要计算u4对与i1的喜欢程度。首先计算u4和其他用户的相似度。依据就是用户对于其他item的打分。我们可以看到,u4和u1对于其他item的是很相似的,所以u4和u1的相似度很高。得到相似度之后,依据u1 u2 u3 对于i1的打分预测u4对i1的打分。
但是协同过滤算法存在两个问题:
1.稀疏性,用户显示地表明对某个item的偏好的信息是非常少的,隐式的信息也不会多,没有数据怎么计算用户的相似度呢?
2. 存在冷启动的问题:就是说缺少用户的历史记录,无法进行推荐。
总之就是说,矩阵有很多空白,信息太少,无法计算。如下图所示
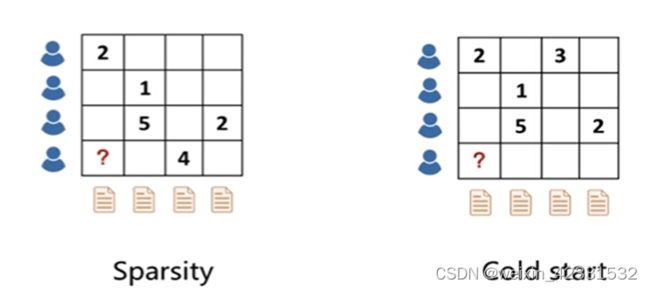
那么如何解决呢?
想法:充分利用user-item的属性信息,引入语义信息。由此提出KGCN
KGCN
优点:端到端模型
2.通过感受野捕捉entity的邻域信息,且感受野可以扩展到高阶,以获得用户的远距离兴趣(图神经网络的性质,每一层聚合一阶邻域的信息,但是可以通过堆叠多层来扩大感受野)
基于知识图谱的推荐系统的问题定义
定义
给定交互矩阵 Y ∈ R M × N Y\in\mathbb{R}^{M\times N} Y∈RM×N和知识图谱 G = ( h , r , t ) G=\left(h,r,t\right) G=(h,r,t). 其中 M是user,N是item 图谱中 h是头实体,r是关系,t是尾实体。预测结果是 y ^ u , v = F ( u , v ∣ θ , Y , G ) {\widehat y}_{u,v}=F(u,v\vert\theta,Y,G) y u,v=F(u,v∣θ,Y,G) 表明u对item v感兴趣的概率有多大。
一些说明
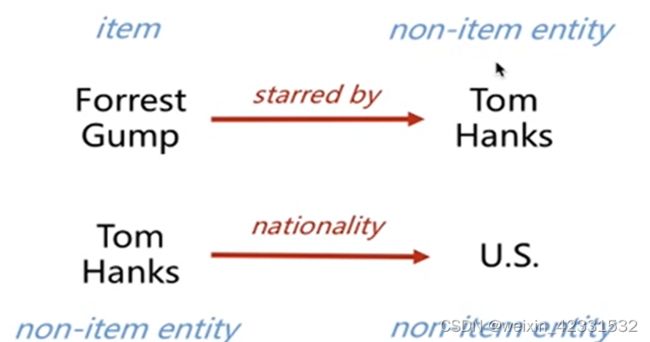
user不属于entity 但是item属于entity。 entity 不一定是 item。 user和 item的关系是interaction, entity与entity之间的关系是relation。可以从下图看到 《阿甘正传》由汤姆汉克斯主演,《阿甘正传》是我们要关注的item,但是汤姆汉克斯不是。汤姆汉克斯的国家是美国,这俩都不是我们要关注的item。
为什么要说这些,因为我们需要的是user和item之间的关系,而不是 entity和entity之间的关系。图里的这些关系是在知识图谱里存在的。我们是在图谱里对item进行特征提取,但是最终得到的是user和item的interaction。
整体框架
有了以上的认知,我们先看一下KGCN的整体框架。

input是交互矩阵和知识图谱,输出是user和item连边的概率。line1开始是KGCN。
我们先不管里面具体的是什么东西,从line2开始,他的意思是对于每一个user和item。我先计算item(v)在知识图谱中的表示,经过h层KGCN之后,最终得到v的表征(line5到lin9),得到表征之后,构造一个函数f()去计算 y ^ u , v {\widehat y}_{u,v} y u,v这最后的输出。所以,KGCN是在知识图谱上对v进行表征学习,perdition head 是其他网络,比如全连接。line4是初始化,line3是对邻居进行采样,这个在单层KGCN再讨论。
整体框架是这个,最核心的是line 3 到9,讲的是KGCN做了什么,line13之后是讲如何对邻域的采样,就是随机采样,不看也没关系。下面讲单层KGCN
单层KGCN
KGCN在我看来其实是GAT的一个翻版。GAT的思想是对一阶邻居节点有区分的聚合。大致算法是先计算一阶邻居对于自身的重要性(系数),再根据重要性区别地聚合邻居信息,KGCN也很类似,首先也是计算重要性。
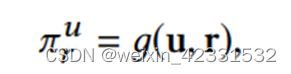
其中 g()是函数,可以简单理解尾u和r的点积。u是user,r是relation. 这个式子可以理解为:user对于哪一类relation更看中。比如有的人喜欢追某个明星的电影看,有的人喜欢追某种类型的电影看。那么不同的user对于relation的偏好是不同的 π r u \pi_r^u πru描绘的就是这个属性。
有了这个偏好之后,单层的KGCN的公式可以表示为:


其中, π r v , e u \pi_{r_{v,e}}^u πrv,eu 表示 实体v 在和它的一阶邻居中的点e,在关系r的情况下的重要性。有点饶人。在知识图谱中,一个实体item是和其他实体entity相连的,他们的relation也不一样。我们已经计算了user对于relation的偏好( π r u \pi_r^u πru),假如v有3个邻居,e1 e2 e3,其中v和e1 e2的关系是r1, 和e3 的关系是r2. 用户u对于r1的喜好假设是0.7,对于r2的喜好是0.2. 那么e1 e2前面 的 π r v , e u \pi_{r_{v,e}}^u πrv,eu就都是0.7,e3的是0.1,把这些系数进行归一化处理,处理好的系数再作为最后从邻居那聚合的系数。这个过程和GAT很像。
这是公式作法。但是在实际中,会遇到一个问题。实体连接的点太多,计算量会很大,为了减少计算复杂度,每个实体固定随机采样,也就是说邻居固定k个,k是采样数。所以在算法流程中line3是采样的过程。一般就随机采样了,比较方便。
在从邻居那聚合函数之后,还有aggravate操作,这是图神经消息传递框架下的正常操作。第一步先从邻居那聚合信息,第二步再和自己的信息进行聚合。
作者做了三种aggravate操作



sum concat 和直接对邻居信息进行变换。
作者后面比较了三种方法的好坏。
实验
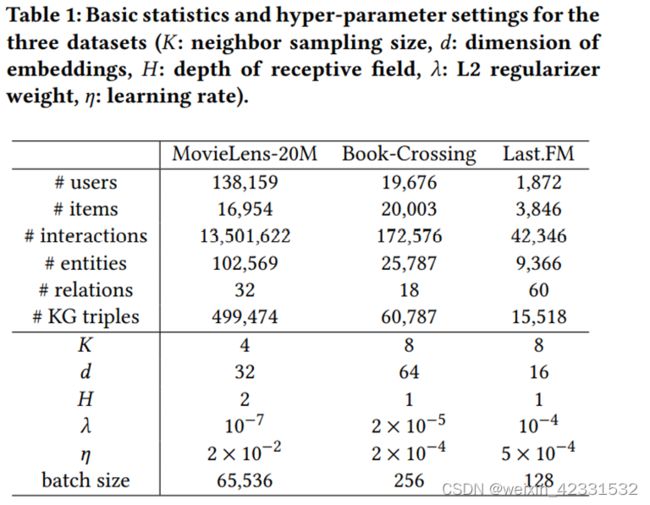
首先是数据集,作者在电影,书籍,音乐三个数据集上做实验,也构建了图谱。我们可以看到,音乐和书籍两个图谱中的关系相对洗漱一些。
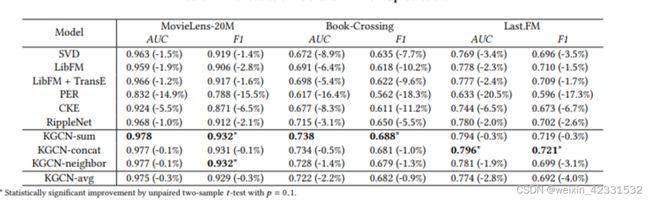
实验的结果。在音乐和书籍中,提升相对来说比电影的要大一些,说明KGCN对于冷启动和稀疏性问题有更好的效果。同时,三种聚合方式的好坏比较,sum的效果最好
消融

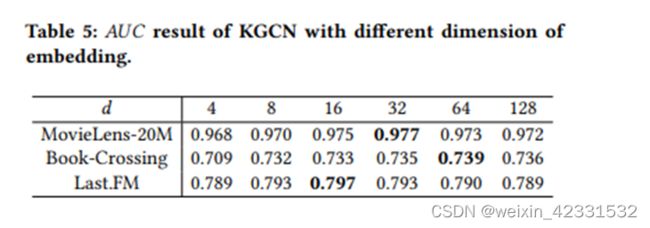
作者对邻居采样,GCN的深度,嵌入维度这三类进行了消融实验。
table3可以看到,太多的邻居反而会引入噪声,降低效果
table4中,GCN的层数不易过多,多了效果反而不好,可能是因为oversmooth问题 。
table5 表明 嵌入的维度过高会导致维度灾难,也不是说越高越好。
看到这里会有问题。知识图谱中的实体如何嵌入成d维度的特征向量? 这涉及知识图谱实体嵌入问题,有transE transR这些技术,是另外一个话题,感兴趣的读者可以自己去搜。