课程笔记：优化器

优化器：
管理并更新梯度的参数
可学习参数是指：权重或偏置
更新策略：梯度下降

基本属性：
defaults: 存储学习率，momentum，weight_decay
state：例如再采用momentum时，会用到前几次更新时使用的梯度，就将其存储在state中，在这次更新中使用
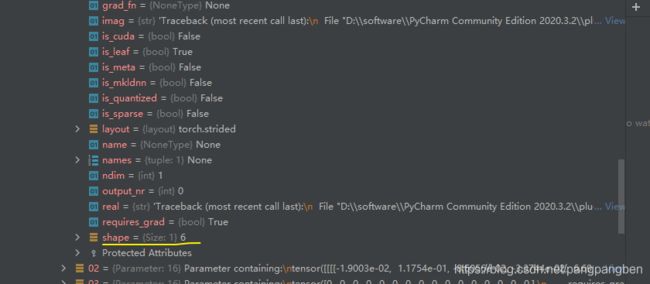
param_groups：管理一系列参数，是list，其中的每一个元素是字典，而字典中的key是最关键的
_step_count：例如在100次的时候下降学习率，在200次的时候再下降学习率

在backward之前，进行梯度清零（zero_grad()）
在完成反向传播后，就要用step()完成更新参数，采用梯度下降的策略，有SGD、adams等
state_dict()与load_state_dict()：用于模型断点的恢复训练

optimizer就有3个属性：default, param_groups, state

param_groups是一个list，每个元素是一个字典，其中params是管理真正的参数的（真正的的可学习参数）

param中：00层表示第一层卷积层的参数，01层表示第一层的偏置；02层表示第二层的参数，03层表示第二层的参数

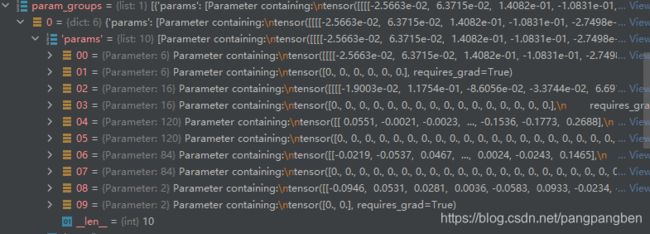
00层中：[6, 3, 5, 5]:其中6表示输出通道数，3表示输入通道数，55表示卷积核的长与宽

01层中：6表示6个偏置

optimizer.step() 的实例：
执行的w=w-lrweight.grad

# weight的梯度需要打开，这里设weight的梯度的元素全为1
weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2)) 
optimizer = optim.SGD([weight], lr=0.1)

print("weight before step:{}".format(weight.data))
optimizer.step()        
print("weight after step:{}".format(weight.data))

输出的结果：
weight before step:tensor([[0.6614, 0.2669],
[0.0617, 0.6213]])
weight after step:tensor([[ 0.5614, 0.1669],
[-0.0383, 0.5213]])

optimizer.zero_grad清空参数的梯度
在优化器当中所管理的参数地址和真实的参数地址一样，所以在优化器中其实保存的是参数的地址，根据地址去找参数，而并非把参数复制过来，节省内存消耗

weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))
optimizer = optim.SGD([weight], lr=0.1)

print("weight in optimizer:{}\nweight in weight:{}\n".format(id(optimizer.param_groups[0]['params'][0]), id(weight)))
print("weight.grad is {}\n".format(weight.grad))
optimizer.zero_grad()
print("after optimizer.zero_grad(), weight.grad is\n{}".format(weight.grad))

结果：
weight in optimizer:1725662867104
weight in weight:1725662867104
weight.grad is tensor([[1., 1.],
[1., 1.]])
after optimizer.zero_grad(), weight.grad is
tensor([[0., 0.],
[0., 0.]])

**optimizer.add_param_group（）**的运用：
在当前已经管理了一组参数，想增加一组参数：首先构建参数，再构建字典

weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))
optimizer = optim.SGD([weight], lr=0.1)

print("optimizer.param_groups is\n{}".format(optimizer.param_groups))
w2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": w2, 'lr': 0.0001})
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

结果：
optimizer.param_groups is
[{‘params’: [tensor([[0.6614, 0.2669],
[0.0617, 0.6213]], requires_grad=True)], ‘lr’: 0.1, ‘momentum’: 0, ‘dampening’: 0, ‘weight_decay’: 0, ‘nesterov’: False}]
optimizer.param_groups is
[{‘params’: [tensor([[0.6614, 0.2669],
[0.0617, 0.6213]], requires_grad=True)], ‘lr’: 0.1, ‘momentum’: 0, ‘dampening’: 0, ‘weight_decay’: 0, ‘nesterov’: False}, {‘params’: [tensor([[-0.4519, -0.1661, -1.5228],
[ 0.3817, -1.0276, -0.5631],
[-0.8923, -0.0583, -0.1955]], requires_grad=True)], ‘lr’: 0.0001, ‘momentum’: 0, ‘dampening’: 0, ‘weight_decay’: 0, ‘nesterov’: False}]

state_dict 通常用于断点的续训练

weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
# 获取state_dict
opt_state_dict = optimizer.state_dict()

print("state_dict before step:\n", opt_state_dict)
# 执行10步的更新，momentum会存储之前的梯度状态信息，先进行一系列更新才有缓存参数
for i in range(10):
	optimizer.step()
print("state_dict after step:\n", optimizer.state_dict())
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

结果：
state_dict before step:
{‘state’: {}, ‘param_groups’: [{‘lr’: 0.1, ‘momentum’: 0.9, ‘dampening’: 0, ‘weight_decay’: 0, ‘nesterov’: False, ‘params’: [0]}]}
state_dict after step:
{‘state’: {0: {‘momentum_buffer’: tensor([[6.5132, 6.5132],
[6.5132, 6.5132]])}}, ‘param_groups’: [{‘lr’: 0.1, ‘momentum’: 0.9, ‘dampening’: 0, ‘weight_decay’: 0, ‘nesterov’: False, ‘params’: [0]}]}

momentum_buffer是指动量中会使用的缓存信息；参数params的地址为0，在state中是通过地址去匹配参数的buffer

load state_dict
加载优化器的state

state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))
optimizer.load_state_dict(state_dict)

学习率

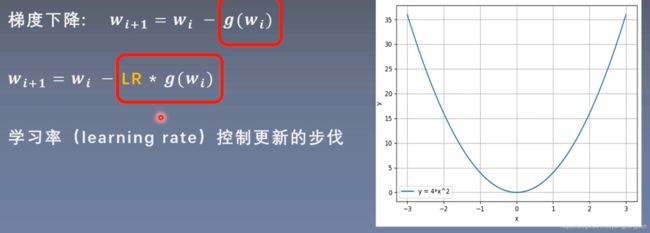
momentum：保持更新的惯性，加快更新的步伐
考虑以前的信息

指数加权平均：
权重呈指数下降
距离当前时刻越远，它对当前时刻的平均值的影响越小；距离当前时刻越近，它的权重越大
Beta: 记忆周期的概念；Beta越小，记忆周期越短。故Beta这个参数是来控制记忆周期。通常Beta=0.9

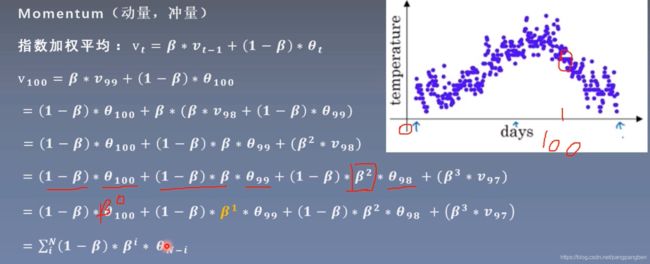
权重呈指数下降

Beta对应到梯度下降中就是momentum这个系数