轨迹优化 | Minimum-jerk

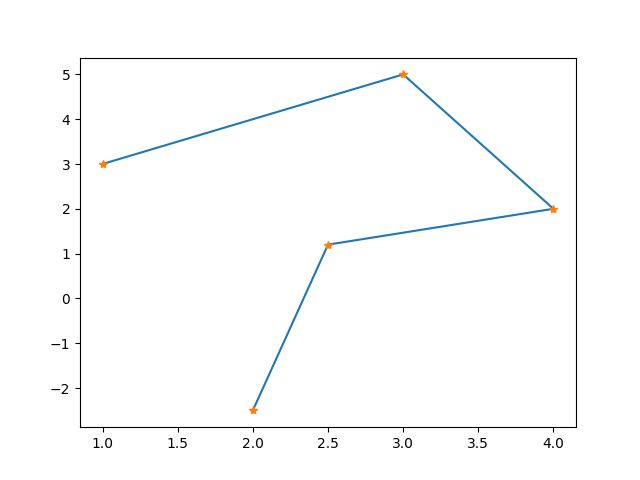
使用路径规划可以得到一系列的路径点，如下图所示有5个路径点，这条路径是很曲折的，这不利于机器人的移动，试想一个机器人直接沿着这条路径进行移动，当到达一个路径点后速度减到零，原地旋转，指向下一个路径点，再继续移动，这不仅智障，而且浪费能量。于是我们就想，能不能规划出一条轨迹，使机器人能够在每一个路径点处能够平滑过渡，从而表现得机灵一点。这就是轨迹规划问题。

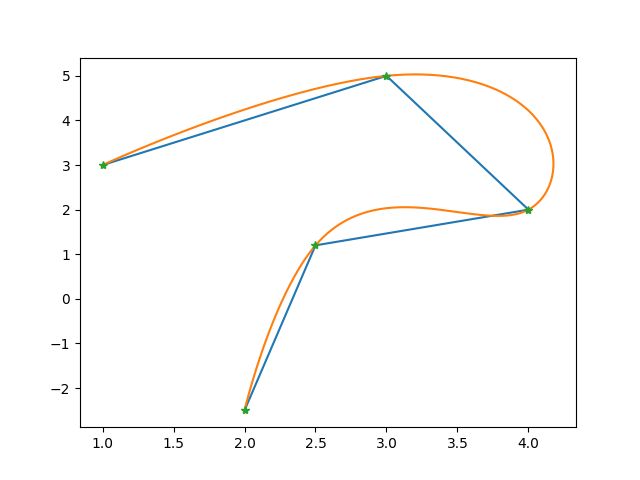
路径规划得到的路径点	轨迹优化得到的轨迹(橙色)

二次规划(Quadratic Programming, QP)

由于轨迹规划问题可以归结为一个二次规划问题，所以这里先对二次规划进行一个简单的介绍

二次型

含有$n$个变量$x=x_1,x_2,\cdots ,x_{n-1},x_n$的二次齐次函数：
$$\begin{array}{rl}f(x_1,x_2,\cdots ,x_n)& =a_{11}{x}_1^2+a_{22}{x}_2^2+\cdots +a_{nn}{x}_n^2\\ & +2a_{12}{x}_1{x}_2+2a_{13}{x}_1{x}_3+\cdots +2a_{n-1,n}{x}_{n-1}{x}_n\end{array}$$
称为二次型。取$a_{ij}=a_{ji}$，则有$2a_{ij}{x}_i{x}_j=a_{ij}{x}_i{x}_j+a_{ji}{x}_j{x}_i$，上式可表示为：
$$f=\sum _{i,j=1}^n{a}_{ij}{x}_i{x}_j$$
矩阵表示为：
$$f=x^{T}Ax$$

二次规划问题

当目标函数$f$为二次型，且约束为线性约束时，该优化问题就是二次规划问题，一般形式表述如下：
$$\begin{array}{rl}\underset{x}{\min }f(x)& =\frac{1}{2}{x}^{T}Qx+q^{T}x\\ s.t.Ax& =b\\ Gx& \le h\end{array}$$
二次规划是一类凸优化问题，目前有很多商业或者开源的求解器来求解这类问题，不再赘述

轨迹表示形式

使用路径规划可以得到一系列的路径点，这些路径点是不带时间信息的，而轨迹则是时间$t$的函数，一般用$n$阶多项式表示，即：
$$\begin{array}{rl}f(t)& =p_0+p_{1}t+p_2{t}^2+\cdots +p_n{t}^n\\ & =\sum _{i=0}^n{p}_i{t}^i\end{array}$$

其中$p_0,p_1,\cdots ,p_n$是轨迹参数，也是我们的优化参数。将$f(t)$写成向量相乘形式，得到：
$$f(t)=\left[\begin{array}{cccc}1& t& \cdots & t^n\end{array}\right]\left[\begin{array}{c}{p}_0\\ p_1\\ ⋮\\ p_n\end{array}\right]$$
对轨迹函数求导，还能写出速度、加速度、jerk等参数随时间变化的函数：

$$\begin{array}{rl}vel(t)& =f^{(1)}(t)=\left[\begin{array}{cccccc}0& 1& 2t& 3t^2& \cdots & \frac{n!}{(n-1)!}{t}^{n-1}\end{array}\right]\cdot p\\ acc(t)& =f^{(2)}(t)=\left[\begin{array}{cccccc}0& 0& 2& 6t& \cdots & \frac{n!}{(n-2)!}{t}^{n-2}\end{array}\right]\cdot p\\ jerk(t)& =f^{(3)}(t)=\left[\begin{array}{cccccc}0& 0& 0& 6& \cdots & \frac{n!}{(n-3)!}{t}^{n-3}\end{array}\right]\cdot p\end{array}$$
其中：$p={\left[\begin{array}{cccc}{p}_0& p_1& \cdots & p_n\end{array}\right]}^T$，概括得到轨迹导数的通式，$k$表示$k$阶导数：
$$f^{(k)}(t)=\left[\begin{array}{cc}\stackrel{\text{k}}{\begin{array}{cccc}0& 0& \cdots & 0\end{array}}& \stackrel{\text{n-k+1}}{\begin{array}{ccccc}\frac{(k+0)!}{0!}{t}^0& \frac{(k+1)!}{1!}{t}^1& \frac{(k+2)!}{2!}{t}^2& \cdots & \frac{n!}{(n-k)!}{t}^{n-k}\end{array}}\end{array}\right]\cdot p$$
一段复杂的轨迹常常需要用多个多项式来表示，可以将完整轨迹按照时间划分成多段，如下，将完整轨迹划分为$M$段多项式轨迹：
$$f(t)=\{\begin{array}{l}\begin{array}{cc}{p}_{1,0}+p_{1,1}t+p_{1,2}{t}^2+\cdots +p_{1,n}{t}^n& T_0\le t\le T_1\\ p_{2,0}+p_{2,1}t+p_{2,2}{t}^2+\cdots +p_{2,n}{t}^n& T_1\le t\le T_2\\ ⋮& \\ p_{M,0}+p_{M,1}t+p_{M,2}{t}^2+\cdots +p_{M,n}{t}^n& T_{M-1}\le t<T_M\end{array}\end{array}$$
其中：$p_{i,j}$表示第$i$段轨迹的第$j$个参数，每段轨迹的时长都是预先分配好的，分配方法以后再叙述，本文暂时设置为固定值。

Minimum-jerk

以下将以Minimum-jerk算法为例来介绍轨迹优化算法的设计流程，Minimum-snap等算法的设计流程与之同理。

Minimum-jerk，顾名思义就是求解每段轨迹的系数$p$使得总的jerk最小，同时还要满足约束条件，所以这是一个带约束的最优化问题，通过后面的证明知道，它其实是一个二次规划问题。

多项式阶次选择

jerk是轨迹$f(t)$的3阶导数，所以令$K=3$。Minimum-jerk会直接对首尾的位置、速度和加速度进行约束，这就有6个等式约束了，所以优化参数必须提供6个以上的自由度，而5阶多项式有6个系数，所以符合要求的多项式的最小阶次为 $Order=5$。同理Minimum-snap还会对首尾的jerk进行约束，所以Minimum-snap的多项式最小阶数为 $7$ 。

因此可以选择五阶多项式来表示每一段轨迹，得到：
$$f(t)=\{\begin{array}{l}\begin{array}{cc}{p}_{1,0}+p_{1,1}t+p_{1,2}{t}^2+p_{1,3}{t}^3+p_{1,4}{t}^4+p_{1,5}{t}^5& T_0\le t\le T_1\\ p_{2,0}+p_{2,1}t+p_{2,2}{t}^2+p_{2,3}{t}^3+p_{2,4}{t}^4+p_{2,5}{t}^5& T_1\le t\le T_2\\ ⋮& \\ p_{M,0}+p_{M,1}t+p_{M,2}{t}^2+p_{M,3}{t}^3+p_{M,4}{t}^4+p_{M,5}{t}^5& T_{M-1}\le t<T_M\end{array}\end{array}$$
其中包含$M$段多项式轨迹，每一段多项式轨迹有$Order+1=6$个系数，一共有$M(Order+1)=6M$个系数

构造目标函数

$jerk(t)$可表示为：
$$\begin{array}{rl}jerk(t)=f^{(3)}(t)& =6p_3+24t{p}_4+60t^2{p}_5\\ & =\left[\begin{array}{cccccc}0& 0& 0& 6& 24t& 60t^2\end{array}\right]\cdot p\end{array}$$
要使其最小，也就是使$jerk(t)$在整段时间上的积分最小，在minimum-jerk中选择使$jerk(t)$的2-范数最小即：
$$\underset{p}{\min }{f}^{(3)}(t)=\underset{p}{\min }\sum _{i=1}^M{\int }_{T_{i-1}}^{T_i}(f^{(3)}(t){)}^{2}dt$$
所以目标函数$J(p)$定义如下：
$$J(p)=\sum _{i=1}^M{\int }_{T_{i-1}}^{T_i}(f^{(3)}(t){)}^{2}dt$$

令$a={\left[\begin{array}{cccccc}0& 0& 0& 6& 24t& 60t^2\end{array}\right]}^T$，对$f^{(3)}(t)$求平方，得到：
$$\begin{array}{rl}(f^{(3)}(t){)}^2& =(\left[\begin{array}{cccccc}0& 0& 0& 6& 24t& 60t^2\end{array}\right]\cdot p{)}^T(\left[\begin{array}{cccccc}0& 0& 0& 6& 24t& 60t^2\end{array}\right]\cdot p)\\ & =(a^{T}p{)}^T(a^{T}p)\\ & =p^{T}a{a}^{T}p\end{array}$$
令$A(t)=a{a}^T$，得到：
$$\begin{array}{r}A=a{a}^T=\left[\begin{array}{c}0\\ 0\\ 0\\ 6\\ 24t\\ 60t^2\end{array}\right]\left[\begin{array}{cccccc}0& 0& 0& 6& 24t& 60t^2\end{array}\right]=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 36& 144t& 360t^2\\ 0& 0& 0& 144t& 576t^2& 1440t^3\\ 0& 0& 0& 360t^2& 1440t^3& 3600t^4\end{array}\right]\end{array}$$
所以$(f^{(3)}(t){)}^2$的积分为：
$$\begin{array}{rl}{\int }_{T_{i-1}}^{T_i}(f^{(3)}(t){)}^{2}dt& ={\int }_{T_{i-1}}^{T_i}{p}^{T}A(t)pdt\\ & =p^T\cdot {\int }_{T_{i-1}}^{T_i}A(t)dt\cdot p\end{array}$$
令$A(t)$的积分为矩阵$Q$，则：
$$Q={\int }_{T_{i-1}}^{T_i}A(t)dt={\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 36t& 72t^2& 120t^3\\ 0& 0& 0& 72t^2& 192t^3& 360t^4\\ 0& 0& 0& 120t^3& 360t^4& 720t^5\end{array}\right]}_{T_{i-1}}^{T_i}$$
最终的目标函数可表述为：
$$\begin{array}{rl}J(p)& =\sum _{i=1}^M{\int }_{T_{i-1}}^{T_i}(f^{(3)}(t){)}^2\\ & =\sum _{i=1}^M{p}_i^T{Q}_i{p}_i\\ & =\left[\begin{array}{cccc}{p}_1^T& p_2^T& \cdots & p_M^T\end{array}\right]\left[\begin{array}{cccc}{Q}_1& & & \\ & Q_2& & \\ & & \ddots & \\ & & & Q_M\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_M\end{array}\right]\\ & =p^{T}Qp\end{array}$$
其中：

• $p={\left[\begin{array}{ccccc}{p}_1^T& p_2^T& \cdots & & p_M^T\end{array}\right]}^T={\left[\begin{array}{cccccccc}{p}_{1,0}& p_{1,1}& \cdots & p_{1,K}& p_{2,0}& \cdots & & p_{M,K}\end{array}\right]}^T$是优化变量，它是每一段多项式轨迹系数的列组合，其维数为$M(Order+1)\times 1$。
• Q是一个维数为$M(Order+1)\times M(Order+1)$的实对称矩阵

显然，$J(p)$是一个二次型，所以基于Minimum-jerk的轨迹优化问题可以转换为一个二次规划问题。

以上定义了Minimum-jerk中的目标函数，接下来添加约束。如果不考虑障碍物，主要有两类约束，一类是导数约束(Derivative Constraint)，它约束了轨迹的初始状态和终止状态，以及每一段轨迹的开始/结束位置，也就是用路径规划得到的路径点对轨迹进行约束；另一类约束是连续性约束(Continuity Constraint)，它可以使相邻轨迹平滑过渡。

导数约束

包含以下约束：

• 初始状态和终止状态约束，如位置、速度、加速度等状态，即：$\{\begin{array}{l}{f}^{(k)}(T_0)=x_0^{(k)}\\ f^{(k)}(T_M)=x_M^{(k)}\end{array},k=0,1,\cdots ,K-1$。
• 每一段轨迹的初始位置由路径点给出，也即：$f_i(T_{i-1})=x_{i-1}$，$i$表示第$i$段轨迹，取值为$i=2,3,\cdots ,M$。

其中$x_0,x_1,\cdots ,x_M$表示路径规划得到的路径点。

对于有$M+1$个路径点的轨迹，一共有$(2K+M-1)$个导数约束

连续性约束

在两段轨迹的连接点处，我们希望这个点处的轨迹是平滑的，可以通过施加连续性约束来实现这个要求，也就是使相邻两段轨迹在连接点处的$0,1,\cdots ,K-1$阶导数分别相等，即：
$$\begin{array}{c}{f}_i(T_i)=f_{i+1}(T_i)\\ f_i^{(1)}(T_i)=f_{i+1}^{(1)}(T_i)\\ ⋮\\ f_i^{(k)}(T_i)=f_{i+1}^{(k)}(T_i)\end{array}$$
其中$i$表示第$i$段轨迹，取值为$i=1,2,\cdots ,M-1$，对于有$M+1$个路径点的轨迹，一共有$M$段多项式轨迹，其中的连续性约束一共有$K(M-1)$个。

对于Minimum-jerk，要求每一段轨迹连接处的位置、速度、加速度一致，也就是：
$$\begin{array}{c}{f}_i(T_i)=f_{i+1}(T_i)\\ f_i^{(1)}(T_i)=f_{i+1}^{(1)}(T_i)\\ f_i^{(2)}(T_i)=f_{i+1}^{(2)}(T_i)\end{array}$$

编程实现

使用Python实现一维的Minimum-jerk算法，其中求解二次规划问题需要用到cvxopt库，安装方法：

pip install cvxopt

完整程序如下：

# -*- coding: utf-8 -*-
"""
Created on Fri Dec 10 2021
一维轨迹优化
@author: ghowoght
"""
#%% 生成路径点
import numpy as np
import matplotlib.pyplot as plt

path = [[1, 3], [3, 5], [4, 2], [2.5, 1.2], [2, -2.5]]
path = np.array(path)
# plt.plot(path[:, 0], path[:, 1])
# plt.plot(path[:, 0], path[:, 1], "*")
# plt.show()

#%% 一维轨迹优化
x = path[:, 0]
# 分配时间
deltaT = 2 # 每一段2秒
T = np.linspace(0, deltaT * (len(x) - 1), len(x))

########### 目标函数 ###########
######## 1/2xTQx + qTx ########
K = 3                   # jerk为3阶导数，取K=3
n_order = 2 * K - 1     # 多项式阶数
M = len(x) - 1          # 轨迹的段数
N = M * (n_order + 1)   # 矩阵Q的维数

def getQk(T_down, T_up):
    Q = np.zeros((6, 6))
    Q[3][4] =  72 * (T_up**2 - T_down**2)
    Q[3][5] = 120 * (T_up**3 - T_down**3)
    Q[4][5] = 360 * (T_up**4 - T_down**4)
    Q = Q + Q.T # Q为对称矩阵
    Q[3][3] =  36 * (T_up**1 - T_down**1)
    Q[4][4] = 192 * (T_up**3 - T_down**3)
    Q[5][5] = 720 * (T_up**5 - T_down**5)
    return Q
    
Q = np.zeros((N, N))
for k in range(1, M + 1):
    Qk = getQk(T[k - 1], T[k])
    Q[(6 * (k - 1)) : (6 * k), (6 * (k - 1)) : (6 * k)] = Qk

Q = Q * 2 # 因为标准目标函数为： 1/2xTQx + qTx，所以要乘2

########### 约束 ###########
# 1.导数约束 Derivative Constraint
A0 = np.zeros((2 * K + M - 1, N)) 
b0 = np.zeros(len(A0))

# 添加首末状态约束(包括位置、速度、加速度)
for k in range(K): 
    for i in range(k, 6):
        c = 1
        for j in range(k):
            c *= (i - j)
        A0[0 + k * 2][i]                = c * T[0]**(i - k)
        A0[1 + k * 2][(M - 1) * 6 + i]  = c * T[M]**(i - k)
b0[0] = x[0]
b0[1] = x[M]
# 添加每段轨迹的初始位置约束
for m in range(1, M):
    for i in range(6):
        A0[6 + m - 1][m * 6 + i] = T[m]**i
    b0[6 + m - 1] = x[m]

# 2.连续性约束 Continuity Constraint
A1 = np.zeros(((M - 1) * 3, N))
b1 = np.zeros(len(A1))
for m in range(M - 1):
    for k in range(3): # 最多两阶导数相等    
        for i in range(k, 6):
            c = 1
            for j in range(k):
                c *= (i - j)
            index = m * 3 + k
            A1[index][m * 6 + i] = c * T[m + 1]**(i - k)
            A1[index][(m + 1)* 6 + i] = -c * T[m + 1]**(i - k)
A = np.vstack((A0, A1))
b = np.hstack((b0, b1))
#%% 解二次规划问题
from cvxopt import matrix, solvers
# 目标函数
Q = matrix(Q)
q = matrix(np.zeros(N))
# 等式约束: Ax = b
A = matrix(A)
b = matrix(b)
result = solvers.qp(Q, q, A=A, b=b)
p_coff = np.asarray(result['x']).flatten()

#%% 可视化x轴优化结果
Pos = []
Vel = []
Acc = []
for k in range(M):
    t = np.linspace(T[k], T[k + 1], 100)
    t_pos = np.vstack((t**0, t**1, t**2, t**3, t**4, t**5))
    t_vel = np.vstack((t*0, t**0, 2 * t**1, 3 * t**2, 4 * t**3, 5 * t**4))
    t_acc = np.vstack((t*0, t*0, 2 * t**0, 3 * 2 * t**1, 4 * 3 * t**2, 5 * 4 * t**3))
    coef = p_coff[k * 6 : (k + 1) * 6]
    coef = np.reshape(coef, (1, 6))
    pos = coef.dot(t_pos)
    vel = coef.dot(t_vel)
    acc = coef.dot(t_acc)
    Pos.append([t, pos[0]])
    Vel.append([t, vel[0]])
    Acc.append([t, acc[0]])
Pos = np.array(Pos)
Vel = np.array(Vel)
Acc = np.array(Acc)
plt.subplot(3, 1, 1)
plt.plot(Pos[:, 0, :].T, Pos[:, 1, :].T)
# plt.title("position")
plt.xlabel("time(s)")
plt.ylabel("position(m)")
plt.subplot(3, 1, 2)
plt.plot(Vel[:, 0, :].T, Vel[:, 1, :].T)
# plt.title("velocity")
plt.xlabel("time(s)")
plt.ylabel("velocity(m/s)")
plt.subplot(3, 1, 3)
plt.plot(Acc[:, 0, :].T, Acc[:, 1, :].T)
# plt.title("accel")
plt.xlabel("time(s)")
plt.ylabel("accel(m/s^2)")
plt.show()

x轴上的规划结果如下，可以看到生成轨迹的位置、速度和加速度曲线都是连续的。

分别求X轴和Y轴方向的轨迹，合并后的结果如下图，程序见这里

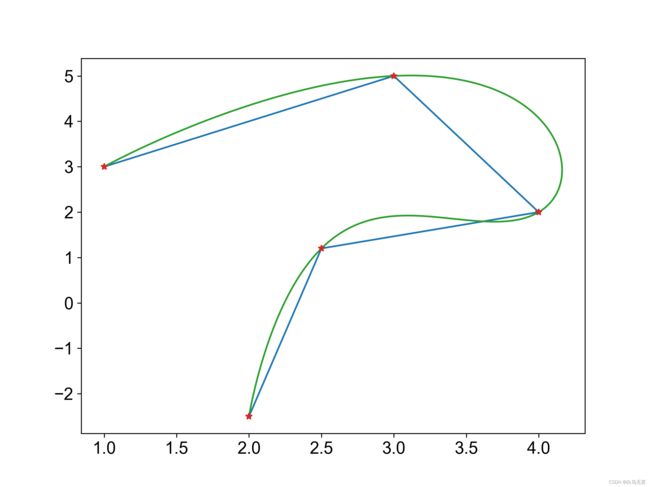
参考

Minimum Snap轨迹规划详解

浅谈「正定矩阵」和「半正定矩阵」