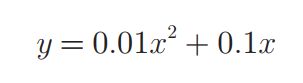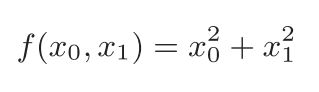机器学习 微分梯度python实现

1. 用数值微分对简单函数进行求导
   

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt

#微分方程
def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

#函数的表达形式
def function_1(x):
    return 0.01*x**2 + 0.1*x 

#切线 x 为传入点5的斜率
def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)#0.1999999999990898 接近于2
    y = f(x) - d*x#计算x=5 y的值
    return lambda t: d*t + y#函数表达式 d*t + y
     
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function_1, 5)
y2 = tf(x)#与曲线用同样的点

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

曲面函数求解

2) 偏导数求导

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

fig = plt.figure()
ax1 = plt.axes(projection="3d")

x1 = np.arange(-10,10,0.1)
x2 = np.arange(-10,10,0.1)
#网格数据采集函数,否则是一条曲线不是曲面
X,Y=np.meshgrid(x1,x2)
Z = X**2 +Y**2
ax1.plot_surface(X,Y,Z,cmap="binary")#,alpha=0.5
#ax1.plot3D(X,Y,Z)  去掉meshgrid使用就是现实曲线
plt.show()

def numerical_diff(f, x):
    h = 1e-4  # 0.0001
    return (f(x + h) - f(x - h)) / (2 * h)
def function_tmp1(x0):
    return x0*x0 + 4.0** 2.0
#x1处的偏导
def function_tmp2(x1):
    return 3.0*2.0 + x1*x1

var = numerical_diff(function_tmp1,3.0)
print(var)#6.00000000000378
var = numerical_diff(function_tmp2,4.0)
print(var)#7.999999999999119
#和解析解的值基本一致

3）梯度求导

# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

#梯度算法核心 
def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        
    return grad


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad


def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)


def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y
     
if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()
    
        #va = numerical_gradient(function_2, np.array([3.0, 4.0]))
    #print(va)#[6. 8.] 越远梯度越大
    #va = numerical_gradient(function_2, np.array([0.0, 2.0]))
    #print(va)# [0. 4.]越近梯度越小
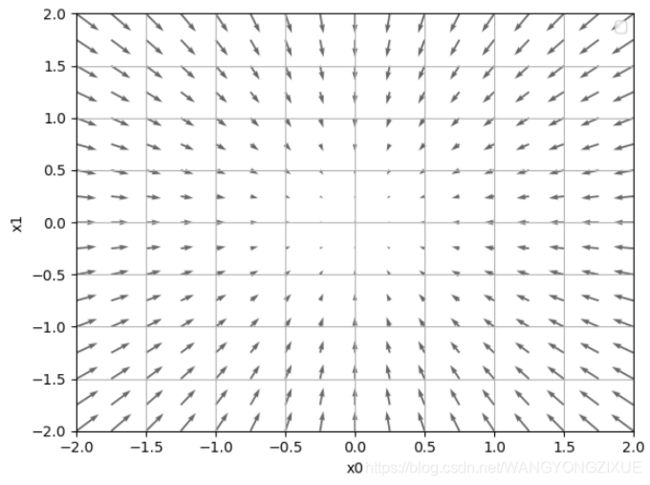
    grad = numerical_gradient(function_2, np.array([X, Y]) )
    
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

程序运行结果

def function_2(x):
    return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])#初始值选择

#寻找最小值
var = gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
print(var)#逐渐趋向于[0,0]

#输出结果，循环100 次逐渐趋向于[0,0]
       [-3.00000000e+00,  4.00000000e+00],
       [-2.40000000e+00,  3.20000000e+00],
       [-1.92000000e+00,  2.56000000e+00],
       ...
       [-1.19357577e-09,  1.59143436e-09],
       [-9.54860614e-10,  1.27314749e-09],
       [-7.63888491e-10,  1.01851799e-09]

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
from gradient_2d import numerical_gradient


def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad# x值逐渐变化 趋向于[0,0]

    return x, np.array(x_history)


def function_2(x):
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])    

lr = 0.1
step_num = 200
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
print(x)#-1.25592487e-19  1.65436123e-19
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')

plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()

值逐渐向[0,0]靠近