损失函数
作用
在有监督的学习中,需要衡量神经网络输出和所预期的输出之间的差异大小。这种误差函数需要能够反映出当前网络输出和实际结果之间一种量化之后的不一致程度,也就是说函数值越大,反映出模型预测的结果越不准确。
还是拿练枪的Bob做例子,Bob预期的目标是全部命中靶子的中心,但他现在的命中情况是这个样子的:
![]()
最外圈是1分,之后越向靶子中心分数是2,3,4分,正中靶心可以得5分。
那Bob每次射击结果和目标之间的差距是多少呢?在这个例子里面,用得分来衡量的话,就是说Bob得到的反馈结果从差4分,到差3分,到差2分,到差1分,到差0分,这就是用一种量化的结果来表示Bob的射击结果和目标之间差距的方式。也就是误差函数的作用。因为是一次只有一个样本,所以这里采用的是误差函数的称呼。如果一次有多个样本,那么就要称呼这样子衡量不一致程度的函数就要叫做损失函数了。
![]()
以做线性回归的实际值和预测值为例,若自变量x是[-2, -1, 0, 1, 2]这样5个值,对应的期望值y是[-3, 0, 0, 3, 4]这样的值,目前预测使用的参数是(w, b) = (2, 1), 那么预测得到的值y_ = [-3, -1, 1, 3, 5], 采用均方误差计算这个预测和实际的损失就是∑4i=0(y[i]−y_[i])2∑i=04(y[i]−y_[i])2, 也就是3。那么如果采用的参量是(0, 0),预测出来的值是[0, 0, 0, 0, 0],这是一个显然错误的预测结果,此时的损失大小就是34,3<343<34, 那么(2, 1)是一组比(0, 0)要合适的参量。
那么常用的损失函数有哪些呢?
这里先给一些前提,比如神经网络中的一个神经元:
![]()
常用损失函数
- MSE (均方误差函数)
该函数就是最直观的一个损失函数了,计算预测值和真实值之间的欧式距离。预测值和真实值越接近,两者的均方差就越小。
- 想法来源
在给定一些点去拟合直线的时候(比如上面的例子),常采用最小二乘法,使各个训练点到拟合直线的距离尽量小。这样的距离最小在损失函数中的表现就是预测值和真实值的均方差的和。 -
函数形式:
loss=12∑i(y[i]−a[i])2,
其中, aa是网络预测所得到的结果,yy代表期望得到的结果,也就是数据的标签,ii是样本的序号。 -
反向传播:
∂loss∂z=∑i(y[i]−a[i])∗∂a[i]∂z
-
缺点:
和∂a[i]∂z∂a[i]∂z关系密切,可能会产生收敛速度缓慢的现象,以下图为例(激活函数为sigmoid)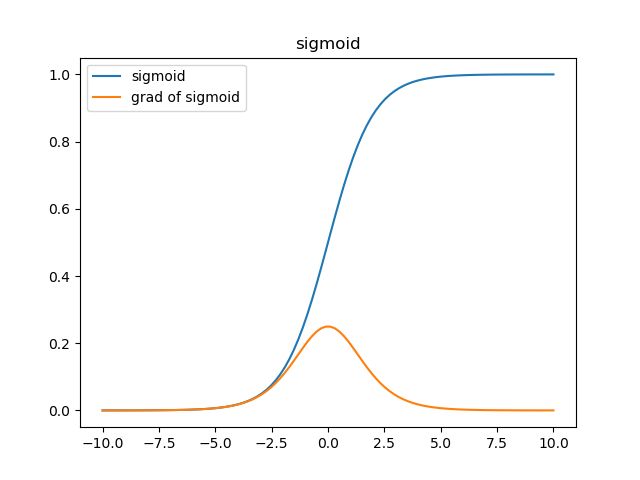
在激活函数的两端,梯度(黄色)都会趋向于0,采取MSE的方法衡量损失,在aa趋向于1而yy是0的情况下,损失loss是1,而梯度会趋近于0,在误差很大时收敛速度也会非常慢。
在这里我们可以参考activation中关于sigmoid函数求导的例子,假定x保持不变,只有一个输入的一个神经元,权重w=ln(9)w=ln(9), 偏置b=0b=0,也就是这样一个神经元:

保持参数统一不变,也就是学习率η=0.2η=0.2,目标输出y=0.5y=0.5, 此处输入x固定不变为x=1x=1,采用MSE作为损失函数计算,一样先做公式推导,
第一步,计算当前误差
loss=12(a−y)2=12(0.9−0.5)2=0.08
第二步,求出当前梯度
grad=(a−y)×∂a∂z∂z∂w=(a−y)×a×(1−a)×x=(0.9−0.5)×0.9×(1−0.9)×1=0.036
第三步,根据梯度更新当前输入值
w=w−η×grad=ln(9)−0.2×0.036=2.161
第四步,计算当前误差是否小于阈值(此处设为0.001)
a=11+e−wx=0.8967
loss=12(a−y)2=0.07868第五步,重复步骤2-4直到误差小于阈值