深度学习第四课——深度卷积网络(week 2)
目录
二、深度卷积网路
2.1 经典网络结构
2.1.1 LeNet - 5
2.1.2 AlexNet
2.1.3 VGG - 16
2.2 残差网络(ResNets - Residual Networks)
2.3 残差网络为什么有用
2.4 网络中的网络及1×1卷积
2.5 Inception网络
2.5.1 介绍
2.5.2 应用
2.6 使用开源的实现方案
2.7 迁移学习
2.8 数据扩充(数据增强)
2.8.1 常见增强方法
2.8.2 色彩转换
2.9 深度学习现状
二、深度卷积网路
2.1 经典网络结构
2.1.1 LeNet - 5
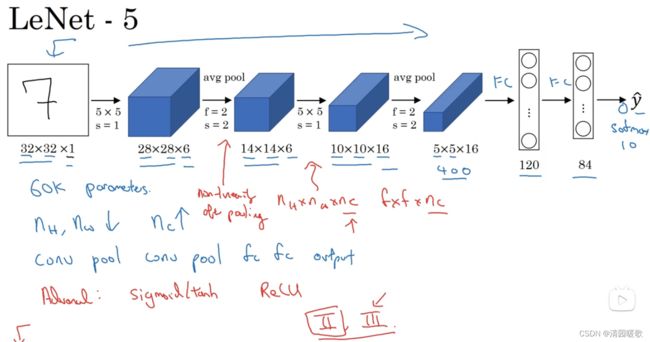
LeNet - 5 可以识别手写数字集,是针对灰度图像训练的
如下例:
先用6个过滤器,f=5,s=1,输出28×28×6,再池化,再用16个过滤器,再次池化,这一层有5×5×16=400个节点,下一层为全连接层,每个节点有120个神经元;但有时还会从这400个节点中抽取一部分节点构建另一个全连接层,利用这最后的84个节点得到最后的输出
可以看出,随着网络深度的加深,图像的高度和深度都在缩小,信道数量在增加
大约有 6w 个参数
2.1.2 AlexNet
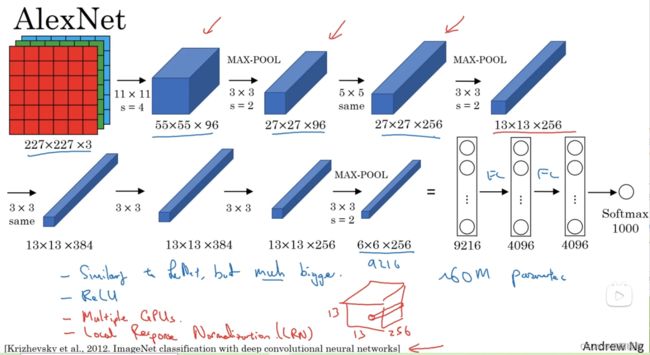
用 227×227×3 作为输入,使用96个过滤器,f=11,s=4,构建池化层,same卷积和256个过滤器后后变成27×27×256,再池化,再做same卷积,384个过滤器;在做一个相同的3×3的卷积,然后再做一次,过滤器256个,最后在进行一次最大池化,缩小为6×6×256=9216个单元,然后是全连接层,使用softmax函数输出,看他是1000个可能的对象中的哪一个
和前面的 LeNet - 5 很类似,只不过大了很多,AlexNet 包含了约 6000w 个参数,当用于训练图像和数据集时,AlexNet能够处理非常相似的基本构造模块,这些模块往往包含大量的隐藏单元或数据。另一个比 LeNet - 5 更出色的原因是,它使用了ReLu激活函数,
局部响应归一化层(LRN):选取一个位置穿过所有信道,进行归一化,动机是对于这张13×13的图像中高度每个位置来说,我们可能并不需要太多的高激活神经元,但后来发现LRN好像并不能起到很大的作用
2.1.3 VGG - 16
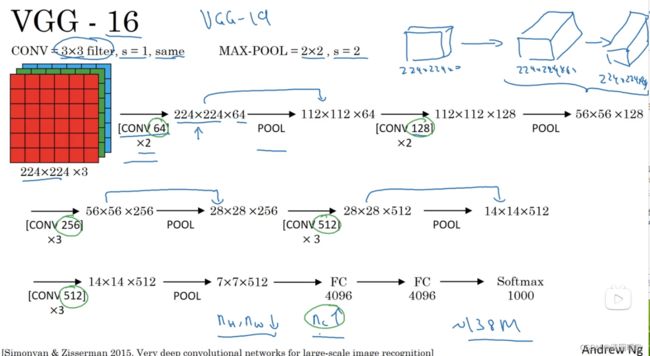
VGG 也叫 VGG - 16,VGG - 16网络没有那么多参数,这是一种只需要专注于构建卷积层的简单网络。
首先用3×3、步幅s=1的过滤器构建same卷积层,再构建最大池化层,f=2,s=2,因此VGG - 16的一大优点就是确实简化的神经网络结构
首先用两个相同的卷积层卷积,在构建池化层,减半后;再连续两个卷积层,再池化,输出56×56×128,在进行3次卷积后池化,在卷积三次,再池化;如此进行几轮后,得到7×7×512,进行全连接,得到4096个单元,然后softmax激活,输出从1000个对象中识别的结果。
VGG - 16中的16是指这个网络包含16个卷积层和全连接层,约有1.38亿个参数;主要缺点是需要训练的特征数量非常巨大。VGG - 16和VGG - 19几乎不分上下,所以很多人还是喜欢VGG - 16
可以看出,图像的缩小比例和信道增加的比例是有规律的
2.2 残差网络(ResNets - Residual Networks)
非常非常深的网络是很难训练的,因为存在梯度消失和梯度爆炸的问题。这节课,学习远眺连接,他可从某一网络层获得激活,然后迅速反馈给另外一层,甚至是神经网络的更深层,我们可以利用远眺连接构建能够训练深度网络的ResNets,有时深度能超过100层
ResNets 是由残差块构建的,什么是残差块?(ResNets 发明者是 何恺明、张翔宇、任少卿、孙剑)
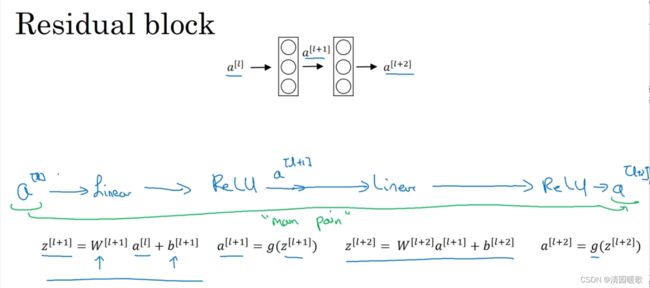
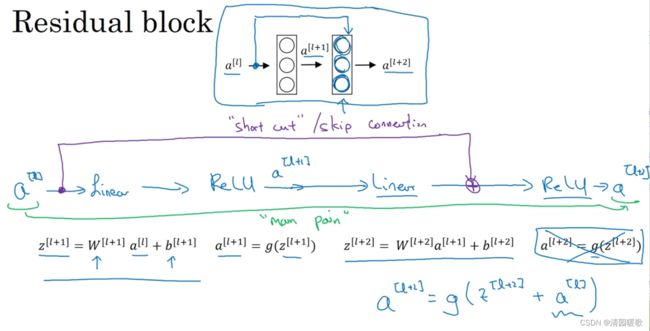
如图,是一个两层的神经网络,再L层激活得到a[l+1]再次激活得到a[l+2]。
计算过程是从 a[l] 开始,首先进行线性激活,算出z[l+1] 然后通过 ReLu,非线性激活得到 a[l+1],a[l+1] = g(z[l+1]),再次进行线性激活,得到z[l+2],再进行ReLu,得到 a[l+2],ReLu指非线性函数
而残差网络中有一点变化,我们将 a[l] 直接向后,拷贝到神经网络的深层,走一个结晶(short cut)再ReLU非线性激活前加上 a[l] 。意味着最后一个等式去掉了,取而代之的是另一个ReLU非线性函数,仍然对z[l+2]进行g函数处理,但这次要加上 a[l],也就是加上了这个 a[l] 产生的一个残差块;a[l] 插入的时机是线性函数之后,非线性激活之前。还有一个术语“远跳连接”
远跳连接(skip connection):就是指a[l] 跳过一层或好几层,从而将信息传递到神经网络的更深层
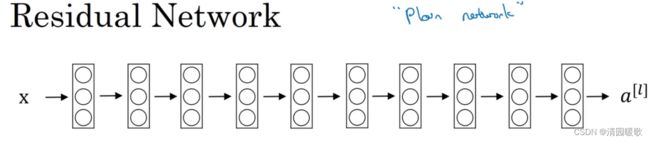
所以ResNets网络就是通过将很多这样的残差块堆积在一起,形成一个深度神经网络,
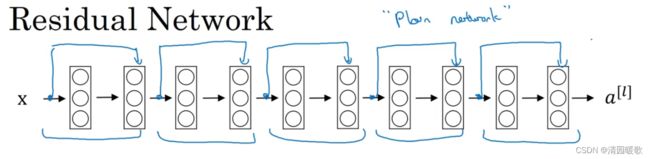
要把下面的普通网络,变成ResNet的方法就是加上所有的远跳连接,或者说捷径
如下图,5个残差块连接在一起,构成一个残差网络,
如果用其他算法,而没有多余的残差、捷径,会发现随着网络深度的加深,训练错误会减少,然后增多;理论上,随着深度的加深,应该越来越好才对,也就是说神经网络深度越深越好,但是如果没有残差网络,对于普通网络而言,深度越深意味着用优化算法越难训练,训练错误会越来越多。而有了ResNet,网络深度越深,效果越好,也许另一个角度来看,越深会显得网络更臃肿,但确实再训练深度网络方面非常有效
2.3 残差网络为什么有用
假设有一个大型神经网络,其输入为X,输出激活值为 a[l],如果想增加这个网路的深度,一次添加两层,输出为 a[l+2],把这添加的两层看作一个ResNet块,即具有近路连接的残差块。
为方便说明,假设整个网络都是用ReLU激活函数,所有激活值都大于等于0,包括输入x的非零异常值,因为relu输出的值要么是0,要么是正数
随着模型的不断学习,如果使用了正则化(一种可以使w值逐渐变小的方法),w值就会越来越小。这可能会使后面的神经元的输出值都非常小(或是0)
这里也假设了b的值也会越来越小 这时候如果没有使用残差快 那么wa+b的值就会成为0
还有最重要的就是,当反向传播计算梯度的时候,由于输入的小,梯度就会消失,这时候相当于后面的神经元什么都没有学习到,因为梯度不再下降了,或者说下降的很小;但是引入残差块,就算w b为0,激活值也不会为0,从而解决了梯度消失和梯度爆炸的问题
结果表明,残差块学习这个恒等式函数残差块并不难,跳远连接使我们很容易得出 a[l+2] = a[l],这意味着即使给神经网络增加了这两层,它的效率也并不逊色于更简单的神经网络,因为学习恒等函数对他来说很简单。尽管它多了两层,也只是把 a[l] 的值赋给 a[l+2]。即 这保证了深度的增加不会给模型带来负面影响,至少不会比简单网络差
所以给大型神经网络增加两层,不论是把残差块添加到神经网络的中间还是末端位置,都不会影响网络的表现,当然我们的目标不仅仅是保持网络效率,还要提升它的效率,想象一下,如果这些隐层单元学到一些有用信息,那么它可能比学习恒等函数表现得更好。
而这些不含有残差块或跳远连接的深度普通网络情况就不一样了,当网络不断加深时,就算是选择用来学习恒等函数的参数都很困难
残差网络起作用的很大原因就是这些残差块学习恒等函数非常容易,能确定网络性能不会受到影响,很多时候甚至可以提高效率,或者说至少不会降低网络效率
其他理解:
W[l+2],b[l+2]就相当于一个开关,而是否把这两个参数置为0就要看反向传播,网络最终能够知道到底要不要skip,只要让这两个为0,就可以达到增加网络深度却不影响网络性能的目的
何凯明说过其实alexnet是解决太深导致梯度消失,因为随着层数的增加计算出的梯度会慢慢变小,可以映射到激活值会慢慢变小,之后他就想加一个远眺链接就可以保证无论中间多少层,最终两端激活值大体上不改变
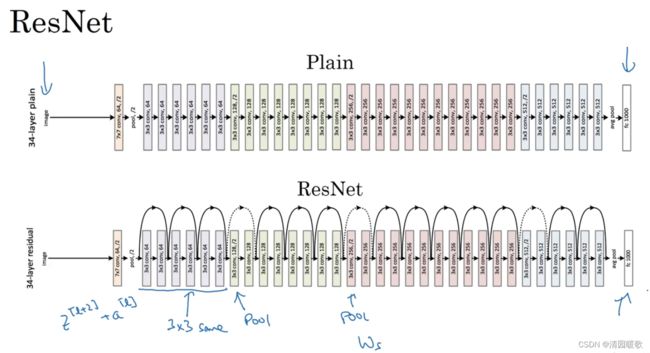
残差网络另一个值得讨论的细节是,假设z[l+2]与a[l]具有相同维度,所以ResNets使用了许多相同卷积,所以这个 a[l]的维度等于这个输出层的维度,因而实现这个跳远连接,因为同一个卷积保留了维度,所以很容易得出这个短连接
如果输入输出是不同的维度,a[l]是128,a[l+2]是256,再增加一个矩阵就在增加一个矩阵 Ws,Ws是一个256×128维度的矩阵,所以Ws a[l]的维度是256。不需要对Ws做任何操作,他是网络通过学习得到的矩阵或参数,他是一个固定矩阵,padding值为0,用0填充a[l],其维度是256
一个图像分类的例子,这是普通网络,输入一张图片,有多个卷积层,最后输出了一个softmax,如何转化成resnet,只需添加跳远连接。无论这些层是什么类型,都需要调整矩阵Ws的维度,普通网络和ResNet网络常用的结构是conv,conv,conv,pppl之类依次重复,最后有一个通过softmax进行预测的全连接层
2.4 网络中的网络及1×1卷积
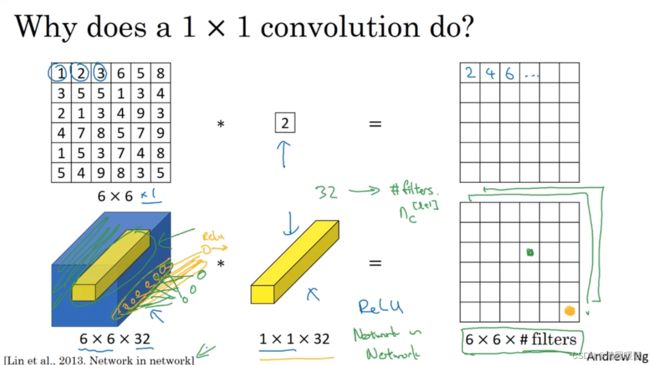
使用1×1卷积,如果是上例 6×6×1 的图片而言,1×1卷积效果不佳,如果是 6×6×32 的图片,那么使用1×1 过滤器进行卷积效果更好。有时也被称为Network in Network
具体来说,1×1卷积所实现的功能是遍历这36个单元格,计算左图中32个数字和过滤器中32个数字的元素智能乘积,然后应用ReLU非线性函数
以其中一个单元格为例,他是这个输入层上的某个切片,这个1×1×32过滤器中的32个数字可以理解为:一个神经元的输入是32个数字,乘以相同高度和宽度上某个切片的32个数字,这32个数字具有不同信道,乘以32个权重,然后应用ReLu非线性函数,输出相应的结果
所以1×1卷积可以从根本上理解为这32个单元都应用了一个全连接神经网络,全连接层的作用是输入32个数字和过滤器数量,标记为nc[l+1],在36个单元上重复此过程
即 把同行同列的32个数看作是神经元输入, 把filter的32个数看成是权重, 结果就会得到一个输出, 经过ReLu函数, 获得一个输出, 对于多个filter, 就有多层的输出
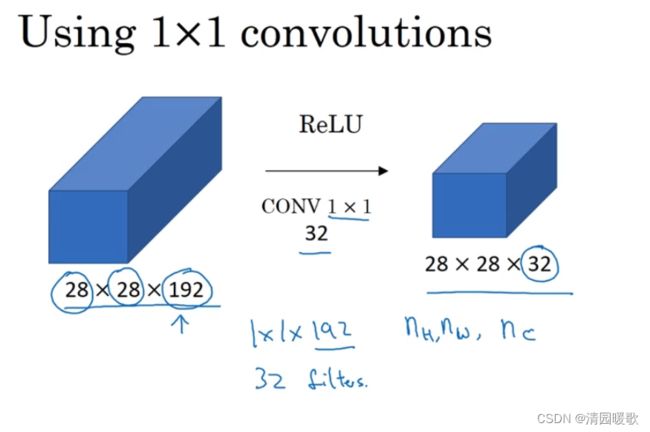
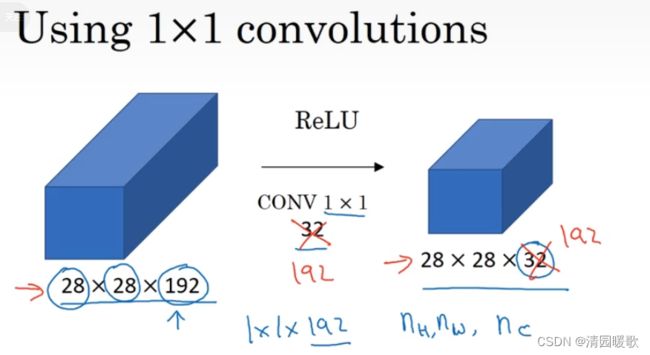
如果要把一个 28×28×192 的图片缩小成 28×28×32 的就可以用32个1×1 的过滤器,严格来讲,每个过滤器的大小都是 1×1×192 维,因为过滤器中信道的数量必须与输入层中信道的数量一致。池化层是压缩了高度nw和宽度nw,这里压缩了nc
1 × 1卷积层就是这样实现了一些重要功能,他给神经网络添加了一个非线性函数,从而减少或保持输入层中信道数量不变,也可以增加信道数量,这对构建 Inception 网络很有帮助
2.5 Inception网络
2.5.1 介绍
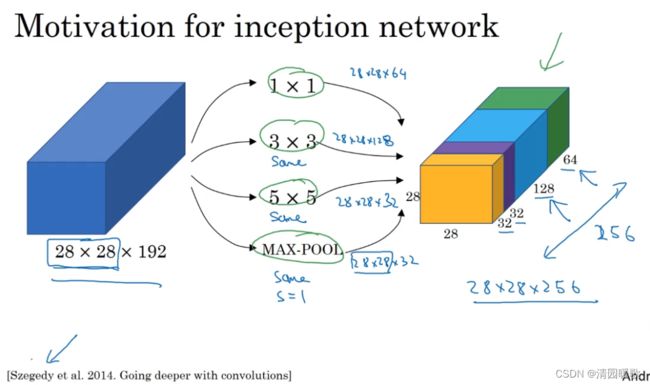
构造卷积层时,你要决定过滤器的大小究竟时1×3,还是3×3,还是5×5,或者要不要添加池化层,而Inception网络的作用就是代替你来做决定,虽然网络架构因此变得更加复杂,但网络表现却非常好
这里池化后维度变了,是又进行了一次 1×1卷积,
基本思想是:Inception网络不需要认为决定使用哪个过滤器, 或是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能的值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合,但有个问题就是计算代成本
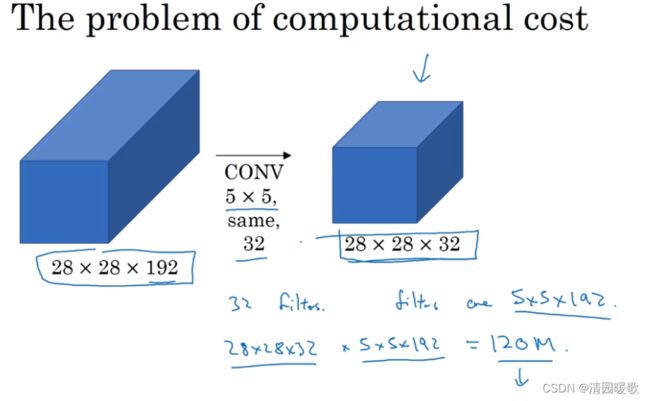
下面计算一个这个5×5 过滤器的成本,
这个计算量的理解:5*5*192是指一个过滤器的在输入上的乘法数量,28*28*32是指,32个过滤器在每个卷积核中的乘积次数,对于输出的 28×28×32 的每个数字都要进行 5×5×192次乘法运算 = 120M 。为了降低计算成本,我们用计算成本除以因子10,缩小为十分之一
另一种方法如下,应用1×1卷积:
要做的就是把左边这个较大的输入层,压缩成中间较小的中间层,只有16个信道,有时这被称为瓶颈层,通常是某个对象最小的部分。中间的成本是 输出 28×28×16每个都做1×1差192次乘法= 240w,而第二个卷积层为 28 ×28×32 × 5×5×16 = 1000w = 10M,总次数是1240w = 12.4M,而所需的加法运算和乘法运算近似相等
当你不想决定是否用池化层,用什么过滤器时,可以用 Inception 模块,应用各种过滤器,只需把输出连起来,而计算成本,可以用1×1卷积构建瓶颈层,只要合理构建瓶颈层就不会影响性能。。。。。
2.5.2 应用
这个模型的目的是让模型自己学习用哪一种conv的方式,就不需要不停调参了,简化运算也少费很多人力
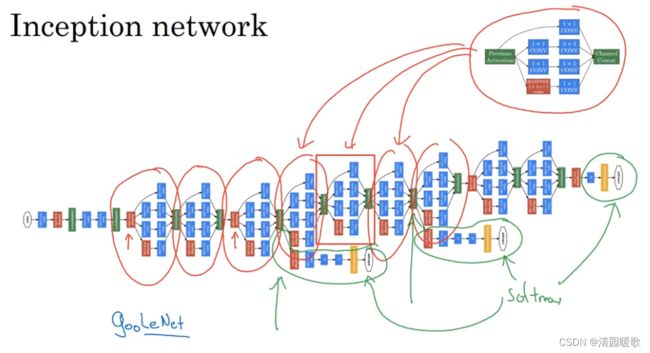
如下图,中间通过一些全连接层,然后softmax来预测输出结果标签,可以看错Inception网络的一个细节,他确保了即使是隐藏单元和中间层,也参与了特征计算,他们也能预测图片的分类,它在Inception网络中起到一种调整的效果,并且能防止网络发生过拟合
Inception 这个命名来自盗梦空间的网络流行梗。。。
2.6 使用开源的实现方案
面向 GitHub编程(狗头)
复制URL
然后git clone ,这是用git下载
还有直接下载
如果在开发一个计算机视觉应用,一个常见工作流程就是先选择一个你喜欢的架构,你学习过的、朋友介绍的、文献看到的,然后寻找一个开源实现,从GitHub下载,以此为基础开始构建,优点是这些网络通常都需要很长时间来训练,而或许有人已经使用多个GPU,通过庞大的数据集预先训练了这些网络,接下来就可以对这些网络迁移学习
2.7 迁移学习
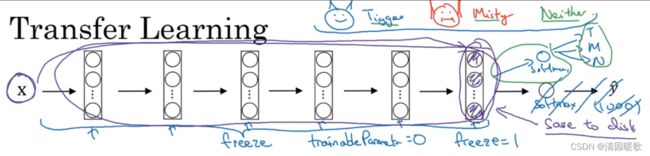
比如做一个猫检测器,你的数据集很少,就可以下载一个网络,去掉他的输出1000个的softmax,加上你自己输出的 tigger,misty,neither 的3个类别
其次一个方法就是把前面的神经网络都当成输入存储起来,只训练softmax这一层
如果你的数据集大了一点,可以只选择冻结前面少部分的层,训练后面的;或者重新构建后面的层和softmax输出。
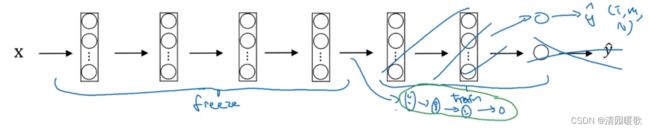 有一个规律,如果你有越多的数据,你需要冻结的层数越少,你能够训练的层数就越多
有一个规律,如果你有越多的数据,你需要冻结的层数越少,你能够训练的层数就越多
而如果有大量的数据,要做的就是 用开源的网络和它的权重,把整个的当作初始化,然后训练整个网络,改变成你自己的softmax输出层
2.8 数据扩充(数据增强)
2.8.1 常见增强方法
(1)垂直镜像对称
(2)随机裁剪
(3)旋转
(4)剪切
(5)扭曲变换
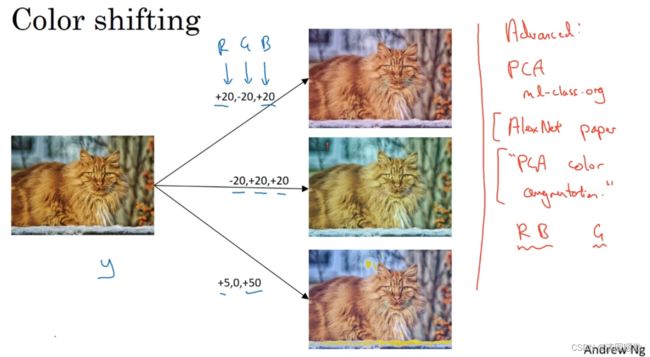
2.8.2 色彩转换
改变r,g,b的值,根据某种分布
PCA颜色增强:比如你的图片总体偏紫色,即红色、蓝色多一点,绿色少一点,则变化时就会红、蓝色增强多一点,绿色少一点
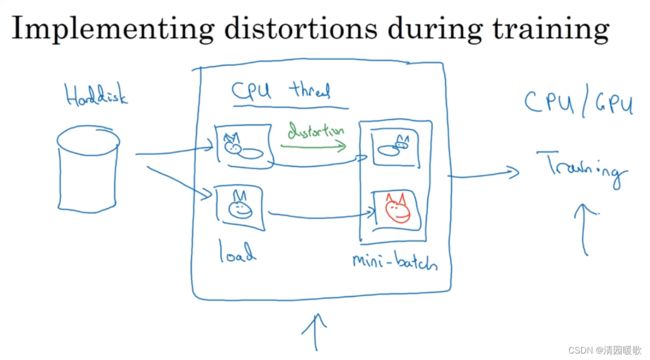
用cpu线程对存储在硬盘中的数据图片进行处理,镜像、或是颜色增强等,cpu线程持续的加载数据,然后实现任意扭曲,从而构成最小批数据或批数据,这些数据持续输出给其他线程或者其他的进程,然后开始训练,这些可以在cpu或很大的神经网络可以在gpu上实现
数据处理和训练可以并行实现
2.9 深度学习现状
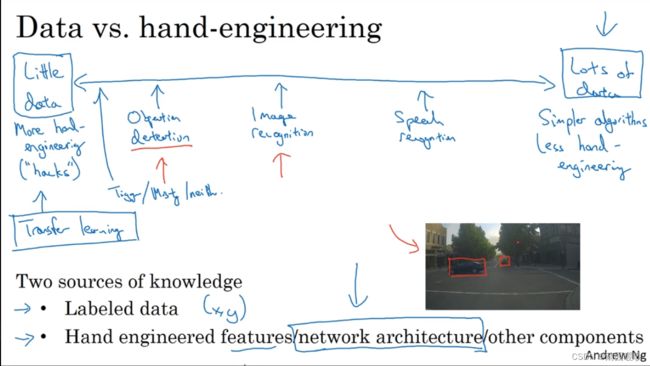
从较少数据应用到大量数据
从左到右:物体检测、图像识别、语音识别,越多的数据可以代表越少的手工工程,去建立学习系统
通常认为我们的学习算法有两种来源:被标记的数据、手工工程