群体智能优化算法介绍
群体智能优化算法介绍
群体智能(Swarm Intelligence)算法的定义:
群体智能优化算法主要是模拟了昆虫,兽群,鸟群和鱼群的群体行为,这些群体按照一定的合作方式寻找食物,群体中每个成员通过学习它自身经验和其他成员的经验来不断改变搜索的方向,任何一种由昆虫群体或者其他动物社会行为为机制而激发设计出的算法或者分 布式解释问题的策略均属于群体智能。
群体智能优化算法原组
- 邻近原则:群体能够进行简单的时间和空间计算
- 品质原则:群体能够影响环境中的品质因子
- 多样性反应原则:群体的行为范围冰不应该太窄
- 稳定性原则:群体不应再每次环境变化时都改变自身的行为
- 适应性原则:在所需要的代价不太高的情况下,群体能够在适当的时候,改变自身的行为
鸟群如何搜索食物
假设在搜索事务区域只有一块食物,所有的小鸟都不知道食物在什么地方,但是鸟儿之间存在互相交换信息,通过估计自身的适应度值,它们知道当前的位置距离食物还有多远,所以搜索目前食物最近的鸟的周围区域是找到食物的最简单有效的办法,通过鸟儿之间的集体协作使群体达到最优。
PSO与鸟群觅食
在PSO中每个优化问题的潜在解都可以想象成搜索空间中的一只鸟,我们称之为“粒子”,粒子主要追随当前的最优粒子在解空间中搜索,PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己,第一个粒子就是本身所找到的最优解,这个解叫做个体极值pbest,另一个极值就是整个群体目前找到的最优解,整个极值是全局极值gbest。由于粒子群优化算法中每个粒子在算法结束时仍然保持着其个体地极值,因此PSO用于调度和决策问题上可以给出多种有意义地选择方案。
粒子群算法的发展趋势
- 粒子群优化算法的改进:粒子群优化算法在解决空间函数的优化问题和单目标优化问题上应用比较多,如何应用于离散空间优化问题和多目标优化问题是粒子群优化算法的只要研究方向,如何充分结合其他进化类算法,发挥优势,改进粒子群优化算法的不足也值得研究。
- 粒子群优化算法的理论分析:粒子群优化算法提出时间不长,数学分析很不成熟和系统,存在许多不完善和未涉及的问题,对算法的运行行为,收敛性,计算复杂度的分析比较少,如何知道参数的选择和设计,如何设计适应值函数,如何提高算法在解空间搜索的效率算法收敛以及对算法模型本身的研究需要跟深入研究。
- 粒子群优化算法的应用:算法的有效性必须在应用中才能体现,广泛地开拓粒子群优化算法地应用领域,也对深入研究粒子群优化算法具有重要意义。
基本粒子群算法
1. 算法基本原理
PSO中,每个优化问题地潜在解都是搜索空间中地一只鸟,称之为粒子,所有粒子都有一个被优化地函数决定地适应值(fitness value),每个粒子还有一个速度决定它们飞行地方向和距离,然后粒子就追随当前地最优粒子在空间中搜索。粒子的更新方式:
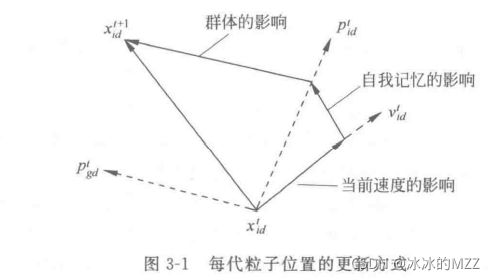

第一部分是惯性,反映粒子的运动习惯,代表粒子有维持自己先前速度的趋势
第二部分是认知部分,反映粒子对自身历史经验的记忆,代表粒子有向自己历史最佳位置逼近的趋势
第三部分是社会部分,反映粒子间协同合作和知识共享的群体历史经验,代表粒子有向群体或者邻域历史最佳位置逼近的趋势.
2. 算法构成要素
- 粒子群编码方式:基本粒子群算法使用固定长度的二进制符号串来表示群体中的个体,其等位基因是由二进制符号集{0,1}所组成,初始群体中各个个体的基因值可以随机生成。
- 个体适应度评价:通过确定局部最优迭代达到全局最优收敛,得出结果。
- 基本粒子群算法的运行参数
- r:粒子群算法的种子数,可以随机生成,也可以固定一个初始值。
- m:粒子群群体大小,一般取20-100,在变量多的时候可以取100以上
- max_d:一般为最大迭代次数以最小误差的要求满足,其也是终止条件数
- r1,r2:加速度权重系数
- c1,c2:加速度常数
- w:惯性系数
3. 算法参数设置
- 群体规模m:一般取20-40,试验表名,对于大多数问题来说,30个微粒就可以取得很好的结果,不过对于比较复杂的问题,也可以去100或者200,微粒越多,算法搜索的空间越大,也容易发现全局最优解,当然算法运行的时间也越长。
- 微粒长度l:即每个微粒的维数,由具体问题而定
- 微粒范围 [ − x m a x , x m a x ] [-x_{max},x_{max}] [−xmax,xmax]:由具体问题而定
- 微粒最大速度:微粒最大速度决定了在一次飞行中可以移动的最大距离,如果取得太大,可能会错 过好解,太小,微粒就不太容易进入局部最好解之外,而陷入局部最优解,通常 v m a x = k ∗ x m a x v_{max}=k*x_{max} vmax=k∗xmax,0.1<=k<=1。,每一维可以设置不同。
- 惯性权重: f w f_w fw通常设置为[0.2,1.2]。动态的惯性权重因子可以在PS搜索中线性变化,也可以根据某个测度函数而动态改变,一般采用Shi建议的线性递减权重策略: f w = f m a x − ( f m a x − f m i n ) / d m a x f_w=f_{max}-(f_{max}-f_{min})/d_{max} fw=fmax−(fmax−fmin)/dmax,其中 d m a x d_{max} dmax是最大进化代数, f m a x f_{max} fmax是初始惯性值, f m i n f_{min} fmin是迭代最大代数时的惯性权值,经典的分别取0.8和0.2。
- 加速度常数 c 1 , c 2 c_1,c_2 c1,c2:二者代表每个微粒的统计加速项的权重,低的值允许微粒在被拉回之前可以在目标区域外徘徊,而高的值则导致微粒突然冲向或者越过目标区域,一般取2,也可以取[0,4]之间,且二者相等。
4. 算法流程
i.初始化粒子群,包括群体规模N,每个粒子的速度 x i x_i xi和速度 v i v_i vi 。
ii. 计算每个粒子的适应度值Fit[i]。
iii. 对于每个粒子,用它的适应度值Fit[i]和个体极值 p b e s t ( i ) p_{best}(i) pbest(i)比较,如果前者大于后者,则用前者替换掉后者。
iv. 对于每个粒子,用它的适应度值Fit[i]和全局极值 g b e s t ( i ) g_{best}(i) gbest(i)比较,如果前者大于后者,则用前者替换掉后者。
v. 根据
![]()
跟新粒子的位置和速度
vi.如果满足结束条件如误差足够好或者达到迭代次数就退出,否则返回ii。
5. 算法例题:适应度函数 y = − ∑ i = 1 30 ( x i 2 + x i − 6 ) y=-\sum_{i=1}^{30}( x_i^2+x_i-6) y=−∑i=130(xi2+xi−6)
%PSO函数
function[xm,fv]=PSO(fitness,N,c1,c2,w,M,D)
% xm:目标函数取最小值时的自变量
% fv:目标函数的最小值
% fitness:待优化目标函数,即适应度函数
% N:粒子数目
% c1,c2:学习因子
% w:惯性权重
% M:最大迭代次数
% D:自变量个数(搜索空间维数)
% 此处显示详细说明
format long;
x=zeros(N,D);
v=zeros(N,D);
for i = 1:N
for j = 1:D
x(i,j)=randn;%初始化位置
v(i,j)=randn;%初始化速度
end
end
p=zeros(1,N);
y=zeros(N,D);
for i = 1:N
p(i)=fitness(x(i,:));%初始化每个粒子的适应度,假设当前位置的适应度为个体极值的适应度
y(i,:)=x(i,:);%初始化个体极值最大的位置
end
pg=x(N,:);
maxFit=p(N);
for i =1:(N-1)%初始化全局极值,找到适应度最大的粒子的位置。
if p(i)>maxFit
pg=x(i,:);
end
end
Pbest=zeros(1,M);
for t = 1:M%最大迭代次数
for i = 1:N
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
fit=fitness(x(i,:));
if fit>p(i)
p(i)=fit;%每次迭代保存当前个体的最大适应度。
y(i,:)=x(i,:);%每次迭代保存当前个体极值的位置。
end
if p(i)>maxFit
pg=y(i,:);%每次迭代寻找全局极值的位置
maxFit=p(i);%每次迭代寻找全局最大适应度
end
end
Pbest(t)=maxFit;%保存当次迭代的全局最大适应度
end
disp('****************************************************************');
disp('目标函数最大值时的位置');
xm = pg';
disp('目标函数的最大值为:');
fv=maxFit;
disp('*****************************************************************');
end
%适应度函数,即目标函数
function y = fun( x )
y=-sum(x.^2+x-6);
end
%调用
f=@fun;
[x,y]=PSO(f,30,1.5,2.5,0.5,50,30);%粒子数是30个,迭代次数是50次,维数是30
粒子群规模越大,运算得到的结果不一定精度越高,关键在于各个参数的合适搭配。