论文笔记:AAAI 2020 Learning Hierarchy-Aware Knowledge Graph Embeddings for Link Prediction
1. 前言
论文链接:https://arxiv.org/pdf/1911.09419.pdf
github:https://github.com/MIRALab-USTC/KGE-HAKE
HAKE 将实体映射到极坐标系中。 HAKE 受到这样一个事实的启发:极坐标系中的同心圆可以自然地反映层次结构。 具体来说,径向坐标旨在对层次结构不同级别上的实体进行建模,半径较小的实体应该位于较高的级别; 角坐标旨在区分层次结构相同级别的实体,并且这些实体的半径大致相同,但角度不同。 实验表明,HAKE可以有效地对知识图中的语义层次进行建模,并且明显优于现有的基准数据集上用于链接预测任务的最新方法。
2. 背景
许多现有的知识图谱嵌入方法无法在知识图中对语义层次进行建模。 但是在知识图谱中语义层次结构无处不在。
语义层次结构是知识图中普遍存在的属性。 例如,WordNet包含三元组[乔木/决明子/棕榈,上调,树],其中“树”在层次结构中比“乔木/决明子/棕榈”更高。 Freebase包含三元组[英格兰,/ location / location /包含,Pontefract / Lancaster],其中“ Pontefract / Lancaster”在层次结构中的级别低于“英格兰”。 尽管存在一些将层次结构考虑在内的工作,但他们通常需要额外的数据或过程来获取层次结构信息。 因此,寻找一种能够自动有效地对语义层次进行建模的方法仍然具有挑战性。
在本文中提出了一种新颖的知识图嵌入模型,即层次感知知识图嵌入(HAKE)。为了对语义层次进行建模,HAKE希望将实体分为两类:
- (a)在层次的不同级别
- (b)在等级的同一级别
受具有分层属性的实体可以看作数据结构中树的概念这一事实的启发,我们可以使用节点的深度(实体)来建模不同层次的层次结构。因此,我们使用模块化信息来建模类别(a)中的实体,其大小为模量可以反映深度。在上述设置下,类别(b)中的实体将具有大致相同的模数,这很难区分。受同一个圆上的点可以具有不同相位这一事实的启发,我们使用相位信息对类别(b)中的实体进行建模。结合模量和相位信息,HAKE将实体映射到极坐标系统,其中径向坐标对应于模量信息,而角度坐标对应于相位信息。
在本文中,分别使用小写字母 h h h , r r r 和 t t t 表示头实体,关系和尾实体。triplet ( h , r , t ) (h,r,t) (h,r,t) 表示事实。 相应的粗体小写字母 h h h, r r r 和 t t t 表示头部实体,关系和尾部实体的嵌入(矢量)。 向量 h h h 的第 i i i 个条目表示为 [ h ] i [h]_i [h]i。 令 k k k 表示嵌入尺寸。 让 ∘ : R n × R n → R n \circ:\mathbb{R}^n\times \mathbb{R}^n \rightarrow \mathbb{R}^n ∘:Rn×Rn→Rn表示两个向量之间的Hadamard乘积,即

∣ ∣ ⋅ ∣ ∣ 1 , ∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||_1,||\cdot||_2 ∣∣⋅∣∣1,∣∣⋅∣∣2 分别代表 L1 和 L2 正则化
本文提出的模型 HAKE 属于平移距离模型。 更具体地说, HAKE 与 RotatE 具有相似之处,RotatE作者声称它们同时使用了模数和相位信息。 但是,RotatE 和 HAKE 之间存在两个主要区别。 详细的区别如下:
- (a)目的不同。 RotatE 旨在对包括对称/反对称,反演和合成的关系模式进行建模。 HAKE 旨在对语义层次进行建模,同时还可以对上述所有关系模式进行建模。
- (b)使用模数信息的方式不同。 RotatE将关系建模为复杂空间中的旋转,无论关系是什么,这都会鼓励两个链接的实体具有相同的模数。 RotatE中的不同模量来自训练的不准确性。 取而代之的是,HAKE显式地对模量信息进行建模,在区分层次结构不同级别的实体方面,该信息明显优于RotatE。
另一个相关的问题是如何对知识图中的层次结构进行建模。 最近的一些工作以不同的方式考虑了这个问题。某些方法将实体和类别共同嵌入语义空间,并设计用于概念分类和无数据分层分类任务的模型。 其它一些方法使用聚类算法对层次关系结构建模。 同时还有方法提出了TKRL,将类型信息嵌入知识图嵌入。 也就是说,TKRL需要实体的其他分层类型信息。 与以前的工作不同,本文所提出的模型具有以下特点:
- (a)考虑链接预测任务,这是知识图嵌入中比较常见的任务;
- (b)无需使用聚类算法就可以自动学习知识图中的语义层次;
- (c)除了知识图中的三元组外,不需要任何其他信息。
3. HAKE
3.1 Two Categories of Entities
为了对知识图的语义层次进行建模,知识图嵌入模型必须能够区分以下两类中的实体:
- (a)层次结构中不同级别的实体。 例如,“哺乳动物”和“狗”,“奔跑”和“移动”。
- (b)处于同一等级的实体。 例如,“玫瑰”和“牡丹”,“货车”和“卡车”。
3.2 Hierarchy-Aware Knowledge Graph Embedding
为了对以上两个类别进行建模,本文提出了一种层次感知的知识图嵌入模型HAKE。 HAKE由两部分组成-模量部分和相位部分:分别旨在为两个不同类别中的实体建模。
图1给出了所提出模型的图示。为了区分不同部分的嵌入使用 e m e_m em( e e e 可以是 h h h 或 t t t)和 r m r_m rm 来表示实体嵌入和关系嵌入在模数部分中,并使用 e p e_p ep( e e e 可以是 h h h 或 t t t )和 r p r_p rp 来表示在阶段部分中进行实体嵌入和关系嵌入。
此外,我们可以期望层次结构较高级别的实体具有较小的模数,因为这些实体更接近树的根。 如果我们仅使用模数部分来嵌入知识图,则类别(b)中的实体将具有相同的模数。 此外,假设r是反映相同语义层次的关系,则[r] i将趋于为1,因为h? ? r = h对所有h成立。 因此,类别(b)中实体的嵌入趋于相同,这使得很难区分这些实体。 因此,需要一个新模块来对类别(b)中的实体进行建模。旨在对层次结构不同级别上的实体进行建模。受具有分层属性的实体可以看作一棵树这一事实的启发,我们可以使用节点的深度(实体)来对分层的不同级别进行建模。因此,我们使用模数信息来对类别(a)中的实体进行建模,因为模数可以反映树的深度。
具体而言,将 h m h_m hm 和 t m t_m tm 的每个条目(即 [ h m ] i [hm]_i [hm]i 和 [ t m ] i [tm]_i [tm]i)视为模数,并将 r m r_m rm 的每个条目(即 [ r ] i [r]_i [r]i)视为两个模量之间的比例转换。我们可以将模量部分公式如下:

相应的距离函数为:

模型允许实体嵌入的条目为负样本,但限制关系嵌入的条目为正样本。 这是因为实体嵌入的符号可以帮助我们预测两个实体之间是否存在关系。 例如,如果在 h h h 和 t 1 t_1 t1 之间存在关系 r r r,而在 h h h 和 t 2 t_2 t2 之间不存在关系,则 ( h , r , t 1 ) (h,r,t_1) (h,r,t1) 是正样本,而 ( h , r , t 2 ) (h,r,t_2) (h,r,t2) 是负样本 。 目标是最小化 d r ( h m , t 1 , m ) d_r(h_m,t_1,m) dr(hm,t1,m) 并最大化 d r ( h m , t 2 , m ) d_r(h_m,t_2,m) dr(hm,t2,m),以便在正样本和负样本之间做出明确区分。 对于正样本, [ h ] i [h]_i [h]i 和 [ t 1 ] i [t_1]_i [t1]i 倾向于共享相同的符号,因为 [ r m ] i > 0 [r_m]_i>0 [rm]i>0。对于负样本, [ h m ] i [h_m]_i [hm]i 和 [ t 2 , m ] i [t_{2,m}]_i [t2,m]i 的符号 如果我们随机初始化它们的符号,可能会有所不同。 这样, d r ( h m , t 2 , m ) d_r(h_m,t_2,m) dr(hm,t2,m) 可能会比 d r ( h m , t 1 , m ) d_r(h_m,t_1,m) dr(hm,t1,m) 大,这正是我们想要的。
此外,我们可以期望层次结构较高级别的实体具有较小的模数,因为这些实体更接近树的根。 如果我们仅使用模数部分来嵌入知识图,则类别(b)中的实体将具有相同的模数。 此外,假设 r r r 是反映相同语义层次的关系,则 [ r ] i [r]_i [r]i 将趋于为1,因为 h ∘ r ∘ r = h h \circ r \circ r = h h∘r∘r=h 对所有 h h h 成立。 因此,类别(b)中实体的嵌入趋于相同,这使得很难区分这些实体。 因此,需要一个新模块来对类别(b)中的实体进行建模。
阶段部分旨在在语义层次结构的相同级别上对实体进行建模。 受同一个圆上的点(即具有相同模数)可以具有不同相位这一事实的启发,我们使用相位信息来区分类别(b)中的实体。 具体地,我们将 h p h_p hp 和 t p t_p tp 的每个项,即 [ h p ] i [h_p]_i [hp]i 和 [ t p ] i [t_p]_i [tp]i 视为一个相位,并将 r p r_p rp 的每个项,即 [ r p ] i [r_p]_i [rp]i,作为相位变换。 阶段部分公式如下:

相应的距离函数为:
![]()
其中 s i n ( ⋅ ) sin(\cdot) sin(⋅) 是将正弦函数应用于输入的每个元素的运算。 注意,我们使用正弦函数来测量相位之间的距离,而不是使用 ∣ ∣ h p + r p − t p ∣ ∣ 1 ||h_p + r_p - t_p||_1 ∣∣hp+rp−tp∣∣1,因为相位具有周期性特征。
HAKE将模量部分和相位部分组合在一起,将实体映射到极坐标系中,其中径向坐标和角坐标分别对应于模量部分和相位部分。 也就是说,HAKE将实体 h h h 映射到 [ h m ; h p ] [h_m; h_p] [hm;hp],其中 h m h_m hm 和 h p h_p hp 分别由模量部分和相位部分以及 [ ⋅ ; ⋅ ] [·; ·] [⋅;⋅] 表示两个向量的串联。 显然, ( [ h m ] i , [ h p ] i ) ([h_m]_i,[h_p]_i) ([hm]i,[hp]i) 是极坐标系统中的二维点。 具体来说,HAKE公式如下:

HAKE的距离函数为:
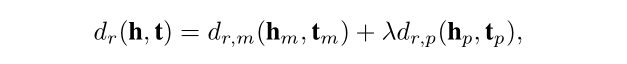
其中 λ ∈ R \lambda \in \mathbb{R} λ∈R 是模型学习到的参数。 相应的得分函数是:

当两个实体具有相同的模量时,模量部分 d r , m ( h m , t m ) = 0 d_{r,m}(h_m,t_m)=0 dr,m(hm,tm)=0。但是,相位部分 d r , p ( h p , t p ) d_{r,p}(h_p,t_p) dr,p(hp,tp) 可能非常不同。 通过组合模量部分和相位部分,HAKE可以对类别(a)和类别(b)中的实体进行建模。 因此,HAKE可以对知识图的语义层次进行建模。
在评估模型时,作何发现将混合偏差添加到 d r , m ( h , t ) d_{r,m}(h,t) dr,m(h,t)可以帮助改善HAKE的性能。 修改后的 d r , m ( h , t ) d_{r,m}(h,t) dr,m(h,t)由下式给出:

其中 − r m < r m ′ < 1 -r_m
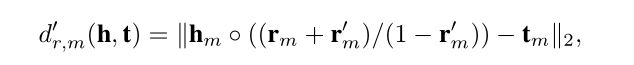
其中 / / / 表示按元素的除法运算。 如果我们令 r m ← ( r m + r m ′ ) / ( 1 − r m ′ ) r_m \leftarrow(r_m + r^{'}_m)/(1-r^{'}_m) rm←(rm+rm′)/(1−rm′),则当比较不同实体对的距离时,修改后的距离函数与原始函数完全相同。 为了表示方便,仍然使用 d r , m ( h , t ) = ∣ ∣ h m ∘ r m − t m ∣ ∣ 2 d_{r,m}(h,t)= ||h_m\circ r_m - t_m||_2 dr,m(h,t)=∣∣hm∘rm−tm∣∣2 代表模量部分。
3.3 Loss Function
训练模型,作者将负采样损失函数与自我对抗训练一起使用

其中 γ \gamma γ 是固定的超参数 , σ \sigma σ 是 sigmoid 函数, ( h i ′ , r , t i ′ ) (h^{'}_i,r,t^{'}_i) (hi′,r,ti′) 是第 i i i 个负三元组。 此外
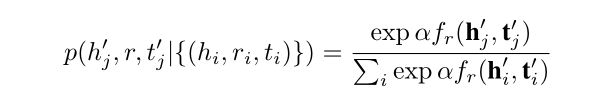
是采样负三元组的概率分布,其中 α \alpha α 是采样温度。


