《机器学习实战》——第10章 利用K-均值聚类算法对未标注数据分组

聚类是一种无监督的学习，它将相似的对象归到同一个簇中。它有点像全自动分类。聚类方法几乎可以应用于所有对象，簇内的对象越相似，聚类的效果越好。
簇识别给出聚类结果的含义。假定有一些数据，现在将相似数据归到一起，簇识别会告诉我们这些簇到底都是些什么。聚类与分类的最大不同在于，分类的目标事先已知，而聚类则不一样。因为其产生的结果与分类相同，而只是类别没有预先定义，聚类有时也被称为无监督分类。
聚类分析试图将相似对象归入同一簇，将不相似对象归到不同簇。相似这一概念取决于所选择的相似度计算方法。
下面会构建K-均值方法并观察其实际效果。接下来还会讨论简单K-均值算法中的一些缺陷。为了解决其中的一些缺陷，可以通过后处理来产生更好的簇。接着会给出一个更有效的称为二分K-均值的聚类算法。

10.1 K-均值聚类算法

K-均值聚类
优点：容易实现。
缺点：可能收敛到局部最小值，在大规模数据集上收敛较慢。
适用数据类型：数值型数据。

K-均值是发现给定数据集的k个簇的算法。簇个数k是用户给定的，每一个簇通过其质心，即簇中所有点的中心来描述。
K-均值算法的工作流程：首先，确定随机k个初始点作为质心。然后将数据集中的每个点分配到一个簇中，具体来讲，为每个点找距其最近的质心，并将其分配给该质心所对应的簇。这一步完成之后，每个簇的质心更新为该簇所有点的平均值。伪代码如下：

 “最近”质心意味着需要进行某种距离计算。数据集上K-均值算法的性能会受到所选距离计算方法的影响。下面给出K-均值算法的代码实现。首先创建一个名为kMeans.py的文件，然后将下面的代码加入其中：

from numpy import *

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float,curLine)) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat

def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(list(dataSet[:,j]))
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids

代码中包含几个K-均值算法中要用到的辅助函数。第一个函数loadDataSet()和上一章完全相同，它将文本文件导入到一个列表中。文本文件每一行为tab分隔的浮点数。每一个列表会被添加到dataMat中，最后返回dataMat。该返回值是一个包含许多其他列表的列表。这种格式可以很容易将很多值封装到矩阵中。
下一个函数 distEclud() 计算两个向量的欧氏距离。这是本章最先使用的距离函数，也可以使用其他距离函数。
最后一个函数是 randCent() ，该函数为给定数据集构建一个包含k个随机质心的集合。随机质心必须要在整个数据集的边界之内，这可以通过找到数据集每一维的最小和最大值来完成。然后生成0到1.0之间的随机数并通过取值范围和最小值，以便确保随机点在数据的边界之内。

import kMeans
from numpy import *
datMat = mat(kMeans.loadDataSet('testSet.txt'))
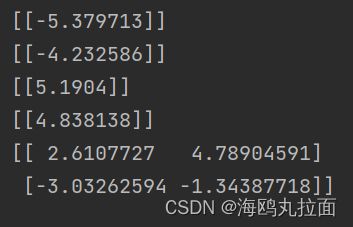
print(min(datMat[:,0]))
print(min(datMat[:,1]))
print(max(datMat[:,1]))
print(max(datMat[:,0]))

使用 randCent() 函数生成min到max之间的值：

import kMeans
from numpy import *
datMat = mat(kMeans.loadDataSet('testSet.txt'))
print(min(datMat[:,0]))
print(min(datMat[:,1]))
print(max(datMat[:,1]))
print(max(datMat[:,0]))
print(kMeans.randCent(datMat,2))

可以看到函数 randCent() 生成min到max之间的值。下面测试一下距离计算方法：

print(kMeans.distEclud(datMat[0],datMat[1]))

函数均正常运行，可以准备实现完整K-均值算法。该算法会创建k个质心，然后将每个点分配到最近的质心，再重新计算质心。这个过程重复数次，直到数据点的簇分配结果不再改变为止。为kMeans.py文件加入下面的代码：

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))#create mat to assign data points
                                      #to a centroid, also holds SE of each point
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):#for each data point assign it to the closest centroid
            minDist = inf; minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print(centroids)
        for cent in range(k):#recalculate centroids
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean
    return centroids, clusterAssment

代码给出了K-均值算法，kMeans() 函数接受4个输入参数。只有数据集及簇的数目是必选参数，而用来计算距离和创建初始质心的函数都是可选的。kMeans() 函数一开始确定数据集中数据点的总数，然后创建了一个矩阵来存储每个点的簇分配结果。簇分配结果矩阵clusterAssment包含两列：一列记录簇索引值，第二列存储误差。误差是指当前点到簇质心的距离，后面会使用该误差来评价聚类效果。
按照计算质心——分配——重新计算反复迭代，直到所有数据点的簇分配结果不再改变为止。程序中可以创建一个标志变量clusterChanged，如果该值为True，则继续迭代。上述迭代使用while循环来实现。接下来遍历所有数据找到距离每个点最近的质心，这可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成。计算距离是使用distMeans参数给出的距离函数，默认距离函数是 distEclud() ，该函数的实现已经给出。如果任一点的簇分配结果发生改变，则更新clusterChanged标志。
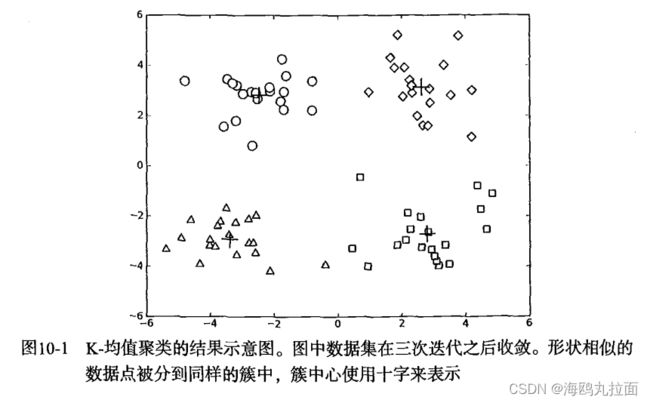
最后，遍历所有质心并更新它们的取值。步骤如下：首先通过数组过滤来获得给定簇的所有点；然后计算所有点的均值，选项 axis=0 表示沿矩阵的列方向进行均值计算；最后，程序返回所有的类质心与点分配结果。下图给出了一个聚类结果的示意图。

import kMeans
from numpy import *
datMat = mat(kMeans.loadDataSet('testSet.txt'))
myCentroids,clustAssing = kMeans.kMeans(datMat,4)

运行结果给出了4个簇（质心），经过3次迭代后K-均值算法收敛。

10.2 使用后处理来提高聚类性能

K-均值聚类中簇的数目k是一个用户预先定义的参数，那么用户如何才能知道k的选择是否正确？如何才能知道生成的簇比较好？在包含簇分配结果的矩阵中保存着每个点的误差，即该点到簇质心的距离平方值。
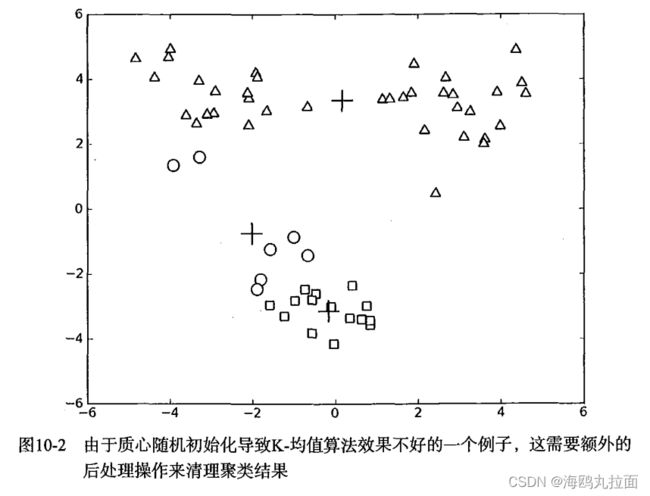
考虑下图中的聚类结果，这是在一个包含三个簇的数据集上运行K-均值算法之后的结果，但是点的簇分配结果值没有那么准确。K-均值算法收敛但聚类效果较差的原因是，K-均值算法收敛到了局部最小值，而非全局最小值（局部最小值指结果还可以但非最好结果，全局最小值是可能的最好结果）。
一种用于度量聚类效果的指标是SSE（误差平方和），对应程序中clusterAssment矩阵的第一列之和。SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。因为对误差取了平方，因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
那么如何对下图结果进行改进？可以对生成的簇进行后处理，一种方法是将具有最大SSE值的簇划分成两个簇。具体实现时可以将最大簇包含的点过滤出来并在这些点上运行K-均值算法，其中的k设为2。

为了保持簇总数不变，可以将某两个簇进行合并。图中可以明显看出，应该将下部两个出错的簇质心进行合并。可以很容易对二位数据上的聚类进行可视化，但如果遇到更高维数据该如何去做？
有两种可以量化的方法：合并最近的质心，或者合并两个使得SSE增幅最小的质心。第一种思路通过计算所有质心之间的距离，然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总SSE值。必须在所有可能的两个簇上重复上述处理过程，知道直到合并最佳的两个簇为止。

10.3 二分K-均值算法

为克服K-均值算法收敛于局部最小值的问题，有人提出另一个称为二分K-均值的算法。该算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续进行划分，选择哪一个簇机芯划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。
二分K-均值算法伪代码形式如下：

将所有点看成一个簇
当簇数目小于k时
对于每一个簇
   计算总误差
   在给定的簇上面进行K-均值聚类(k=2)
   计算将该簇一分为二之后的总误差
选择使得误差最小的那个簇进行划分操作

另一种做法是选择SSE最大的簇进行划分，直到簇数目达到用户指定的数目为止。打开kMeans.py加入下面的代码：

def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList =[centroid0] #create a list with one centroid
    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
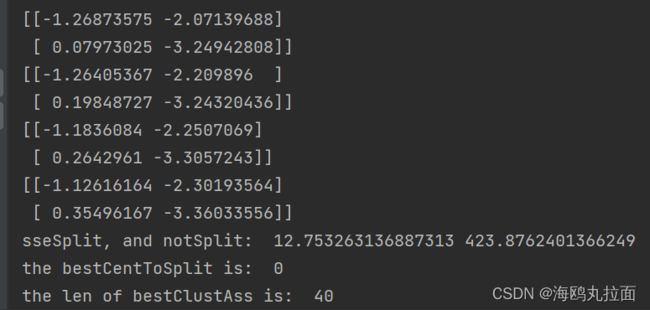
            print("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print('the bestCentToSplit is: ',bestCentToSplit)
        print('the len of bestClustAss is: ', len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE
    return mat(centList), clusterAssment

上述程序中的函数与 kMeans() 的参数相同。在给定数据集、所期望的簇数目和计算方法的条件下，函数返回聚类结果。同 kMeans() 一样，用户可以改变所使用的距离计算方法。
该函数首先创建一个矩阵来存储集中在每个点的簇分配结果及平方误差，然后计算整个数据集的质心，并使用一个列表来保留所有的质心。得到上述质心之后，可以遍历数据集中所有点来计算每个点到质心的误差值。
接下来程序进入while循环，该循环会不停对簇进行划分，直到得到想要的簇数目为止。可以通过考察簇列表中的值来获得当前簇的数目。然后遍历所有的簇来决定最佳的簇进行划分。为此需要比较划分前后的SSE。一开始将最小SSE设置成无穷大，然后遍历簇列表cenList中的每一个簇。对每个簇，将该簇中的所有点砍成一个小的数据集ptsInCurrCluster。将ptsInCurrCluster输入到函数 kMeans() 中进行处理（k=2）。K-均值算法会生成两个质心（簇），同时给出每个簇的误差值。这些误差与剩余数据集的误差之和作为本次划分的误差。如果该划分的SSE值最小，则本次划分被保存。一旦决定了要划分的簇，接下来就要实际执行划分操作。划分操作很容易，只需要将要划分的簇中的所有点的簇分配结果进行修改即可。当使用 kMeans() 函数并且指定簇树为2时，会得到两个编号分别为0和1的结果簇。需要将这些簇编号修改为划分簇及新加簇的编号，该过程可以通过两个数组过滤器来完成。最后，新的簇分配结果被更新，新的质心会被添加到cenList中。
当while循环结束时，同 kMeans() 函数一样，函数返回质心列表与簇分配结果。

import kMeans
from numpy import *
datMat3 = mat(kMeans.loadDataSet('testSet2.txt'))
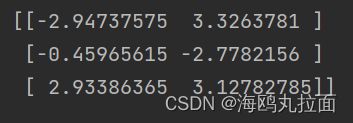
cenList,myNewAssments = kMeans.biKmeans(datMat3,3)

查看质心结果：

 

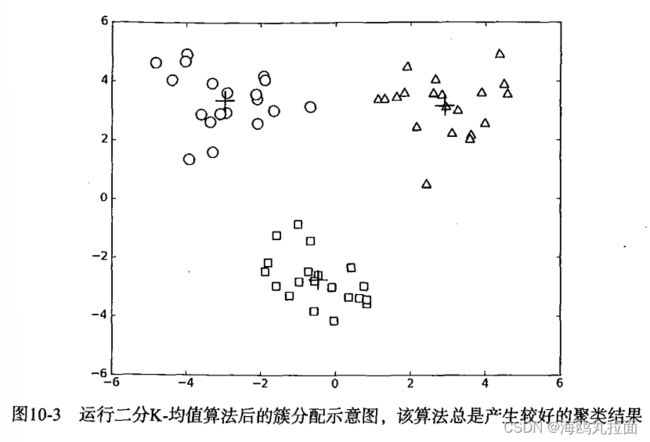
上述函数可以运行多次，聚类会收敛到全局最小值，而原始的 kMeans() 函数偶尔会陷入局部最小值。下图给出了数据集及运行 biKmeans() 后的质心的示意图。