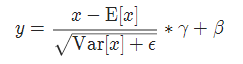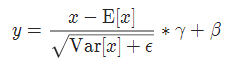深度学习中的归一化方法BN,LN,IN,GN
文章目录
- 前言
- 一、BN
- 二、LN
- 三、IN
- 四、GN
前言
归一化层,目前主要有这几个方法,
1、Batch Normalization(2015)
2、Layer Normalization(2016)
3、Instance Normalization(2017)
4、Group Normalization(2018)
区别:

将输入的图像shape记为[N, C, H, W],这几个方法主要的区别就是在:
Batch Norm是在batch上,对NHW做归一化,就是对每个单一通道输入进行归一化,这样做对小batchsize效果不好;
Layer Norm在通道方向上,对CHW归一化,就是对每个深度上的输入进行归一化,主要对RNN作用明显;
Instance Norm在图像像素上,对HW做归一化,对一个图像的长宽即对一个像素进行归一化,用在风格化迁移;
Group Norm将channel分组,有点类似于LN,只是GN把channel也进行了划分,细化,然后再做归一化;
Switchable Norm是将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
以上摘自https://blog.csdn.net/qq_41997920/article/details/89945972?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163927665316780265454206%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=163927665316780265454206&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v1~rank_v31_ecpm-1-89945972.first_rank_v2_pc_rank_v29&utm_term=Layer+Norm%EF%BC%8CGroup+Norm&spm=1018.2226.3001.4187
一、BN
我们在对数据训练之前会对数据集进行归一化,归一化的目的归一化的目的就是使得预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而偏差大的样本数据导致的不良影响,而且数据如果偏差大,我们设置学习率就要很小,这样会降低训练速度;另外统一数据规模可以让机器更容易学习。
虽然输入层的数据,已经归一化,后面网络每一层的输入数据的分布一直在发生变化,前面层训练参数的更新将导致后面层输入数据分布的变化,必然会引起后面每一层输入数据分布的改变。而且,网络前面几层微小的改变,后面几层就会逐步把这种改变累积放大。训练过程中网络中间层数据分布的改变称之为:“Internal Covariate Shift(内部协方差漂移)”。BN的提出,就是要解决在训练过程中,中间层数据分布发生改变的情况。所以就引入了BN的概念,来消除这种影响。
另外,如果在每一层加入激活函数,以sigmoid为例,当横轴趋向于无穷大时梯度会消失,用BN层可以将偏差大的数据拉回0附近的梯度敏感地带,所以在每次传入网络的数据每一层的网络都进行一次BN,将数据拉回正态分布,这样做使得数据分布一致且避免了梯度消失。
此外,internal corvariate shift和covariate shift是两回事,前者是网络内部,后者是针对输入数据,比如我们在训练数据前做归一化等预处理操作。
需要注意的是在使用小batch-size时BN会破坏性能,当具有分布极不平衡二分类任务时也会出现不好的结果,分布不均的分类任务也会出现这种情况。因为BN计算每一个batch的期望和标准差,我们希望的是计算出来的期望和标准差能代表整个数据上的分布规律,如果小的batch-size归一化,可能会和整体差别较大,均值和方差不足以代替整个数据分布。
BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他sequence长很多,这样training时,计算很麻烦。
总结:
1、有BN层时,学习率不一定设置的非常小;
2、梯度消失可以被解决;
3、初始化对参数的影响小了,因为如果初始化偏差较大,经过BN也会拉回一个正常范围。
4、有解决过拟合的效果,假设有噪声也会被归一化。
pytorch实现torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
num_features: 来自期望输入的特征数,该期望输入的大小为’batch_size x num_features [x width]’
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
momentum: 动态均值和动态方差所使用的动量。默认为0.1。
affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
track_running_stats:布尔值,当设为true,记录训练过程中的均值和方差;
手动实现:
x_shape:[B, C, H, W],则计算第0、2、3轴的方差和均值。
import numpy as np
def Batchnorm(x, gamma, beta, bn_param):
# x_shape:[B, C, H, W]
running_mean = bn_param['running_mean']
running_var = bn_param['running_var']
results = 0.
eps = 1e-5
x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
# 因为在测试时是单个图片测试,这里保留训练时的均值和方差,用在后面测试时用
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return results, bn_param
二、LN
与BN不同的是,LN对每一层的所有神经元进行归一化;
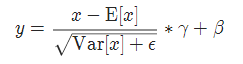
LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
pytorchtorch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
normalized_shape: 输入尺寸
[∗×normalized_shape[0]×normalized_shape[1]×…×normalized_shape[−1]]
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
elementwise_affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
手动实现:
x_shape:[B, C, H, W],则计算第1、2、3轴的方差和均值。
def Layernorm(x, gamma, beta):
# x_shape:[B, C, H, W]
results = 0.
eps = 1e-5
x_mean = np.mean(x, axis=(1, 2, 3), keepdims=True)
x_var = np.var(x, axis=(1, 2, 3), keepdims=True0)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
return results
三、IN
BN注重对每一个batch进行归一化,保证数据分布的一致,因为判别模型中的结果取决与数据的整体分布。在图像风格中,生成结果主要依赖某个图像实例,所以此时对整个batch归一化不适合了,需要对但像素进行归一化,可以加速模型的收敛,并且保持每个图像实例之间的独立性!
在目前的GAN和style transfer的任务中,目前的IN norm要好于BN,IN主要用于对单张图像的数据做处理,而BN主要是对Bacth的数据做处理。由于BN在训练时每个batch的均值和方差会由于shuffle都会改变,所以可以理解为一种数据增强,而IN可以理解为对数据做一个归一化的操作。
换句话说,BN的计算是要受其他样本影响的,由于每个batch的均值和标准差不稳定,对于单个数据而言,相对于是引入了噪声,但在分类这种问题上,结果和数据的整体分布有关系,因此需要通过BN获得数据的整体分布。而instance norm的信息都是来自于自身的图片,相当于对全局信息做了一次整合和调整,在图像转换这种问题上,BN获得的整体信息不会带来任何收益,带来的噪声反而会弱化实例之间的独立性。
总而言之,对于分类这种high level的问题,使用BN优于IN, 对于Low level问题,IN优于BN。
pytorch实现:torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
num_features: 来自期望输入的特征数,该期望输入的大小为’batch_size x num_features [x width]’
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
momentum: 动态均值和动态方差所使用的动量。默认为0.1。
affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
track_running_stats:布尔值,当设为true,记录训练过程中的均值和方差;
手动实现:
def Instancenorm(x, gamma, beta):
# x_shape:[B, C, H, W]
results = 0.
eps = 1e-5
x_mean = np.mean(x, axis=(2, 3), keepdims=True)
x_var = np.var(x, axis=(2, 3), keepdims=True0)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
return results
四、GN
Group Normalization(GN)是针对Batch Normalization(BN)在batch size较小时错误率较高而提出的改进算法,因为BN层的计算结果依赖当前batch的数据,当batch size较小时(比如1、2、4这样),该batch数据的均值和方差的代表性较差,因此对最后的结果影响也较大, GN将channel方向分group,然后每个group内做归一化,算(C//G)HW的均值,这样与batchsize无关,不受其约束。
pytorch实现:torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)
num_groups:需要划分为的groups
num_features: 来自期望输入的特征数,该期望输入的大小为’batch_size x num_features [x width]’
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
momentum: 动态均值和动态方差所使用的动量。默认为0.1。
affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
手动实现:
def GroupNorm(x, gamma, beta, G=16):
# x_shape:[B, C, H, W]
results = 0.
eps = 1e-5
x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))
x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
return results