深度强化学习CS285 lec13-lec15 (中)
Soft Optimality
- 概述
- 一、概率图基础知识
- 二、Soft Optimality Framework
-
- 2.1 Recap
- 2.2 Soft Optimality与Value Iteration的联系
- 2.3 Optimism Problem(关键哦!)
-
- 2.3.1 Optimism问题的引出
- 2.3.2 Soft与Standard RL的区别
- 2.3.3 Deterministic dynamics的Objective
- 2.3.4 Stochastic Dynamics的Objective
- 2.4 Soft Value Iteration
- 2.5 Soft Q-leanring
- 2.6 Policy Gradient with Soft Optimality
- 2.7 Soft Actor-Critic
- 三、Summary
- 后记
概述
-
目标理解:
- 给定Objective,找出Policy;相似说法为给定Intent,找出一个Optimal behavior
- 给定Stochastic Optimal Behavior,推断其Intent;相似说法为给定expert demonstrations,推断其Objective
-
Intuition:
- Soft Optimality也称为Stochastic Optimal Control ,是对Stochastic Optimal Behavior进行建模,引入二值Optimality Variable
- 一些mistakes更重要,但没必要一直Optimal,在Intent可Reach的情况下,允许做一些Sub-Optimal的事,去explore一下
- 使用PGM for decision making会解释一下,为什么good behavior确实会好过bad behavior以及同为good behavior的时候,有同样的概率reach goal。(slightly random slightly different)
-
问题描述:
- 如何在模型中加入Intent?(Optimality Variable)
- O t = 1 O_t=1 Ot=1 是trying to be optimal的变量,表达了一种intent的意图而不是实际的最优,只是希望最优的意图intent, O t = 0 O_t=0 Ot=0可以理解成做随机策略的意思,所以有 p ( τ ∣ O 1 : T ) p(\tau|O_{1:T}) p(τ∣O1:T)表示Generative Model Of Optimal Behavior即每时每刻都维持这个最优的intent,会产生什么样的轨迹。
- 选择 p ( O t ∣ s t , a t ) = e x p ( r ( s t , a t ) ) p(O_t|s_t,a_t)=exp(r(s_t,a_t)) p(Ot∣st,at)=exp(r(st,at)),这个intent应该是跟reward有关的,reward大的地方intent就更强烈~
- 这个Stochastic Behavior model,可以对Sub-Optimal的动作建模,但并不具备推理的能力
一、概率图基础知识
在概率图PGM中,Inference有如下几类,已知n维观测对象 { x 1 , . . . , x n } \{x_1,...,x_n\} {x1,...,xn},k维状态对象 { z 1 , . . . , z k } \{z_1,...,z_k\} {z1,...,zk},引入时间维度后,有 X = { X 1 , . . , X T } , { Z 1 , . . . , Z T } X=\{X_1,..,X_T\},\{Z_1,...,Z_T\} X={X1,..,XT},{Z1,...,ZT}.
- Learning:学习模型的参数 λ \lambda λ
λ ∗ = arg max λ P ( X ∣ λ ) \lambda^*=\argmax_\lambda P(X|\lambda) λ∗=λargmaxP(X∣λ) - Inference:已知模型的参数 λ \lambda λ,去Inference一些变量
- Decoding:给定观测序列 X X X,预测隐状态序列 Z Z Z
Z = arg max Z P λ ( Z ∣ X ) Z 1 , . . , Z t = arg max Z P λ ( Z 1 , . . . , Z t ∣ X 1 , . . . , X t ) Z=\argmax_ZP_\lambda(Z|X)\\ Z_1,..,Z_t=\argmax_ZP_\lambda(Z_1,...,Z_t|X_1,...,X_t) Z=ZargmaxPλ(Z∣X)Z1,..,Zt=ZargmaxPλ(Z1,...,Zt∣X1,...,Xt) - Evidence:出现观测序列的概率
p λ ( X ) = p λ ( X 1 , . . . , X T ) p_{\lambda}(X)=p_\lambda(X_1,...,X_T) pλ(X)=pλ(X1,...,XT) - Filtering :给定当前时刻前的历史信息,预测当前时刻的隐状态
P ( Z t ∣ X 1 , . . . , X t ) P(Z_t|X_1,...,X_t) P(Zt∣X1,...,Xt) - Smoothing:给定所有信息,复盘一下某时刻的隐状态
P ( Z t ∣ X 1 , . . . , X T ) P(Z_t|X_1,...,X_T) P(Zt∣X1,...,XT) - Prediction:给定当前时刻前的历史信息,预测下一时刻的观测变量或者隐状态
P ( Z t + 1 ∣ X 1 , X 2 , . . . , X t ) P ( X t + 1 ∣ X 1 , X 2 , . . . , X t ) P(Z_{t+1}|X_1,X_2,...,X_t)\\ P(X_{t+1}|X_1,X_2,...,X_t) P(Zt+1∣X1,X2,...,Xt)P(Xt+1∣X1,X2,...,Xt)
- Decoding:给定观测序列 X X X,预测隐状态序列 Z Z Z
二、Soft Optimality Framework
2.1 Recap
在lec13-lec15 (上)中有
- Soft Optimality
- Forward
α t ( s t ) = p ( s t ∣ O 1 : t − 1 ) \alpha_t(s_t)=p(s_t|O_{1:t-1}) αt(st)=p(st∣O1:t−1) - Backward
β t ( s t , a t ) = p ( O t : T ∣ s t , a t ) \beta_t(s_t,a_t)=p(O_{t:T}|s_t,a_t) βt(st,at)=p(Ot:T∣st,at) - Policy
π ( a t ∣ s t ) = p ( a t ∣ s t , O 1 : T ) = β t ( s t , a t ) β t ( s t ) p ( s t ∣ O 1 : T ) ∝ β t ( s t ) α t ( s t ) \pi(a_t|s_t)=p(a_t|s_t,O_{1:T})=\frac{\beta_t(s_t,a_t)}{\beta_t(s_t)}\\ p(s_t|O_{1:T})\propto \beta_t(s_t)\alpha_t(s_t) π(at∣st)=p(at∣st,O1:T)=βt(st)βt(st,at)p(st∣O1:T)∝βt(st)αt(st) - Optimality Variable p ( O t = 1 ∣ s t , a t ) = e x p ( r ( s t , a t ) ) p(O_t=1|s_t,a_t)=exp(r(s_t,a_t)) p(Ot=1∣st,at)=exp(r(st,at))
解释一下:
- β t ( s t , a t ) = p ( O t : T ∣ s t , a t ) \beta_t(s_t,a_t)=p(O_{t:T}|s_t,a_t) βt(st,at)=p(Ot:T∣st,at):如果在该state和action下,我需要一直optimal才能维持intent可reach的概率
- p ( a t ∣ s t , O 1 : T ) p(a_t|s_t,O_{1:T}) p(at∣st,O1:T):给定我一直要维持intent即 O 1 : T = 1 O_{1:T}=1 O1:T=1,在某个state下,可以做哪些action的概率
- α t ( s t ) = p ( s t ∣ O 1 : t − 1 ) \alpha_t(s_t)=p(s_t|O_{1:t-1}) αt(st)=p(st∣O1:t−1):如果我之前一直在optimal,那我会reach到哪个state的概率
- p ( O t = 1 ∣ s t , a t ) ∝ e x p ( r ( s t , a t ) ) p(O_t=1|s_t,a_t)\propto exp(r(s_t,a_t)) p(Ot=1∣st,at)∝exp(r(st,at)):这个Optimality Variable是对Intent进行建模,在当前 s t , a t s_t,a_t st,at条件下,是否需要维持Optimal这个Intent正比于 r ( s t , a t ) r(s_t,a_t) r(st,at)
- p ( s t ∣ O 1 : T ) ∝ β t ( s t ) α t ( s t ) p(s_t|O_{1:T})\propto\beta_t(s_t)\alpha_t(s_t) p(st∣O1:T)∝βt(st)αt(st):给定一直维持Optimal Intent的情况下,到达某时刻state的概率正比于 p ( s t ∣ O 1 : t − 1 ) p ( O t : T ∣ s t ) p(s_t|O_{1:t-1})p(O_{t:T}|s_t) p(st∣O1:t−1)p(Ot:T∣st)
2.2 Soft Optimality与Value Iteration的联系
-
Backward Process:
β t ( s t , a t ) = p ( O t ∣ s t , a t ) E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ β t + 1 ( s t + 1 ) ] β t ( s t ) = E a t ∼ p ( a t ∣ s t ) [ β t ( s t , a t ) ] \beta_t(s_t,a_t)=p(O_{t}|s_t,a_t)E_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}\Big[\beta_{t+1}(s_{t+1})\Big]\\ \beta_t(s_t)=E_{a_{t}\sim p(a_{t}|s_{t})}\Big[\beta_t(s_t,a_t)\Big] βt(st,at)=p(Ot∣st,at)Est+1∼p(st+1∣st,at)[βt+1(st+1)]βt(st)=Eat∼p(at∣st)[βt(st,at)] -
Soft Optimality的Backward Process通过变换会与Model-free中熟悉的Value Iteration建立联系(Soft Value Iteration)
L e t β t ( s t ) = e x p ( V t ( s t ) ) , L e t β t ( s t , a t ) = e x p ( Q t ( s t , a t ) ) Let\quad \beta_t(s_t)=exp(V_t(s_t)),Let \quad \beta_t(s_t,a_t)=exp(Q_t(s_t,a_t)) Letβt(st)=exp(Vt(st)),Letβt(st,at)=exp(Qt(st,at))
1. Q t ( s t , a t ) = r ( s t , a t ) + l o g E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ e x p ( V t ( s t + 1 ) ) ] 2. V t ( s t ) = l o g E a t ∼ p ( a t ∣ s t ) [ e x p ( Q t ( s t , a t ) + l o g p ( a t ∣ s t ) ) ⏟ a c t i o n p r i o r ] \begin{aligned} &1.\quad Q_t(s_t,a_t)=r(s_t,a_t)+logE_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}\Big[exp(V_t(s_{t+1}))\Big]\\ &2.\quad V_t(s_t)=logE_{a_{t}\sim p(a_{t}|s_{t})}\Big[\underbrace{exp\big(Q_t(s_t,a_t)+logp(a_t|s_t)\big)}_{action\quad prior}\Big] \end{aligned} 1.Qt(st,at)=r(st,at)+logEst+1∼p(st+1∣st,at)[exp(Vt(st+1))]2.Vt(st)=logEat∼p(at∣st)[actionprior exp(Qt(st,at)+logp(at∣st))]按照如下policy的公式做出决策:
π ( a t ∣ s t ) = β t ( s t , a t ) β t ( s t ) = e x p ( Q t ( s t , a t ) ) e x p ( V t ( s t ) ) = e x p ( Q t ( s t , a t ) − V t ( s t ) ) = e x p ( A t ( s t , a t ) ) \pi(a_t|s_t)=\frac{\beta_t(s_t,a_t)} {\beta_t(s_t)}=\frac{exp(Q_t(s_t,a_t))}{exp(V_t(s_t))}=exp(Q_t(s_t,a_t)-V_t(s_t))=exp(A_t(s_t,a_t)) π(at∣st)=βt(st)βt(st,at)=exp(Vt(st))exp(Qt(st,at))=exp(Qt(st,at)−Vt(st))=exp(At(st,at)) -
传统的Value Iteration
- Q ( s , a ) = r ( s , a ) + E s ′ ∼ p ( s ′ ∣ s , a ) [ V ( s ′ ) ] Q(s,a)=r(s,a)+ E_{s'\sim p(s'|s,a)}[V(s')] Q(s,a)=r(s,a)+Es′∼p(s′∣s,a)[V(s′)]
- V ( s ) = max a Q ( s , a ) V(s)=\max_a Q(s,a) V(s)=maxaQ(s,a)
按照如下policy的公式做出决策:
π ( a t ∣ s t ) = δ ( a = arg max a t Q ( s t , a t ) ) , δ \pi(a_t|s_t)=\delta(a=\argmax_{a_t}Q(s_t,a_t)),\delta π(at∣st)=δ(a=atargmaxQ(st,at)),δ可为greedy policy的一个函数。
2.3 Optimism Problem(关键哦!)
2.3.1 Optimism问题的引出
action prior一般假设是均匀的,于是Soft Value Iteration变成如下:
1. Q t ( s t , a t ) = r ( s t , a t ) + l o g E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ e x p ( V t ( s t + 1 ) ) ] 2. V t ( s t ) = l o g ∫ [ e x p ( Q t ( s t , a t ) ) ] d a t \begin{aligned} &1.\quad Q_t(s_t,a_t)=r(s_t,a_t)+logE_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}\Big[exp(V_t(s_{t+1}))\Big]\\ &2.\quad V_t(s_t)=log\int\Big[exp\big(Q_t(s_t,a_t)\big)\Big]da_t \end{aligned} 1.Qt(st,at)=r(st,at)+logEst+1∼p(st+1∣st,at)[exp(Vt(st+1))]2.Vt(st)=log∫[exp(Qt(st,at))]dat
对于第二步, V t ( s t ) = l o g ∫ [ e x p ( Q t ( s t , a t ) ) ] d a t V_t(s_t)=log\int\Big[exp\big(Q_t(s_t,a_t)\big)\Big]da_t Vt(st)=log∫[exp(Qt(st,at))]dat,当某个 a t a_t at的值较大时,根据exp平滑的特性,有 l o g ∫ [ e x p ( Q t ( s t , a t ) ) ] d a t → m a x a Q ( s t , a t ) log\int\Big[exp\big(Q_t(s_t,a_t)\big)\Big]da_t\rightarrow max_a Q(s_t,a_t) log∫[exp(Qt(st,at))]dat→maxaQ(st,at),与传统VI第二步差不多
对于第一步, Q t ( s t , a t ) = r ( s t , a t ) + l o g E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ e x p ( V t ( s t + 1 ) ) ] Q_t(s_t,a_t)=r(s_t,a_t)+logE_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}\Big[exp(V_t(s_{t+1}))\Big] Qt(st,at)=r(st,at)+logEst+1∼p(st+1∣st,at)[exp(Vt(st+1))]当下一状态的value大时,根据exp平滑拉大差距的特性,就与传统VI第一步相差远了 Q ( s , a ) = r ( s , a ) + E s ′ ∼ p ( s ′ ∣ s , a ) [ V ( s ′ ) ] Q(s,a)=r(s,a)+ E_{s'\sim p(s'|s,a)}[V(s')] Q(s,a)=r(s,a)+Es′∼p(s′∣s,a)[V(s′)]。
==这样会出现一个Optimism的问题,当下一状态是deterministic的时候无所谓,毕竟下一状态是确定的,有
Q t ( s t , a t ) = r ( s t , a t ) + l o g E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ e x p ( V t ( s t + 1 ) ) ] = r ( s t , a t ) + V t + 1 ( s t + 1 ) Q_t(s_t,a_t)=r(s_t,a_t)+logE_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}\Big[exp(V_t(s_{t+1}))\Big]=r(s_t,a_t)+V_{t+1}(s_{t+1}) Qt(st,at)=r(st,at)+logEst+1∼p(st+1∣st,at)[exp(Vt(st+1))]=r(st,at)+Vt+1(st+1)
但当下一状态是stochastic的时候会出现Optimism问题,即若 E [ V ( s ′ ) ] E[V(s')] E[V(s′)]的expected Value是中间的值,但下一状态Value的分布是一高一低,则 E [ e x p ( V ( s ′ ) ) ] E[exp(V(s'))] E[exp(V(s′))]则会向高的值,导致risk-seeking behavior,这个就是Optimism的问题,那为什么会这样呢?
2.3.2 Soft与Standard RL的区别
因为这个Soft Framework的出发角度与之前standard RL是不一样的!
在Standard RL中,是给定一个Objective:
θ ∗ = arg max θ E τ ∼ p θ ( τ ) [ r ( τ ) ] = arg max π E s t ∼ p ( s t ∣ s t − 1 , a t − 1 ) , a t ∼ π θ ( a t ∣ s t ) [ ∑ t r ( s t , a t ) ] p ( τ ) = p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) π θ ( a t ∣ s t ) \begin{aligned} \theta^*&=\argmax_\theta E_{\tau\sim p_\theta(\tau)}\Big[r(\tau)\Big]\\ &=\argmax_\pi E_{s_t\sim p(s_t|s_{t-1},a_{t-1}),a_t\sim \pi_\theta(a_t|s_t)}\Big[\sum_tr(s_t,a_t)\Big]\\ p(\tau)&=p(s_1)\prod_{t=1}^T p(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t) \end{aligned} θ∗p(τ)=θargmaxEτ∼pθ(τ)[r(τ)]=πargmaxEst∼p(st∣st−1,at−1),at∼πθ(at∣st)[t∑r(st,at)]=p(s1)t=1∏Tp(st+1∣st,at)πθ(at∣st)
在dynamics环境 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)与我们的目标policy即 π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st)的共同作用下,产生一些trajectory即 τ \tau τ,根据最大化trajectory expected reward的目标约束下调整policy,使其最优
但是在Soft Framework里的出发点完全不一样,一没有Objective,二是从概率图角度构建问题的,因此对于一个带有optimal这种intent的trajectory的产生有:
p ( τ ∣ O 1 : T ) = p ( s 1 : T , a 1 : T ∣ O 1 : T ) ∝ p ( s 1 : T , a 1 : T , O 1 : T ) = p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) p ( O t ∣ s t , a t ) = [ p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] e x p ( ∑ t = 1 T r ( s t , a t ) ) \begin{aligned} p(\tau|O_{1:T})&=p(s_{1:T},a_{1:T}|O_{1:T})\\ &\propto p(s_{1:T},a_{1:T},O_{1:T})\\ &=p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)p(O_t|s_t,a_t)\\ &=\Big[p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)\Big]exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) \end{aligned} p(τ∣O1:T)=p(s1:T,a1:T∣O1:T)∝p(s1:T,a1:T,O1:T)=p(s1)t=1∏Tp(st+1∣st,at)p(Ot∣st,at)=[p(s1)t=1∏Tp(st+1∣st,at)]exp(t=1∑Tr(st,at))
通过归一化之类的方式,有
p ( τ ∣ O 1 : T ) = [ p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] ⏟ F e a s i b l e T r a j e c t o r y e x p ( ∑ t = 1 T r ( s t , a t ) ) p(\tau|O_{1:T})=\Big[\underbrace{p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)\Big]}_{Feasible\quad Trajectory}exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) p(τ∣O1:T)=[FeasibleTrajectory p(s1)t=1∏Tp(st+1∣st,at)]exp(t=1∑Tr(st,at))
最优轨迹的分布除了不可控的环境dynamics以外,就剩下由reward控制了。(如果有expert demonstration的话,实际上 p ( τ ∣ O 1 : T ) p(\tau|O_{1:T}) p(τ∣O1:T)就是专家数据的建模表示)
而实际上我们要的是一个policy即 p ( a t ∣ s t , O 1 : T ) p(a_t|s_t,O_{1:T}) p(at∣st,O1:T),于是希望通过Learning使policy产生的trajectory distribution与上述引入Optimal Variable的专家轨迹分布接近,即
p ^ ( τ ) = p ( s 1 ∣ O 1 : T ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t , O 1 : T ) p ( a t ∣ s t , O 1 : T ) \hat p(\tau)=p(s_1|O_{1:T})\prod_{t=1}^Tp(s_{t+1}|s_t,a_t,O_{1:T})p(a_t|s_t,O_{1:T}) p^(τ)=p(s1∣O1:T)t=1∏Tp(st+1∣st,at,O1:T)p(at∣st,O1:T)
2.3.3 Deterministic dynamics的Objective
在Deterministic dynamics的情况下,做一些简化
- 因为只有一个transition的状态,所以有 p ( s t + 1 ∣ s t , a t , O 1 : T ) = p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t,O_{1:T})=p(s_{t+1}|s_t,a_t) p(st+1∣st,at,O1:T)=p(st+1∣st,at)
- 初始状态可人为设定,不太重要即可令 p ( s 1 ∣ O 1 : T ) = p ( s 1 ) p(s_1|O_{1:T})=p(s_1) p(s1∣O1:T)=p(s1)
- 我们想学习的策略 π θ ( a t ∣ s t ) = p ( a t ∣ s t , O 1 : T ) \pi_\theta(a_t|s_t)=p(a_t|s_t,O_{1:T}) πθ(at∣st)=p(at∣st,O1:T)
所以目前有Soft Optimality概率图reward最优的轨迹分布:
p ( τ ∣ O 1 : T ) = [ p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] ⏟ F e a s i b l e T r a j e c t o r y e x p ( ∑ t = 1 T r ( s t , a t ) ) p(\tau|O_{1:T})=\Big[\underbrace{p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)\Big]}_{Feasible\quad Trajectory}exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) p(τ∣O1:T)=[FeasibleTrajectory p(s1)t=1∏Tp(st+1∣st,at)]exp(t=1∑Tr(st,at))
通过我们的目标policy构造的轨迹分布:
p ^ ( τ ∣ O 1 : T ) = p ( s 1 ∣ O 1 : T ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t , O 1 : T ) p ( a t ∣ s t , O 1 : T ) = p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) π θ ( a t ∣ s t ) \begin{aligned} \hat p(\tau|O_{1:T})&=p(s_1|O_{1:T})\prod_{t=1}^Tp(s_{t+1}|s_t,a_t,O_{1:T})p(a_t|s_t,O_{1:T})\\ &=p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t) \end{aligned} p^(τ∣O1:T)=p(s1∣O1:T)t=1∏Tp(st+1∣st,at,O1:T)p(at∣st,O1:T)=p(s1)t=1∏Tp(st+1∣st,at)πθ(at∣st)
我们拉近这两个分布
min θ D K L ( p ^ ( τ ∣ O 1 : T ) ∣ ∣ p ( τ ∣ O 1 : T ) ) = min θ E τ ∼ p ^ ( τ ) [ l o g p ^ ( τ ) − l o g p ( τ ) ] = max θ E τ ∼ p ^ ( τ ) [ l o g p ( τ ) − l o g p ^ ( τ ) ] = max θ E τ ∼ p ^ ( τ ) [ l o g p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) e x p ( ∑ t = 1 T r ( s t , a t ) ) − l o g p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] π θ ( a t ∣ s t ) ] = max θ E τ ∼ p ^ ( τ ) [ ∑ t = 1 T [ r ( s t , a t ) − l o g π θ ( a t ∣ s t ) ] ] = max θ ∑ t = 1 T E ( s t , a t ) ∼ p ^ ( s t , a t ) [ r ( s t , a t ) ] + ∑ t = 1 T E s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) [ − l o g π θ ( a t ∣ s t ) ] = max θ ∑ t = 1 T E ( s t , a t ) ∼ p ^ ( s t , a t ) [ r ( s t , a t ) ] + E s t ∼ p ^ ( s t ) [ H [ π θ ( a t ∣ s t ) ] ] \begin{aligned} \min_\theta D_{KL}\Big(\hat p(\tau|O_{1:T})||p(\tau|O_{1:T})\Big)&=\min_\theta E_{\tau\sim\hat p(\tau)}\Big[log\hat p(\tau)-logp(\tau)\Big]\\ &=\max_\theta E_{\tau\sim\hat p(\tau)}\Big[logp(\tau)-log\hat p(\tau)\Big]\\ &=\max_\theta E_{\tau\sim\hat p(\tau)}\Big[logp(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big)-logp(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)]\pi_\theta(a_t|s_t)\Big]\\ &=\max_\theta E_{\tau\sim\hat p(\tau)}\Big[\sum_{t=1}^T[r(s_t,a_t)-log\pi_\theta(a_t|s_t)]\Big]\\ &=\max_\theta \sum_{t=1}^TE_{(s_t,a_t)\sim\hat p(s_t,a_t)}\Big[r(s_t,a_t)\Big]+\sum_{t=1}^TE_{s_t\sim\hat p(s_t),a_t\sim \pi_\theta(a_t|s_t)}\Big[-log\pi_\theta(a_t|s_t)\Big]\\ &=\max_\theta \sum_{t=1}^TE_{(s_t,a_t)\sim\hat p(s_t,a_t)}\Big[r(s_t,a_t)\Big]+E_{s_t\sim\hat p(s_t)}\Big[H[\pi_\theta(a_t|s_t)]\Big]\\ \end{aligned} θminDKL(p^(τ∣O1:T)∣∣p(τ∣O1:T))=θminEτ∼p^(τ)[logp^(τ)−logp(τ)]=θmaxEτ∼p^(τ)[logp(τ)−logp^(τ)]=θmaxEτ∼p^(τ)[logp(s1)t=1∏Tp(st+1∣st,at)exp(t=1∑Tr(st,at))−logp(s1)t=1∏Tp(st+1∣st,at)]πθ(at∣st)]=θmaxEτ∼p^(τ)[t=1∑T[r(st,at)−logπθ(at∣st)]]=θmaxt=1∑TE(st,at)∼p^(st,at)[r(st,at)]+t=1∑TEst∼p^(st),at∼πθ(at∣st)[−logπθ(at∣st)]=θmaxt=1∑TE(st,at)∼p^(st,at)[r(st,at)]+Est∼p^(st)[H[πθ(at∣st)]]
于是发现通过概率图对stochastic optimal behavior 建模后,在deterministic dynamics的情况下,希望我们想要的policy与专家数据中的policy接近 m i n D K L minD_{KL} minDKL,其相当于优化目标Maximum Entropy Objective!
2.3.4 Stochastic Dynamics的Objective
当环境是Stochastic的情况下,
p ^ ( τ ∣ O 1 : T ) = p ( s 1 ∣ O 1 : T ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t , O 1 : T ) p ( a t ∣ s t , O 1 : T ) \hat p(\tau|O_{1:T})=p(s_1|O_{1:T})\prod_{t=1}^Tp(s_{t+1}|s_t,a_t,O_{1:T})p(a_t|s_t,O_{1:T}) p^(τ∣O1:T)=p(s1∣O1:T)t=1∏Tp(st+1∣st,at,O1:T)p(at∣st,O1:T)
p ( s t + 1 ∣ s t , a t , O 1 : T ) ≠ p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t,O_{1:T})\neq p(s_{t+1}|s_t,a_t) p(st+1∣st,at,O1:T)=p(st+1∣st,at),因为不只有一个transition状态了,但初始化状态还是可以设成一样的即 p ( s 1 ∣ O 1 : T ) = p ( s 1 ) p(s_1|O_{1:T})=p(s_1) p(s1∣O1:T)=p(s1)。这说明,在Soft Optimality Framework的情况下,Stochastic的时候Agent具备操纵dynamics的能力,我们想Agent只能操纵Policy才对,那怎么办呢?
Variational Inference进行分布近似
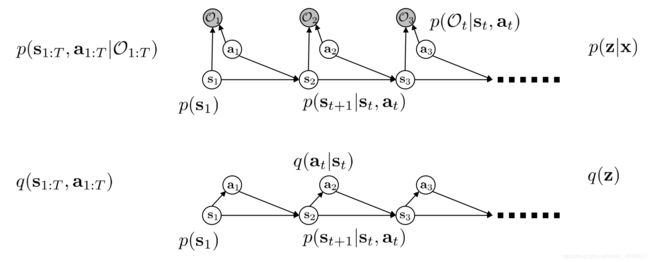
构建一个新的轨迹分布 q ( τ ) = q ( s 1 : T , a 1 : T ) q(\tau)=q(s_{1:T},a_{1:T}) q(τ)=q(s1:T,a1:T)来近似 p ^ ( τ ) = p ( s 1 : T , a 1 : T ∣ O 1 : T ) \hat p(\tau)=p(s_{1:T},a_{1:T}|O_{1:T}) p^(τ)=p(s1:T,a1:T∣O1:T),这个过程就如基础知识中提到的变分推断过程。
令 x = O 1 : T , z = ( s 1 : T , a 1 : T ) , q ( z ) = q ( τ ) = p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) q ( a t ∣ s t ) x=O_{1:T},z=(s_{1:T},a_{1:T}),q(z)=q(\tau)=p(s_1)\prod_tp(s_{t+1}|s_t,a_t)q(a_t|s_t) x=O1:T,z=(s1:T,a1:T),q(z)=q(τ)=p(s1)∏tp(st+1∣st,at)q(at∣st),由Variational Inference有:
l o g p ( O 1 : T ) = l o g p ( x ) ≥ E z ∼ q ( z ) [ l o g p ( x , z ) − l o g q ( z ) ] = E ( s 1 : T , a 1 : T ) ∼ q ( s 1 : T , a 1 : T ) [ l o g p ( s 1 : T , a 1 : T , O 1 : T ) − l o g q ( s 1 : T , a 1 : T ) ] = E ( s 1 : T , a 1 : T ) ∼ q ( s 1 : T , a 1 : T ) [ l o g p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) p ( O t ∣ s t , a t ) − l o g p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) q ( a t ∣ s t ) ] = E ( s 1 : T , a 1 : T ) ∼ q ( s 1 : T , a 1 : T ) [ ∑ t r ( s t , a t ) − l o g q ( a t ∣ s t ) ] = ∑ t E ( s t , a t ) ∼ q ( s t , a t ) [ r ( s t , a t ) ] + E s t ∼ q ( s t ) [ H [ q ( a t ∣ s t ) ] ] \begin{aligned} logp(O_{1:T})=logp(x)&\geq E_{z\sim q(z)}\Big[logp(x,z)-logq(z)\Big]\\ &=E_{(s_{1:T},a_{1:T}) \sim q(s_{1:T},a_{1:T})}\Big[logp(s_{1:T},a_{1:T},O_{1:T})-logq(s_{1:T},a_{1:T})\Big]\\ &=E_{(s_{1:T},a_{1:T}) \sim q(s_{1:T},a_{1:T})}\Big[logp(s_1)\prod_tp(s_{t+1}|s_t,a_t)p(O_t|s_t,a_t)-logp(s_1)\prod_tp(s_{t+1}|s_t,a_t)q(a_t|s_t)\Big]\\ &=E_{(s_{1:T},a_{1:T}) \sim q(s_{1:T},a_{1:T})}\Big[\sum_tr(s_t,a_t)-logq(a_t|s_t)\Big]\\ &=\sum_tE_{(s_{t},a_{t}) \sim q(s_{t},a_{t})}\Big[r(s_t,a_t)\Big]+E_{s_t\sim q(s_t)}\Big[H[q(a_t|s_t)]\Big]\\ \end{aligned} logp(O1:T)=logp(x)≥Ez∼q(z)[logp(x,z)−logq(z)]=E(s1:T,a1:T)∼q(s1:T,a1:T)[logp(s1:T,a1:T,O1:T)−logq(s1:T,a1:T)]=E(s1:T,a1:T)∼q(s1:T,a1:T)[logp(s1)t∏p(st+1∣st,at)p(Ot∣st,at)−logp(s1)t∏p(st+1∣st,at)q(at∣st)]=E(s1:T,a1:T)∼q(s1:T,a1:T)[t∑r(st,at)−logq(at∣st)]=t∑E(st,at)∼q(st,at)[r(st,at)]+Est∼q(st)[H[q(at∣st)]]
最大化这个ELBO,从末尾时刻T开始:
q ( a T ∣ s T ) = arg max E s T ∼ q ( s T ) [ E a T ∼ q ( a T ∣ s T ) [ r ( s T , a T ) ] + H ( q ( a T ∣ s T ) ) ] = arg max E s T ∼ q ( s T ) [ E a T ∼ q ( a T ∣ s T ) [ r ( s T , a T ) − log q ( a T ∣ s T ) ] ] \begin{aligned} q\left(\mathbf{a}_{T} | \mathbf{s}_{T}\right) &=\arg \max E_{\mathbf{s}_{T} \sim q\left(\mathbf{s}_{T}\right)}\left[E_{\mathbf{a}_{T} \sim q\left(\mathbf{a}_{T} | \mathbf{s}_{T}\right)}\left[r\left(\mathbf{s}_{T}, \mathbf{a}_{T}\right)\right]+\mathcal{H}\left(q\left(\mathbf{a}_{T} | \mathbf{s}_{T}\right)\right)\right] \\ &=\arg \max E_{\mathbf{s}_{T} \sim q\left(\mathbf{s}_{T}\right)}\left[E_{\mathbf{a}_{T} \sim q\left(\mathbf{a}_{T} | \mathbf{s}_{T}\right)}\left[r\left(\mathbf{s}_{T}, \mathbf{a}_{T}\right)-\log q\left(\mathbf{a}_{T} | \mathbf{s}_{T}\right)\right]\right] \end{aligned} q(aT∣sT)=argmaxEsT∼q(sT)[EaT∼q(aT∣sT)[r(sT,aT)]+H(q(aT∣sT))]=argmaxEsT∼q(sT)[EaT∼q(aT∣sT)[r(sT,aT)−logq(aT∣sT)]]
如何选择这个 a T a_T aT呢?末尾时刻T肯定跟着reward的大小选择呀!
q ( a T ∣ s T ) = e x p ( r ( s T , a T ) ) ∫ e x p ( r ( s T , a T ) ) d a = e x p ( Q ( s T , a T ) − V ( s T ) ) q(a_T|s_T)=\frac{exp(r(s_T,a_T))}{\int exp(r(s_T,a_T))da}=exp(Q(s_T,a_T)-V(s_T)) q(aT∣sT)=∫exp(r(sT,aT))daexp(r(sT,aT))=exp(Q(sT,aT)−V(sT))
最后时刻有 r ( s T , a T ) = Q ( s T , a T ) r(s_T,a_T)=Q(s_T,a_T) r(sT,aT)=Q(sT,aT),且
l o g q ( a T ∣ s T ) = Q ( s T , a T ) − V ( s T ) logq(a_T|s_T)=Q(s_T,a_T)-V(s_T) logq(aT∣sT)=Q(sT,aT)−V(sT)
所以:
q ( a T ∣ s T ) = E s T ∼ q ( s T ) [ E a T ∼ q ( a T ∣ s T ) [ V ( s T ) ] ] q(a_T|s_T)=E_{s_T\sim q(s_T)}\big[E_{a_T\sim q(a_T|s_T)}[V(s_T)]\big] q(aT∣sT)=EsT∼q(sT)[EaT∼q(aT∣sT)[V(sT)]]
我们解了个啥?选择policy即 q ( a t ∣ s t ) q(a_t|s_t) q(at∣st)来最大化ELBO:
l o g p ( O 1 : T ) ≥ ∑ t = 1 T E ( s t , a t ) ∼ q ( s t , a t ) [ r ( s t , a t ) ] + E s t ∼ q ( s t ) [ H [ q ( a t ∣ s t ) ] ] logp(O_{1:T})\geq\sum_{t=1}^TE_{(s_{t},a_{t}) \sim q(s_{t},a_{t})}\Big[r(s_t,a_t)\Big]+E_{s_t\sim q(s_t)}\Big[H[q(a_t|s_t)]\Big] logp(O1:T)≥t=1∑TE(st,at)∼q(st,at)[r(st,at)]+Est∼q(st)[H[q(at∣st)]]
选了末尾时刻T开始考虑,得出一项: q ( a T ∣ s T ) = E s T ∼ q ( s T ) [ E a T ∼ q ( a T ∣ s T ) [ V ( s T ) ] ] q(a_T|s_T)=E_{s_T\sim q(s_T)}\big[E_{a_T\sim q(a_T|s_T)}[V(s_T)]\big] q(aT∣sT)=EsT∼q(sT)[EaT∼q(aT∣sT)[V(sT)]]
于是普通的情况 q ( a t ∣ s t ) q(a_t|s_t) q(at∣st)有:
q ( a t ∣ s t ) = arg max E s t ∼ q ( s t ) [ E a t ∼ q ( a t ∣ s t ) [ r ( s t , a t ) + E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V ( s t + 1 ) ] ] + H ( q ( a t ∣ s t ) ) ] = arg max E s t ∼ q ( s t ) [ E a t ∼ q ( a t ∣ s t ) [ Q ( s t , a t ) ] + H ( q ( a t ∣ s t ) ) ] = arg max E s t ∼ q ( s t ) [ E a t ∼ q ( a t ∣ s t ) [ Q ( s t , a t ) − log q ( a t ∣ s t ) ] ] \begin{aligned} q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right) &=\arg \max E_{\mathbf{s}_{t} \sim q\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)}\left[r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+E_{\mathbf{s}_{t+1} \sim p\left(\mathbf{s}_{t+1} | \mathbf{s}_{t}, \mathbf{a}_{t}\right)}\left[V\left(\mathbf{s}_{t+1}\right)\right]\right]+\mathcal{H}\left(q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)\right)\right] \\ &=\arg \max E_{\mathbf{s}_{t} \sim q\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]+\mathcal{H}\left(q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)\right)\right] \\ &=\arg \max E_{\mathbf{s}_{t} \sim q\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\log q\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)\right]\right] \end{aligned} q(at∣st)=argmaxEst∼q(st)[Eat∼q(at∣st)[r(st,at)+Est+1∼p(st+1∣st,at)[V(st+1)]]+H(q(at∣st))]=argmaxEst∼q(st)[Eat∼q(at∣st)[Q(st,at)]+H(q(at∣st))]=argmaxEst∼q(st)[Eat∼q(at∣st)[Q(st,at)−logq(at∣st)]]
最终有,
Q t ( s t , a t ) = r ( s t , a t ) + E [ V t + 1 ( s t + 1 ) ] V t ( s t ) = l o g ∫ e x p ( Q t ( s t , a t ) ) d a t q ( a t ∣ s t ) = e x p ( Q ( s t , a t ) − V ( s t ) ) Q_t(s_t,a_t)=r(s_t,a_t)+E[V_{t+1}(s_{t+1})]\\ V_t(s_t)=log\int exp(Q_t(s_t,a_t))da_t\\ q(a_t|s_t)=exp(Q(s_t,a_t)-V(s_t)) Qt(st,at)=r(st,at)+E[Vt+1(st+1)]Vt(st)=log∫exp(Qt(st,at))datq(at∣st)=exp(Q(st,at)−V(st))
2.4 Soft Value Iteration
经过Soft Optimality在Deterministic与Stochastic的dynamics下,才知道原来我们在优化的Objective不过是加了个Entropy term,因为PGM建模方式有个Optimism Problem的问题,于是通过Variational Inference解决Stochastic Dynamics后终于发现了与Value Iteration关键的联系!!!
为大家呈现Soft Value Iteration:

它们之间的对比:

2.5 Soft Q-leanring
知道了Softmax的含义后,即
s o f t m a x a Q ( s , a ) = l o g ∫ e x p ( V ( s ) ) d a softmax_aQ(s,a)=log\int exp(V(s))da softmaxaQ(s,a)=log∫exp(V(s))da
将原来的Q-learning中Q值换一个Softemax就变成Soft Q-leanring了!

只需要注意一下policy的获取 π ( a ∣ s ) = e x p ( Q ( s , a ) − V ( s ) ) = e x p ( A ( s , a ) ) \pi(a|s)=exp(Q(s,a)-V(s))=exp(A(s,a)) π(a∣s)=exp(Q(s,a)−V(s))=exp(A(s,a)),因为只有这种形式的policy才能Optimize刚才辛苦推断出来的Objective,具体的参数更新为:
ϕ ← ϕ + α ∇ ϕ Q ϕ ( s , a ) ( r ( s , a ) + γ V ( s ′ ) − Q ϕ ( s , a ) ) V ( s ′ ) = l o g ∫ exp ( Q ϕ ( s ′ , a ′ ) ) d a ′ \phi\leftarrow\phi+\alpha\nabla_\phi Q_\phi(s,a)\Big(r(s,a)+\gamma V(s')-Q_\phi(s,a)\Big)\\ V(s')=log\int\exp(Q_\phi(s',a'))da' ϕ←ϕ+α∇ϕQϕ(s,a)(r(s,a)+γV(s′)−Qϕ(s,a))V(s′)=log∫exp(Qϕ(s′,a′))da′
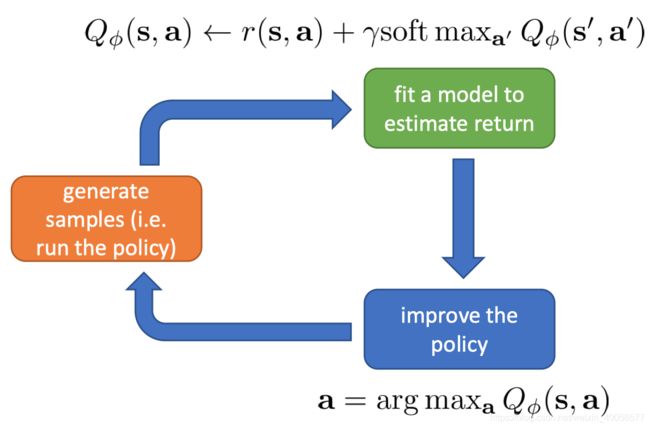
于是Q-learning所有tricks都可以往上蹭了,如Double Q-Network、Dueling Structure、HER等等,具体可以参见Rainbow AAAI 2018这篇集齐所有tricks的Paper~
2.6 Policy Gradient with Soft Optimality
我们从上面,推断出Soft Optimality的Objective:
min θ J ( θ ) = min θ D K L ( p ^ ( τ ) ∣ ∣ p ( τ ) ) = max θ ∑ t = 1 T E ( s t , a t ) ∼ p ^ ( s t , a t ) [ r ( s t , a t ) ] + E s t ∼ p ^ ( s t ) [ H [ π θ ( a t ∣ s t ) ] ] = max θ ∑ t = 1 T E ( s t , a t ) ∼ p ^ ( s t , a t ) [ r ( s t , a t ) − l o g π θ ( a t ∣ s t ) ] = max θ ∑ t = 1 T E s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) [ r ( s t , a t ) − l o g π θ ( a t ∣ s t ) ] \begin{aligned} \min_\theta J(\theta)&=\min_\theta D_{KL}\Big(\hat p(\tau)||p(\tau)\Big)\\ &=\max_\theta \sum_{t=1}^TE_{(s_t,a_t)\sim\hat p(s_t,a_t)}\Big[r(s_t,a_t)\Big]+E_{s_t\sim\hat p(s_t)}\Big[H[\pi_\theta(a_t|s_t)]\Big]\\ &=\max_\theta \sum_{t=1}^TE_{(s_t,a_t)\sim\hat p(s_t,a_t)}\Big[r(s_t,a_t)-log\pi_\theta(a_t|s_t)\Big]\\ &=\max_\theta \sum_{t=1}^TE_{s_t\sim \hat p(s_t),a_t\sim \pi_\theta(a_t|s_t)}\Big[r(s_t,a_t)-log\pi_\theta(a_t|s_t)\Big]\\ \end{aligned} θminJ(θ)=θminDKL(p^(τ)∣∣p(τ))=θmaxt=1∑TE(st,at)∼p^(st,at)[r(st,at)]+Est∼p^(st)[H[πθ(at∣st)]]=θmaxt=1∑TE(st,at)∼p^(st,at)[r(st,at)−logπθ(at∣st)]=θmaxt=1∑TEst∼p^(st),at∼πθ(at∣st)[r(st,at)−logπθ(at∣st)]
求梯度: ∇ J ( θ ) = ∇ θ ∑ t = 1 T E ( s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) ) [ r ( s t , a t ) ] + ∇ θ ∑ t = 1 T E ( s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) ) [ − l o g π θ ( a t ∣ s t ) ] \nabla J(\theta)=\nabla_\theta \sum_{t=1}^TE_{(s_t\sim \hat p(s_t),a_t\sim \pi_\theta(a_t|s_t)})\Big[r(s_t,a_t)\Big]+\nabla_\theta\sum_{t=1}^TE_{(s_t\sim \hat p(s_t),a_t\sim \pi_\theta(a_t|s_t)})\Big[-log\pi_\theta(a_t|s_t)\Big] ∇J(θ)=∇θt=1∑TE(st∼p^(st),at∼πθ(at∣st))[r(st,at)]+∇θt=1∑TE(st∼p^(st),at∼πθ(at∣st))[−logπθ(at∣st)]
第一项非常熟悉,先求:
∇ θ ∑ t = 1 T E s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) [ r ( s t , a t ) ] = ∇ θ E τ ∼ π θ ( τ ) [ r ( τ ) ] = ∇ θ ∫ π θ ( τ ) r ( τ ) d τ = ∫ π θ ( τ ) ∇ θ l o g π θ ( τ ) r ( τ ) d τ = E τ ∼ π θ ( τ ) [ ∇ θ l o g π θ ( τ ) r ( τ ) ] ( 1 ) = E ( s t , a t ) ∼ p ^ ( s t , a t ) [ ∑ t = 1 T ∇ θ l o g π ( a t ∣ s t ) ] [ ∑ t = 1 T r ( s t , a t ) ] → b a s e l i n e E ( s t , a t ) ∼ p ^ ( s t , a t ) [ ∑ t = 1 T ∇ θ l o g π ( a t ∣ s t ) ] [ ∑ t ′ = t T r ( s t ′ , a t ′ ) ] \begin{aligned} &\nabla_\theta \sum_{t=1}^TE_{s_t\sim \hat p(s_t),a_t\sim \pi_\theta(a_t|s_t)}\Big[r(s_t,a_t)\Big]\\ &=\nabla_\theta E_{\tau\sim\pi_\theta(\tau)}\Big[r(\tau)\Big]\\ &=\nabla_\theta \int \pi_\theta(\tau)r(\tau)d\tau\\ &=\int \pi_\theta(\tau)\nabla_\theta log\pi_\theta(\tau)r(\tau)d\tau\\ &=E_{\tau\sim \pi_\theta(\tau)}\Big[\nabla_\theta log\pi_\theta(\tau) r(\tau)\Big]\quad (1)\\ &=E_{(s_t,a_t)\sim \hat p(s_t,a_t)}\Big[\sum_{t=1}^T\nabla_\theta log\pi(a_t|s_t)\Big]\Big[\sum_{t=1}^Tr(s_t,a_t)\Big]\\ &\rightarrow^{baseline} E_{(s_t,a_t)\sim \hat p(s_t,a_t)}\Big[\sum_{t=1}^T\nabla_\theta log\pi(a_t|s_t)\Big]\Big[\sum_{t'=t}^Tr(s_{t'},a_{t'})\Big] \end{aligned} ∇θt=1∑TEst∼p^(st),at∼πθ(at∣st)[r(st,at)]=∇θEτ∼πθ(τ)[r(τ)]=∇θ∫πθ(τ)r(τ)dτ=∫πθ(τ)∇θlogπθ(τ)r(τ)dτ=Eτ∼πθ(τ)[∇θlogπθ(τ)r(τ)](1)=E(st,at)∼p^(st,at)[t=1∑T∇θlogπ(at∣st)][t=1∑Tr(st,at)]→baselineE(st,at)∼p^(st,at)[t=1∑T∇θlogπ(at∣st)][t′=t∑Tr(st′,at′)]
再求第二项,省略负号,后续加上:
∇ θ ∑ t = 1 T E s t ∼ p ^ ( s t ) , a t ∼ π θ ( a t ∣ s t ) [ l o g π θ ( a t ∣ s t ) ] = ∇ θ E τ ∼ π θ ( τ ) [ ∑ t = 1 T l o g π θ ( a t ∣ s t
