python数学建模之用optimize.linear_sum_assignment解决模型优化之指派问题
指派问题是那些派完成任务效率最高的人去完成任务的问题。在生活中经常遇到这样的问题,某单位需完成n项任务,恰好有n个人可承担这些任务。由于每人的专长不同,各人完成任务不同(或所费时间),效率也不同。于是产生应指派哪个人去完成哪项任务,使完成n项任务的总效率最高(或所需总时间最小)。这类问题称为指派问题或分派问题。
假设其指派矩阵如上所示,其意思是说列项表示人数,行项表示每人完成某项任务的时间或者效率,目标函数即为求取给每人安排一项任务,使所有人完成任务的时间最短或者效率最高。
如3表示第1个人完成任务a的时间或者效率,8表示第1个人完成b任务的时间或者效率。
python可以使用scipy.optimize.linear_sum_assignment函数解决该类问题。
文档连接:
说明文档![]() https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linear_sum_assignment.html?highlight=linear_sum_assignment#scipy.optimize.linear_sum_assignment
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linear_sum_assignment.html?highlight=linear_sum_assignment#scipy.optimize.linear_sum_assignment
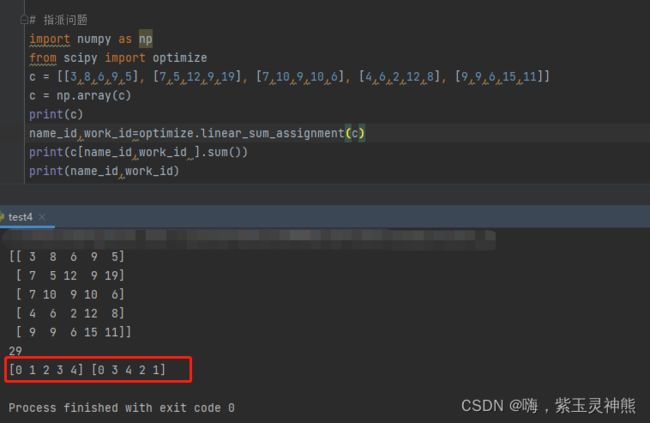
import numpy as np
from scipy import optimize
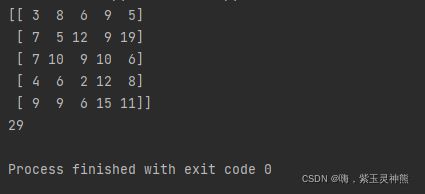
c = [[3,8,6,9,5], [7,5,12,9,19], [7,10,9,10,6], [4,6,2,12,8], [9,9,6,15,11]]
c = np.array(c)
print(c)
name_id,work_id=optimize.linear_sum_assignment(c)
print(c[name_id,work_id ].sum())结果如下:
也可以单独查看name_id ,与work_id,这两个变量记录的是人与其对应的工作分配:
对于第一个人分配的是a任务,第二个人分配的是d任务,第三个人分配的是e任务,第四个人分配的是c任务,第五个人分配的是b任务,这样的用时最短,或者效率最高。
对于人数少任务多的指派:如5个人指派7个任务
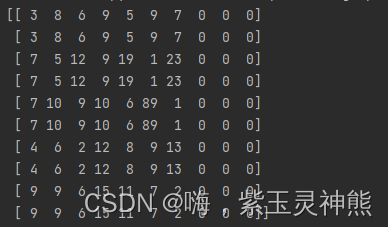
做法是将人数进行分身,即每个人分为2个人,添加3个虚拟任务,这样就构成一个10x10的矩阵,如下:
将最后三行都填0的意思是任何人去做这三个任务效率都很高,都可以分配给任何人。
运用上面的算法,结果如下:
import numpy as np
from scipy import optimize
c = [[3,8,6,9,5,9,7,0,0,0], [3,8,6,9,5,9,7,0,0,0],[7,5,12,9,19,1,23,0,0,0],[7,5,12,9,19,1,23,0,0,0],
[7,10,9,10,6,89,1,0,0,0],[7,10,9,10,6,89,1,0,0,0],
[4,6,2,12,8,9,13,0,0,0],[4,6,2,12,8,9,13,0,0,0], [9,9,6,15,11,7,2,0,0,0], [9,9,6,15,11,7,2,0,0,0]]
c = np.array(c)
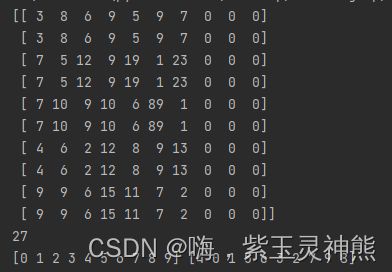
print(c)
name_id,work_id=optimize.linear_sum_assignment(c)
print(c[name_id,work_id ].sum())
print(name_id,work_id)算出来的最短时间为27,且分配如下:
第1个人分配任务0和4,第2个人分配任务1和5,第3个人分配任务6和3,第4个人分配任务2,第5个人不分配任务