PyTorch 源码解读之 BN & SyncBN：BN 与 多卡同步 BN 详解

目录

1. BatchNorm 原理

2. BatchNorm 的 PyTorch 实现

2.1 _NormBase 类

2.1.1 初始化

2.1.2 模拟 BN forward

2.1.3 running_mean、running_var 的更新

2.1.4 \gamma, \beta 的更新

2.1.5 eval 模式

2.2 BatchNormNd 类

3. SyncBatchNorm 的 PyTorch 实现

3.1 forward

3.2 backward

1. BatchNorm 原理

BatchNorm 最早在全连接网络中被提出，对每个神经元的输入做归一化。扩展到 CNN 中，就是对每个卷积核的输入做归一化，或者说在 channel 之外的所有维度做归一化。 BN 带来的好处有很多，这里简单列举几个：

• 防止过拟合：单个样本的输出依赖于整个 mini-batch，防止对某个样本过拟合；
• 加快收敛：梯度下降过程中，每一层的  和  都会不断变化，导致输出结果的分布在不断变化，后层网络就要不停地去适应这种分布变化。用 BN 后，可以使每一层输入的分布近似不变。
• 防止梯度弥散：forward 过程中，逐渐往非线性函数的取值区间的上下限两端靠近，（以 Sigmoid 为例），此时后面层的梯度变得非常小，不利于训练。

BN 的数学表达为： 

这里引入了缩放因子  和平移因子  ，作者在文章里解释了它们的作用：

• Normalize 到 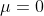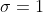， ,  会导致新的分布丧失从前层传递过来的特征与知识
• 以 Sigmoid 为例，加入 ， ,  可以防止大部分值落在近似线性的中间部分，导致无法利用非线性的部分

2. BatchNorm 的 PyTorch 实现

PyTorch 中与 BN 相关的几个类放在 torch.nn.modules.batchnorm 中，包含以下几个类：

• _NormBase：nn.Module 的子类，定义了 BN 中的一系列属性与初始化、读数据的方法；
• _BatchNorm：_NormBase 的子类，定义了 forward 方法；
• BatchNorm1d & BatchNorm2d & BatchNorm3d：_BatchNorm的子类，定义了不同的_check_input_dim方法。

2.1 _NormBase 类

2.1.1 初始化

_NormBase类定义了 BN 相关的一些属性，如下表所示：

attribute	meaning
num_features	输入的 channel 数
track_running_stats	默认为 True，是否统计 running_mean，running_var
running_mean	训练时统计输入的 mean，之后用于 inference
running_var	训练时统计输入的 var，之后用于 inference
momentum	默认 0.1，更新 running_mean，running_var 时的动量
num_batches_tracked	PyTorch 0.4 后新加入，当 momentum 设置为 None 时，使用 num_batches_tracked 计算每一轮更新的动量
affine	默认为 True，训练 weight 和 bias；否则不更新它们的值
weight	公式中的 \gamma，初始化为全 1 tensor
bias	公式中的 \beta，初始化为全 0 tensor

这里贴一下 PyTorch 的源码：

class _NormBase(Module):
    """Common base of _InstanceNorm and _BatchNorm"""
    # 读checkpoint时会用version来区分是 PyTorch 0.4.1 之前还是之后的版本
    _version = 2
    __constants__ = ['track_running_stats', 'momentum', 'eps',
                     'num_features', 'affine']

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
        super(_NormBase, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.affine = affine
        self.track_running_stats = track_running_stats
        if self.affine:
            # 如果打开 affine，就使用缩放因子和平移因子
            self.weight = Parameter(torch.Tensor(num_features))
            self.bias = Parameter(torch.Tensor(num_features))
        else:
            self.register_parameter('weight', None)
            self.register_parameter('bias', None)
        # 训练时是否需要统计 mean 和 variance
        if self.track_running_stats:
            # buffer 不会在self.parameters()中出现
            self.register_buffer('running_mean', torch.zeros(num_features))
            self.register_buffer('running_var', torch.ones(num_features))
            self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
        else:
            self.register_parameter('running_mean', None)
            self.register_parameter('running_var', None)
            self.register_parameter('num_batches_tracked', None)
        self.reset_parameters()

    def reset_running_stats(self):
        if self.track_running_stats:
            self.running_mean.zero_()
            self.running_var.fill_(1)
            self.num_batches_tracked.zero_()

    def reset_parameters(self):
        self.reset_running_stats()
        if self.affine:
            init.ones_(self.weight)
            init.zeros_(self.bias)

    def _check_input_dim(self, input):
        # 具体在 BN1d, BN2d, BN3d 中实现，验证输入合法性
        raise NotImplementedError

    def extra_repr(self):
        return '{num_features}, eps={eps}, momentum={momentum}, affine={affine}, ' \
               'track_running_stats={track_running_stats}'.format(**self.__dict__)

    def _load_from_state_dict(self, state_dict, prefix, local_metadata, strict,
                              missing_keys, unexpected_keys, error_msgs):
        version = local_metadata.get('version', None)

        if (version is None or version < 2) and self.track_running_stats:
            # at version 2: added num_batches_tracked buffer
            #               this should have a default value of 0
            num_batches_tracked_key = prefix + 'num_batches_tracked'
            if num_batches_tracked_key not in state_dict:
                # 旧版本的checkpoint没有这个key，设置为0
                state_dict[num_batches_tracked_key] = torch.tensor(0, dtype=torch.long)

        super(_NormBase, self)._load_from_state_dict(
            state_dict, prefix, local_metadata, strict,
            missing_keys, unexpected_keys, error_msgs)


class _BatchNorm(_NormBase):

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
        super(_BatchNorm, self).__init__(
            num_features, eps, momentum, affine, track_running_stats)

    def forward(self, input):
        self._check_input_dim(input)

        # exponential_average_factor is set to self.momentum
        # (when it is available) only so that it gets updated
        # in ONNX graph when this node is exported to ONNX.
        if self.momentum is None:
            exponential_average_factor = 0.0
        else:
            exponential_average_factor = self.momentum

        # 如果在train状态且self.track_running_stats被设置为True，就需要更新统计量
        if self.training and self.track_running_stats:
            if self.num_batches_tracked is not None:
                self.num_batches_tracked = self.num_batches_tracked + 1
                # 如果momentum被设置为None，就用num_batches_tracked来加权
                if self.momentum is None:
                    exponential_average_factor = 1.0 / float(self.num_batches_tracked)
                else:  # use exponential moving average
                    exponential_average_factor = self.momentum

        return F.batch_norm(
            input, self.running_mean, self.running_var, self.weight, self.bias,
            self.training or not self.track_running_stats,
            exponential_average_factor, self.eps)

2.1.2 模拟 BN forward

PyTorch 中 BN 的 Python 部分代码主要实现初始化、传参和底层方法调用。这里用 Python 模拟 BN 的底层计算。

import torch
import torch.nn as nn
import torch.nn.modules.batchnorm

# 创建随机输入
def create_inputs():
    return torch.randn(8, 3, 20, 20)

# 以 BatchNorm2d 为例
# mean_val, var_val 不为None时，不对输入进行统计，而直接用传进来的均值、方差
def dummy_bn_forward(x, bn_weight, bn_bias, eps, mean_val=None, var_val=None):
    if mean_val is None:
        mean_val = x.mean([0, 2, 3])
    if var_val is None:
        # 这里需要注意，torch.var 默认算无偏估计，因此需要手动设置unbiased=False
        var_val = x.var([0, 2, 3], unbiased=False)

    x = x - mean_val[None, ..., None, None]
    x = x / torch.sqrt(var_val[None, ..., None, None] + eps)
    x = x * bn_weight[..., None, None] + bn_bias[..., None, None]
    return mean_val, var_val, x

验证 dummy BN 输出的正确性：

bn_layer = nn.BatchNorm2d(num_features=3)
inputs = create_inputs()
# 用 pytorch 的实现 forward 
bn_outputs = bn_layer(inputs)
# 用 dummy bn 来 forward
_, _, expected_outputs = dummy_bn_forward(
    inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps)
assert torch.allclose(expected_outputs, bn_outputs)

没有报异常，因此计算的值是正确的。

2.1.3 running_mean、running_var 的更新

BatchNorm 默认打开 track_running_stats，因此每次 forward 时都会依据当前 minibatch 的统计量来更新 running_mean 和 running_var。

momentum 默认值为 0.1，控制历史统计量与当前 minibatch 在更新 running_mean、running_var 时的相对影响。

running_mean = running_mean * (1 - momentum) + E[x] * momentum,

running_var= running_var * (1 - momentum) + Var[x] * momentum, 

其中  、 分别表示  的均值、方差；需要注意这里统计方差时用了无偏估计，与论文保持一致。手动对这一过程进行模拟，如下所示：

running_mean = torch.zeros(3)
running_var = torch.ones_like(running_mean)
momentum = 0.1 # 这也是BN初始化时momentum默认值
bn_layer = nn.BatchNorm2d(num_features=3, momentum=momentum)

# 模拟 forward 10 次
for t in range(10):
    inputs = create_inputs()
    bn_outputs = bn_layer(inputs)
    inputs_mean, inputs_var, _ = dummy_bn_forward(
        inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps
    )
    n = inputs.numel() / inputs.size(1)
    # 更新 running_var 和 running_mean
    running_var = running_var * (1 - momentum) + momentum * inputs_var * n / (n - 1)
    running_mean = running_mean * (1 - momentum) + momentum * inputs_mean

assert torch.allclose(running_var, bn_layer.running_var)
assert torch.allclose(running_mean, bn_layer.running_mean)
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'dummy bn running_mean is {running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
print(f'dummy bn running_var is {running_var}')

输出结果：

bn_layer running_mean is tensor([ 0.0101, -0.0013, 0.0101])
dummy bn running_mean is tensor([ 0.0101, -0.0013, 0.0101])
bn_layer running_var is tensor([0.9857, 0.9883, 1.0205])
dummy bn running_var is tensor([0.9857, 0.9883, 1.0205])

running_mean 的初始值为 0，forward 后发生变化。同时模拟 BN 的running_mean,running_var 也与 PyTorch 实现的结果一致。

以上讨论的是使用momentum的情况。在 PyTorch 0.4.1 后，加入了num_batches_tracked属性，统计 BN 一共 forward 了多少个 minibatch。当momentum被设置为None时，就由num_batches_tracked来控制历史统计量与当前 minibatch 的影响占比：

q = 1.0/num_batches_tracked,

running_mean= running_mean * (1 - q) + E[x] * q, 

running_var = running_var * (1 - q) + Var[x] * q. 

接下来手动模拟这一过程：

running_mean = torch.zeros(3)
running_var = torch.ones_like(running_mean)
num_batches_tracked = 0
# momentum 设置成 None，用 num_batches_tracked 来更新统计量
bn_layer = nn.BatchNorm2d(num_features=3, momentum=None)

# 同样是模拟 forward 10次
for t in range(10):
    inputs = create_inputs()
    bn_outputs = bn_layer(inputs)
    inputs_mean, inputs_var, _ = dummy_bn_forward(
        inputs, bn_layer.weight, bn_layer.bias, bn_layer.eps
    )
    num_batches_tracked += 1
    # exponential_average_factor
    eaf = 1.0 / num_batches_tracked
    n = inputs.numel() / inputs.size(1)
    # 更新 running_var 和 running_mean
    running_var = running_var * (1 - eaf) + eaf * inputs_var * n / (n - 1)
    running_mean = running_mean * (1 - eaf) + eaf * inputs_mean

assert torch.allclose(running_var, bn_layer.running_var)
assert torch.allclose(running_mean, bn_layer.running_mean)

bn_layer.train(mode=False)
inference_inputs = create_inputs()
bn_outputs = bn_layer(inference_inputs)
_, _, dummy_outputs = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps,
    running_mean, running_var)
assert torch.allclose(dummy_outputs, bn_outputs)
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'dummy bn running_mean is {running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
print(f'dummy bn running_var is {running_var}')

输出：

bn_layer running_mean is tensor([-0.0040, 0.0074, -0.0162])
dummy bn running_mean is tensor([-0.0040, 0.0074, -0.0162])
bn_layer running_var is tensor([1.0097, 1.0086, 0.9815])
dummy bn running_var is tensor([1.0097, 1.0086, 0.9815])

手动模拟的结果与 PyTorch 相同。

2.1.4  ,  的更新

BatchNorm 的 weight，bias 分别对应公式里的  ,  , 更新方式是梯度下降法。

import torchvision
from torchvision.transforms import Normalize, ToTensor, Compose
import torch.nn.functional as F
from torch.utils.data.dataloader import DataLoader

# 用 mnist 作为 toy dataset
mnist = torchvision.datasets.MNIST(root='mnist', download=True, transform=ToTensor())
dataloader = DataLoader(dataset=mnist, batch_size=8)

# 初始化一个带 BN 的简单模型
toy_model = nn.Sequential(nn.Linear(28 ** 2, 128), nn.BatchNorm1d(128),
                          nn.ReLU(), nn.Linear(128, 10), nn.Sigmoid())
optimizer = torch.optim.SGD(toy_model.parameters(), lr=0.1)

bn_1d_layer = toy_model[1]
print(f'Initial weight is {bn_layer.weight[:4].tolist()}...')
print(f'Initial bias is {bn_layer.bias[:4].tolist()}...\n')
# 模拟更新2次参数
for (i, data) in enumerate(dataloader):
    output = toy_model(data[0].view(data[0].shape[0], -1))
    (F.cross_entropy(output, data[1])).backward()
    # 输出部分参数的梯度，验证weight和bias确实是通过gradient descent更新的
    print(f'Gradient of weight is {bn_1d_layer.weight.grad[:4].tolist()}...')
    print(f'Gradient of bias is {bn_1d_layer.bias.grad[:4].tolist()}...')
    optimizer.step()
    optimizer.zero_grad()
    if i == 1:
        break
print(f'\nNow weight is {bn_1d_layer.weight[:4].tolist()}...')
print(f'Now bias is {bn_1d_layer.bias[:4].tolist()}...')

inputs = torch.randn(4, 128)
bn_outputs = bn_1d_layer(inputs)
new_bn = nn.BatchNorm1d(128)
bn_outputs_no_weight_bias = new_bn(inputs)

assert not torch.allclose(bn_outputs, bn_outputs_no_weight_bias)

输出：

Initial weight is [0.9999354481697083, 1.0033478736877441, 1.0019147396087646, 0.9986106157302856]...
Initial bias is [-0.0012734815245494246, 0.001349383033812046, 0.0013358002761378884, -0.0007148777367547154]...

Gradient of weight is [-0.0004475426103454083, -0.0021388232707977295, -0.0032624618615955114, -0.0009599098702892661]...
Gradient of bias is [0.00011698803427862003, -0.001291472464799881, -0.0023048489820212126, -0.0009493136312812567]...
Gradient of weight is [-0.00035325769567862153, -0.0014295700239017606, -0.002102235099300742, 0.000851186050567776]...
Gradient of bias is [-0.00026844028616324067, -0.00025666248984634876, -0.0017800561618059874, 0.00024933076929301023]...

Now weight is [1.0000154972076416, 1.0037046670913696, 1.0024511814117432, 0.9986214637756348]...
Now bias is [-0.0012583363568410277, 0.0015041964361444116, 0.0017442908138036728, -0.0006448794738389552]...

2.1.5 eval 模式

上面验证的都是 train 模式下 BN 的表现，eval 模式有几个重要的参数。

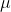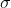• track_running_stats默认为True，train 模式下统计running_mean和running_var，eval 模式下用统计数据作为  和  。设置为False时，eval模式直接计算输入的均值和方差。
• running_mean、running_var：train 模式下的统计量。

也就是说，BN.training 并不是决定 BN 行为的唯一参数。满足BN.training or not BN.track_running_stats就会直接计算输入数据的均值方差，否则用统计量代替。

# 切换到eval模式
bn_layer.train(mode=False)
inference_inputs = create_inputs()
# 输出前后的 running_mean 和 running_var，验证eval模式下不再更新统计量
print(f'bn_layer running_mean is {bn_layer.running_mean}')
print(f'bn_layer running_var is {bn_layer.running_var}')
bn_outputs = bn_layer(inference_inputs)
print(f'Now bn_layer running_mean is {bn_layer.running_mean}')
print(f'Now bn_layer running_var is {bn_layer.running_var}')
# 用之前统计的running_mean和running_var替代输入的running_mean和running_var
_, _, dummy_outputs = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps,
    running_mean, running_var)
assert torch.allclose(dummy_outputs, bn_outputs)

# 关闭track_running_stats后，即使在eval模式下，也会去计算输入的mean和var
bn_layer.track_running_stats = False
bn_outputs_notrack = bn_layer(inference_inputs)
_, _, dummy_outputs_notrack = dummy_bn_forward(
    inference_inputs, bn_layer.weight,
    bn_layer.bias, bn_layer.eps)

assert torch.allclose(dummy_outputs_notrack, bn_outputs_notrack)
assert not torch.allclose(bn_outputs, bn_outputs_notrack)

输出结果如下：

bn_layer running_mean is tensor([-0.0143,  0.0089, -0.0062])
bn_layer running_var is tensor([0.9611, 1.0380, 1.0181])
Now bn_layer running_mean is tensor([-0.0143,  0.0089, -0.0062])
Now bn_layer running_var is tensor([0.9611, 1.0380, 1.0181])

2.2 BatchNormNd 类

包括BatchNorm1d，BatchNorm2d，BatchNorm3d。区别只是检查了输入的合法性，这里简单贴一下BatchNorm2d的实现：

class BatchNorm2d(_BatchNorm):
    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError('expected 4D input (got {}D input)'
                             .format(input.dim()))

BatchNorm1d接受 2D 或 3D 的输入，BatchNorm2d接受 4D 的输入，BatchNorm3d接受 5D 的输入。

3. SyncBatchNorm 的 PyTorch 实现

BN 的性能和 batch size 有很大的关系。batch size 越大，BN 的统计量也会越准。然而像检测这样的任务，占用显存较高，一张显卡往往只能拿较少的图片（比如 2 张）来训练，这就导致 BN 的表现变差。一个解决方式是 SyncBN：所有卡共享同一个 BN，得到全局的统计量。

PyTorch 的 SyncBN 分别在 torch/nn/modules/batchnorm.py 和 torch/nn/modules/_functions.py 做了实现。前者主要负责检查输入合法性，以及根据momentum等设置进行传参，调用后者。后者负责计算单卡统计量以及进程间通信。

class SyncBatchNorm(_BatchNorm):
    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True, process_group=None):
        super(SyncBatchNorm, self).__init__(num_features, eps, momentum, affine, track_running_stats)
        self.process_group = process_group
        # gpu_size is set through DistributedDataParallel initialization. This is to ensure that SyncBatchNorm is used
        # under supported condition (single GPU per process)
        self.ddp_gpu_size = None

    def _check_input_dim(self, input):
        if input.dim() < 2:
            raise ValueError('expected at least 2D input (got {}D input)'
                             .format(input.dim()))

    def _specify_ddp_gpu_num(self, gpu_size):
        if gpu_size > 1:
            raise ValueError('SyncBatchNorm is only supported for DDP with single GPU per process')
        self.ddp_gpu_size = gpu_size

    def forward(self, input):
        if not input.is_cuda:
            raise ValueError('SyncBatchNorm expected input tensor to be on GPU')

        self._check_input_dim(input)

        # exponential_average_factor is set to self.momentum
        # (when it is available) only so that it gets updated
        # in ONNX graph when this node is exported to ONNX.
        # 接下来这部分与普通BN差别不大
        if self.momentum is None:
            exponential_average_factor = 0.0
        else:
            exponential_average_factor = self.momentum

        if self.training and self.track_running_stats:
            self.num_batches_tracked = self.num_batches_tracked + 1
            if self.momentum is None:  # use cumulative moving average
                exponential_average_factor = 1.0 / self.num_batches_tracked.item()
            else:  # use exponential moving average
                exponential_average_factor = self.momentum

        # 如果在train模式下，或者关闭track_running_stats，就需要同步全局的均值和方差
        need_sync = self.training or not self.track_running_stats
        if need_sync:
            process_group = torch.distributed.group.WORLD
            if self.process_group:
                process_group = self.process_group
            world_size = torch.distributed.get_world_size(process_group)
            need_sync = world_size > 1

        # 如果不需要同步，SyncBN的行为就与普通BN一致
        if not need_sync:
            return F.batch_norm(
                input, self.running_mean, self.running_var, self.weight, self.bias,
                self.training or not self.track_running_stats,
                exponential_average_factor, self.eps)
        else:
            if not self.ddp_gpu_size:
                raise AttributeError('SyncBatchNorm is only supported within torch.nn.parallel.DistributedDataParallel')

            return sync_batch_norm.apply(
                input, self.weight, self.bias, self.running_mean, self.running_var,
                self.eps, exponential_average_factor, process_group, world_size)

    # 把普通BN转为SyncBN, 主要做一些参数拷贝
    @classmethod
    def convert_sync_batchnorm(cls, module, process_group=None):
        module_output = module
        if isinstance(module, torch.nn.modules.batchnorm._BatchNorm):
            module_output = torch.nn.SyncBatchNorm(module.num_features,
                                                   module.eps, module.momentum,
                                                   module.affine,
                                                   module.track_running_stats,
                                                   process_group)
            if module.affine:
                with torch.no_grad():
                    module_output.weight.copy_(module.weight)
                    module_output.bias.copy_(module.bias)
                # keep requires_grad unchanged
                module_output.weight.requires_grad = module.weight.requires_grad
                module_output.bias.requires_grad = module.bias.requires_grad
            module_output.running_mean = module.running_mean
            module_output.running_var = module.running_var
            module_output.num_batches_tracked = module.num_batches_tracked
        for name, child in module.named_children():
            module_output.add_module(name, cls.convert_sync_batchnorm(child, process_group))
        del module
        return module_output

3.1 forward

复习一下方差的计算方式： 

单卡上的 BN 会计算该卡对应输入的均值、方差，然后做 Normalize；SyncBN 则需要得到全局的统计量，也就是“所有卡上的输入”对应的均值、方差。一个简单的想法是分两个步骤：

1. 每张卡单独计算其均值，然后做一次同步，得到全局均值
2. 用全局均值去算每张卡对应的方差，然后做一次同步，得到全局方差

但两次同步会消耗更多时间，事实上一次同步就可以实现  和  的计算：

只需要在同步时算好  和  即可。这里用一张图来描述这一过程。

实现时，batchnorm.SyncBatchNorm 根据自身的超参设置、train/eval 等设置参数，并调用_functions.SyncBatchNorm，接口是def forward(self, input, weight, bias, running_mean, running_var, eps, momentum, process_group, world_size): 首先算一下单卡上的均值和方差：

# 这里直接算invstd，也就是 1/(sqrt(var+eps))
mean, invstd = torch.batch_norm_stats(input, eps)

然后同步各卡的数据，得到mean_all和invstd_all，再算出全局的统计量，更新running_mean，running_var:

# 计算全局的mean和invstd
mean, invstd = torch.batch_norm_gather_stats_with_counts(
    input,
    mean_all,
    invstd_all,
    running_mean,
    running_var,
    momentum,
    eps,
    count_all.view(-1).long().tolist()
)

3.2 backward

由于不同的进程共享同一组 BN 参数，因此在 backward 到 BN 前、后都需要做进程的通信，在_functions.SyncBatchNorm中实现：

# calculate local stats as well as grad_weight / grad_bias
sum_dy, sum_dy_xmu, grad_weight, grad_bias = torch.batch_norm_backward_reduce(
    grad_output,
    saved_input,
    mean,
    invstd,
    weight,
    self.needs_input_grad[0],
    self.needs_input_grad[1],
    self.needs_input_grad[2]
)

算出 weight、bias 的梯度以及  ，  用于计算  的梯度：

# all_reduce 计算梯度之和
sum_dy_all_reduce = torch.distributed.all_reduce(
    sum_dy, torch.distributed.ReduceOp.SUM, process_group, async_op=True)
sum_dy_xmu_all_reduce = torch.distributed.all_reduce(
    sum_dy_xmu, torch.distributed.ReduceOp.SUM, process_group, async_op=True)
# ...
# 根据总的size，对梯度做平均
divisor = count_tensor.sum()
mean_dy = sum_dy / divisor
mean_dy_xmu = sum_dy_xmu / divisor
# backward pass for gradient calculation
grad_input = torch.batch_norm_backward_elemt(
    grad_output,
    saved_input,
    mean,
    invstd,
    weight,
    mean_dy,
    mean_dy_xmu
)