Pytorch神经网络拟合抛物线(二次曲线)
本文是利用pytorch中神经网络来对一条抛物线进行拟合,这种拟合相对简单,在很多教材中往往都是用numpy或者自定义的方式求出w和b值来拟合。
class MyCNN(torch.nn.Module):
def __init__(self, in_cheng, hid_cheng, out_cheng):
super().__init__()
self.incheng = torch.nn.Sequential(
torch.nn.Linear(in_cheng, hid_cheng),
torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, hid_cheng),
torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, hid_cheng),
torch.nn.ReLU(),
# torch.nn.Linear(hid_cheng, hid_cheng),
# torch.nn.ReLU(),
# torch.nn.Linear(hid_cheng, hid_cheng),
# torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, out_cheng),
torch.nn.ReLU()
)
def forward(self, x):
x = self.incheng(x)
x.view(-1, n)
return x
上图中用了比较模块化的写法,用到了torch.nn.Sequential(),在每个神经元(torch.nn.Linear)后都跟了ReLU激活函数,输入层数是1层,中间的隐藏层(hid_cheng)是1000,具体隐藏层数是多少可以自己去实验,如果是1的话,效果很差,这个数字大一点会比较好,但是又不能过大,会导致运算时间过长以及其他问题。一般抛物线x(横坐标)是一个一维的Tensor(不好理解,可以认为是c++中的一个一维数组),因此输入层(in_cheng)往往都是1,不是1的话会导致2个矩阵无法相乘问题(就是矩阵论中的第一个矩阵列要和第二个矩阵行要相同才能做乘法)。输出层(out_cheng)一般也是1,是1的话最后可以有一个一维的Tensor(不好理解,可以认为是c++中的一个一维数组),得到的曲线也是一条曲线,吐过输出层为9,那么就会得到二维的Tensor(不妨认为是一个9*那个一维的Tensor)。
输入的x,y如下:
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1).to(device)
y = 6 * x.pow(value_pow) + 1 + 0.2 * torch.rand(x.size()).to(device)
函数是y=6x^2+1,这个比较简单,就是在[-1,1]中得到100个x。
调用GPU:
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
my_net.to(device)
设置损失和优化:
my_optim = torch.optim.SGD(my_net.parameters(), lr=0.001)
my_loss = torch.nn.MSELoss()
训练:
for my_step in range(max_for + 1):
my_y = my_net(x)
my_optim.zero_grad()
loss = my_loss(my_y, y)
loss.backward()
my_optim.step()
if (my_step % 100 == 0):
print(loss)
训练中,记得写法,首先每次进行梯度运算时先清零(不能接着上次的算),损失值loss(你也可以用别的名字,但是一般用这个的更多),后面的函数中,第一个值是预测的,第二个值是真实值loss = my_loss(my_y, y),然后是反向传播(就是迭代求梯度),下一个设置是更新参数空间(具体怎么回事,可以自己搜索一下),if那里的无所谓,只是用来显示loss值是多少。
函数图像:
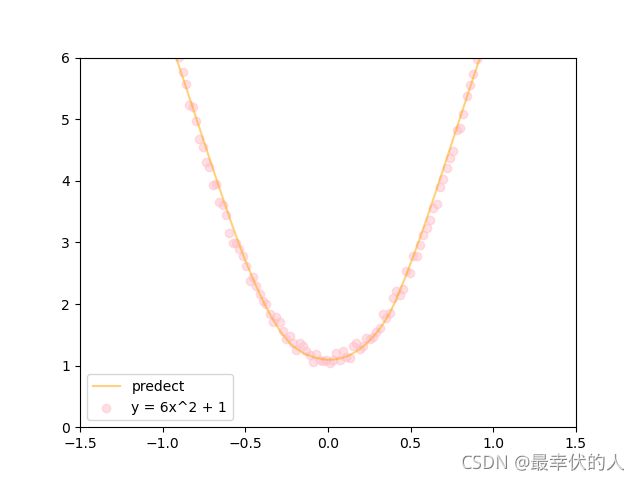
如果函数的输出层为10,结果图:
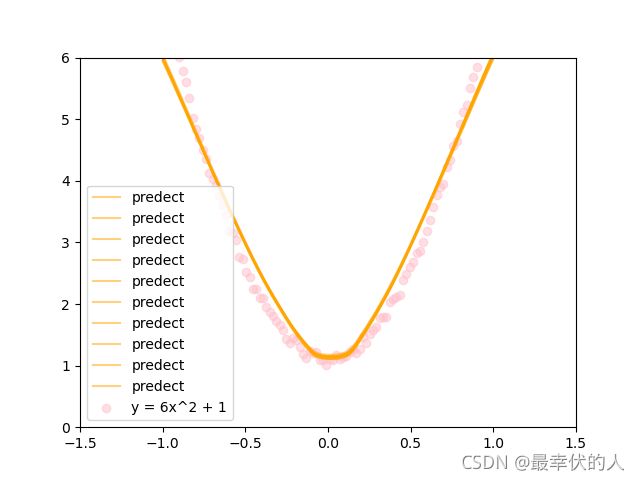
总之,各种参数都可以自己去试一试,会有很大的收获。
完整代码:
import torch
from matplotlib import pyplot as plt
n = 100
max_for = 1000
value_pow = 2
torch.manual_seed(n)
dtype = torch.float
class MyCNN(torch.nn.Module):
def __init__(self, in_cheng, hid_cheng, out_cheng):
super().__init__()
self.incheng = torch.nn.Sequential(
torch.nn.Linear(in_cheng, hid_cheng),
torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, hid_cheng),
torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, hid_cheng),
torch.nn.ReLU(),
# torch.nn.Linear(hid_cheng, hid_cheng),
# torch.nn.ReLU(),
# torch.nn.Linear(hid_cheng, hid_cheng),
# torch.nn.ReLU(),
torch.nn.Linear(hid_cheng, out_cheng),
torch.nn.ReLU()
)
def forward(self, x):
x = self.incheng(x)
x.view(-1, n)
return x
my_net = MyCNN(1, 1000, 1)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
my_net.to(device)
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1).to(device)
y = 6 * x.pow(value_pow) + 1 + 0.2 * torch.rand(x.size()).to(device)
my_optim = torch.optim.SGD(my_net.parameters(), lr=0.001)
my_loss = torch.nn.MSELoss()
for my_step in range(max_for + 1):
my_y = my_net(x)
my_optim.zero_grad()
loss = my_loss(my_y, y)
loss.backward()
my_optim.step()
if (my_step % 100 == 0):
print(loss)
# 可视化结果来了
plt.plot(x.cpu().numpy(), my_y.detach().cpu().numpy(), color='orange', alpha=0.5, label='predect')
plt.scatter(x.cpu().numpy(), y.cpu().numpy(), color='pink', alpha=0.5, marker='o', label='y = 6x^2 + 1') # 真实数据
plt.xlim(-1.5, 1.5)
plt.ylim(0, 6)
plt.legend()
plt.show()
print("y: ")
print(my_y.detach())
如果有哪块写的不对,欢迎指正。