（机器学习）绘制PR曲线

机器学习：绘制PR曲线与ROC曲线

1、PR曲线与ROC曲线的定义

在了解两条曲线之前，先来看下如下的混淆矩阵

	预测结果	+1	-1
真实结果
+1		TP(真正例)	FN(伪反例)
-1		FP(伪正例)	TN(真反例)

在一个二分类问题中

把正例正确判定为正例，表示为TP（true positive）

把正例错误判定为负例，表示为FN（false negative）

把负例正确判定为负例，表示为TN（true negative）

把负例错误判定为正例，表示为FP（false positive）

通过混淆矩阵可以计算出精确率precision 召回率recall ：
$$Precision=TP/(TP+FP)$$

$$Recall=TP/(TP+FN)$$

$$TPR=TP/(TP+FN)$$

$$FPR=FP/(FP+TN)$$

Precision的具体含义其实就是预测为正例的样本中预测正例中所占的比例。

Recall的具体含义就是预测正确的正例的样本在所有真正正例样本中的比例。

TPR的具体含义就是预测正确的正例样本在所有真正正例样本中的比例，跟Recall一样。

TFR的具体含义就是预测正确的反例样本在所有真正反例样本中的比例。

PR曲线

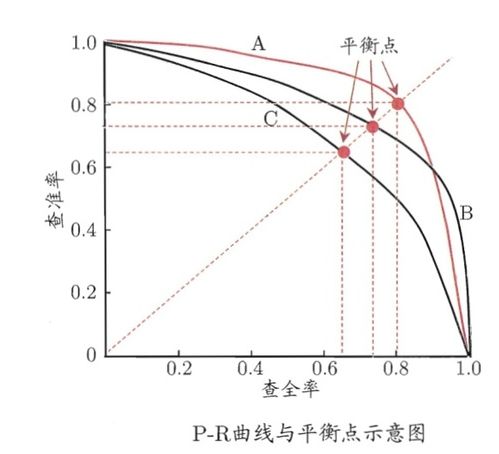
P-R曲线就是Precision与Recall以这两个度量标准分别为纵轴跟横轴绘制的一条曲线，表示在所取的阈值不一样时，对应的precision值与recall值，然后构成一条曲线，要构造一个precision大或者recall大的分类器较为容易，但是比较难保证两者同时成立。

上图所示三条PR曲线中，当Precision=Recall时，取得平衡点（BEP），平衡点越外侧时，此PR曲线对应的学习器效果更好，拥有相对更大的Precision与Recall，所以PR曲线更接近于外侧（或者将另一曲线围住）的学习器效果也是更好的，用上面的图来说，就是曲线C的效果最差，B较好，A是最佳的，A曲线与B曲线有交叉，则可计算重叠面积来比较，明显A的效果比B好。

ROC曲线

ROC代表接收者操作特征（receiver operating characterrestic）

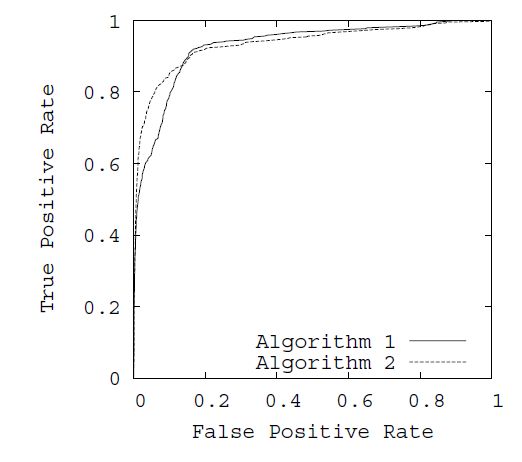
ROC曲线绘图过程与PR曲线类似，就是横轴，纵轴的度量发生变化，横轴是FPR，纵轴是TPR

对于ROC曲线的比较标准，常用AUC(Area Unser the Curve)来评价，即曲线下的面积，这个指标给出的是分类器的平均性能值，并不能代替对整条曲线的观察，一个完美的分类器AUC为1.0而随机猜测的AUC为0.5。

PR曲线与ROC曲线的绘制

使用sklearn里的sklearn.metrics.precision_recall_curve（）与sklearn.metrics.roc_curve来绘制PR曲线，参考博客_precision_recall_curve

其中y_true是样本的标签，y_score是样本的置信度

样本设置如下

y_true = [0, 0, 1, 1, 0, 1]
y_score = [0.1, 0.4, 0.35, 0.8, 0.6 ,0.55]

from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt


y_true = [0, 0, 1, 1, 0, 1]
y_score = [0.1, 0.4, 0.35, 0.8, 0.6 ,0.55]
 
 
precision, recall, thresholds = precision_recall_curve(y_true, y_score)
#print(precision)
#print(recall)
#print(thresholds)

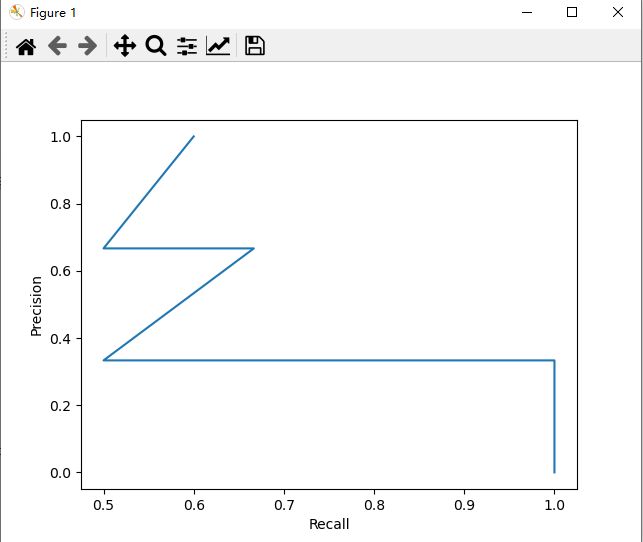
plt.plot(precision, recall)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()


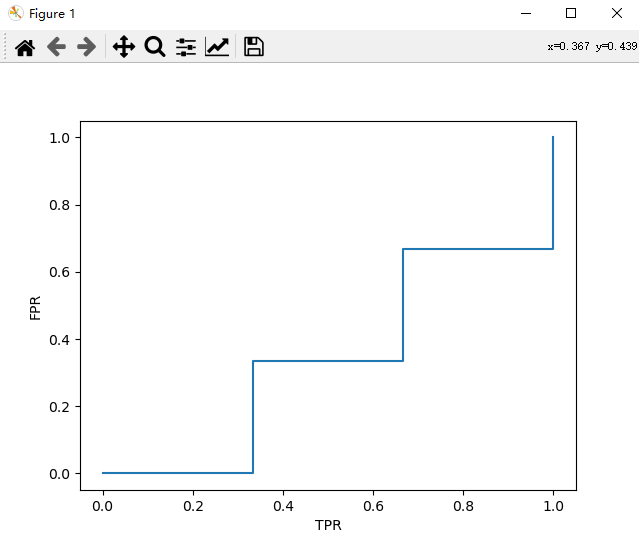
fpr, tpr, thresholds = roc_curve(y_true, y_score, pos_label=1)
plt.plot(tpr, fpr)
plt.xlabel('TPR')
plt.ylabel('FPR')
plt.show()