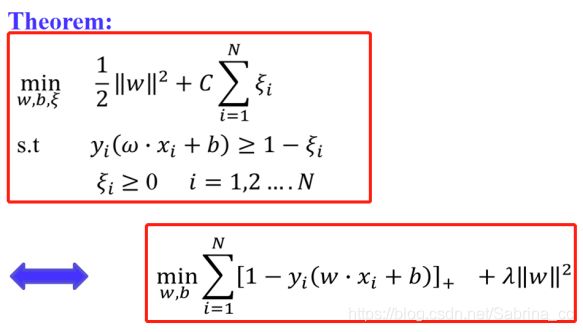机器学习-支持向量机 -- 软间隔SVM和非线性SVM

上篇文章讲了硬间隔SVM，利用间隔最大化求最优超平面和决策函数

-Q:现实中, 很难找到一个超平面使得训练样本在特征空间中线性可分; 同时一个线性可分的结果也很难断定是否是有过拟合造成的.

-A:引入”软间隔”的概念, 允许支持向量机在一些样本上不满足约束.

---

一、软间隔SVM

1. 松弛变量

2. 软间隔SVM模型

3. 使用对偶求解

4. 软间隔SVM算法

5. 软间隔支持向量

6. 合页损失函数

二、非线性SVM（Nonlinear SVM and kernels）

1. 解决思路：

2. 核函数

3. 非线性支持向量机算法

4. 非线性SVM例题

5. 核函数的选择

---

一、软间隔SVM

 支持向量机的一般思想是:使超平面与每个类的最近实例之间的距离最大。

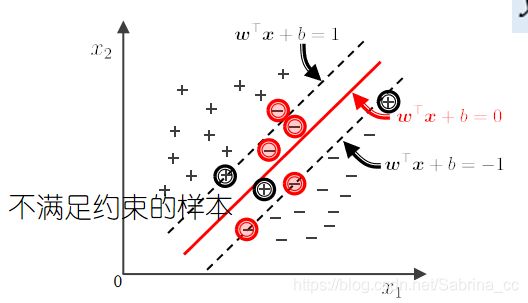
 在大多数情况下，训练集是不可分离的，不等式约束是不满足的。一般来说，训练集中存在一些异常值。这些数据点叫做奇异点。

   对于很难找到找平面合理分开数据集的情况, 如果数据不是线性可分的（含有噪声点）怎么办?因此引入了软间隔SVM，对这些样本引入松弛变量，对这些数据点进行变化，从而使他们可分。

1. 松弛变量

训练集T（线性不可分数据集）

支持向量机可以忽略异常值，找到具有最大边界的超平面。因此，SVM对异常值具有较强的鲁棒性。

C：叫做惩罚参数，用来平稳正则项和误差项，若C小，则对误分类的惩罚小。

两层含义：让间隔尽量大，让误差尽量小

从而建立原始软间隔SVM的模型：

2. 软间隔SVM模型

是线性不可分的SVM

假设他的解最优超平面为 w* x + b* = 0

这个模型包含上篇文章的模型，使用更广泛

这实质也是一个凸二次规划问题（求解可以使用对偶问题）

那么如何求解该问题？

3. 使用对偶求解

使用拉格朗日函数，对于每个约束条件引入一个松弛变量（分别是a和u）

注意：变量的系数为负（对应约束条件的g(x)<0是正号）

使用对偶问题求解的思路：求拉格朗日函数--求导

其中使用拉式理论可以计算出w* 和b*

(由于两项乘机为0，一项 不为零，另一项一定为0 化简假设的情况)

从而解出 w* 和b*

(此处b*可能取值不唯一，选一个即可)

从而进一步解出最优超平面和决策函数

4. 软间隔SVM算法

输入：训练集T

输出：分离超平面 决策函数

求解思路：

5. 软间隔支持向量

有4中情况：在边缘带上；在间隔超平面内；在超平面上；是误分类点

对于不是支持向量，对该模型没有什么影响；对于支持向量，对超平面的确定影响很大

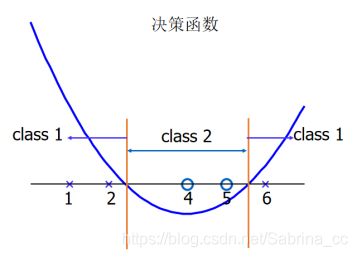
6. 合页损失函数

在机器学习中，合页函数训练分类器的一个损失函数，用来最大化间隔距离，常用于SVM中

被正确分类的，且函数间隔大于1，则loss为0，否则loss之和就是误差

上述式子和软间隔SVM是等价的，如何证明？

因此两者是等价的：

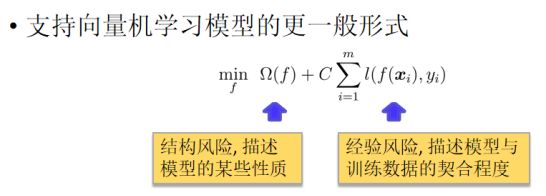
软间隔SVM模型和机器学习的一般模型是等价的。

多种损失函数的比较

总结：

对于线性可分问题：建立超平面--求w,b--建立优化模型--硬间隔--凸二次规划--对偶问题--支持向量

对于线性不可分问题：增加松弛变量--建立优化模型--软间隔--凸二次规划--对偶问题--支持向量

那么对于非线性问题怎末办？（核技巧）

二、非线性SVM（Nonlinear SVM and kernels）

（似乎可以用一个弧形划分）

1. 解决思路：

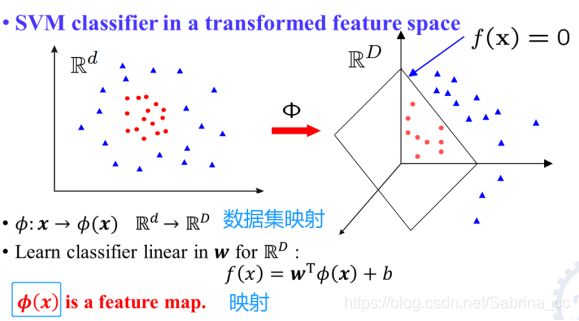
转换（1）坐标变换；（2）投影（变换到另一个空间，在高维空间找超平面）

但是，会不会增加了复杂性？并没有，因为可以使用核函数

因此映射之后，分类器和优化问题就变成了：

2. 核函数

引入核函数替换内积，从而得到：

特殊的核函数

其中，线性核函数说明：软间隔SVM是非线性SVM的特例

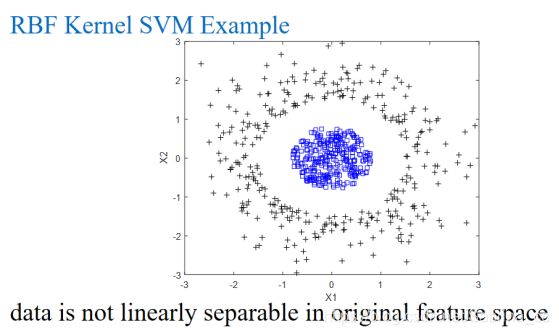
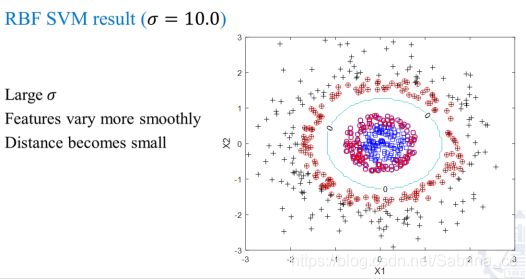
高斯核函数应用最多，镜像机函数分类器（RBF SVM）图示：

3. 非线性支持向量机算法

输入：训练集T

输出：决策函数

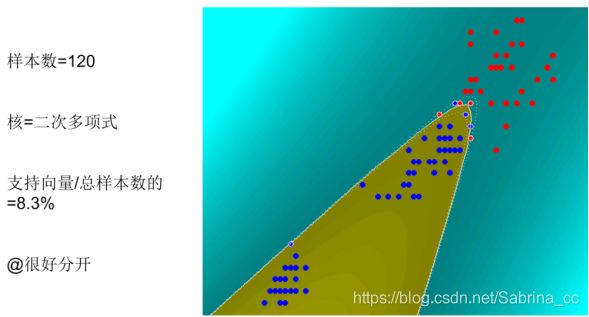
解决思路：选择核函数K和C---构造二次规划问题---得到a*----特殊的aj* ,取0< aj

总结：软间隔SVM是K为线性时的特例；硬间隔SVM是软间隔SVM的特例

4. 非线性SVM例题

   

5. 核函数的选择

核的选择对结果有很大的影响。但是核的选择却没有统一的方法，大多要靠经验

总结：

硬间隔SVM（最大化硬间隔 线性分类器）

软间隔SVM（最大化软间隔 线性分类器）

非线性SVM（核技巧 最大化软间隔 非线性分类器）

 

下一篇继续讲解SVM模型的使用，多分类情况，决策树