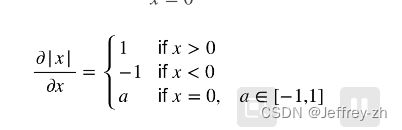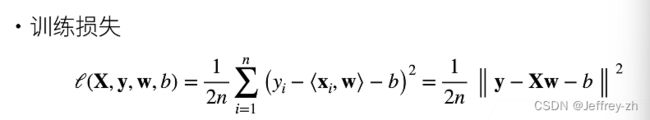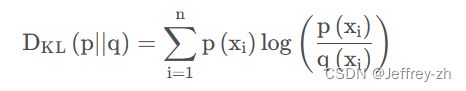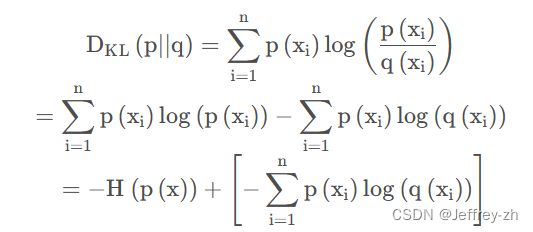机器学习笔记（李沐6-11）
六.矩阵计算
1.亚导数：将导数扩展到不可微的函数
举个例子, 假设是y=|x|,在 x = 0 x=0 x=0时的导数不存在, 但是我们可以假设其存在, 令其在1和-1之间
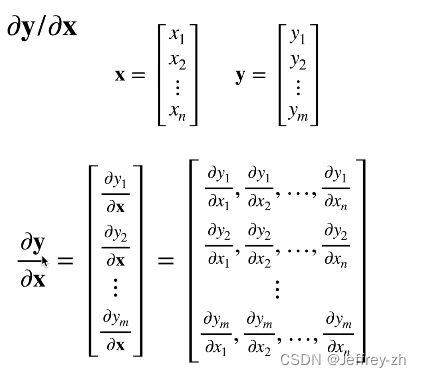
2.将导数拓展到向量
3.向量与向量求导会得到矩阵
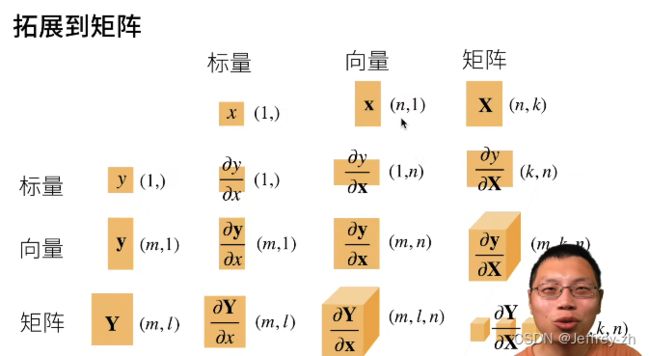
4.拓展到矩阵
七．自动求导
1.求导类型：一个函数在指定值上求导，分符号求导，数值求导
2.计算图：将代码分解成操作子，计算表示为无环图
3.自动求导步骤：正向积累，反向传递
（1）计算复杂度：正向积累复杂度O（n），反向累计内存复杂度O（1），正向内存复杂度O（n）
（2）代码实现PyTorch提供了autograd包来自动根据输入和前向传播构建计算图，其中，backward函数可以很轻松的计算出梯度。如果想使用autograd包让它们参与梯度计算，则需要在创建它们的时候，将.requires_grad属性指定为true。
注：在pytorch中，只有浮点类型的数才有梯度，因此在定义张量时一定要将类型指定为float型。
八.线性回归+基础优化算法
1.线性模型可以看成是单层神经网络，线性回归有显示解，但机器学习很少设计有显示解的计算
2.优化方法：
*梯度下降：
挑选初始值w0，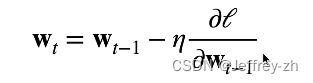
不断更新Wt找到一个最优解。
为学习率，步长的超参数；不能太小，步长有限太慢，不能太大，可能一直震荡不能下降。
九.Softmax回归 + 损失函数 +图片分类数据集
1.回归估计连续值，分类预测离散类别
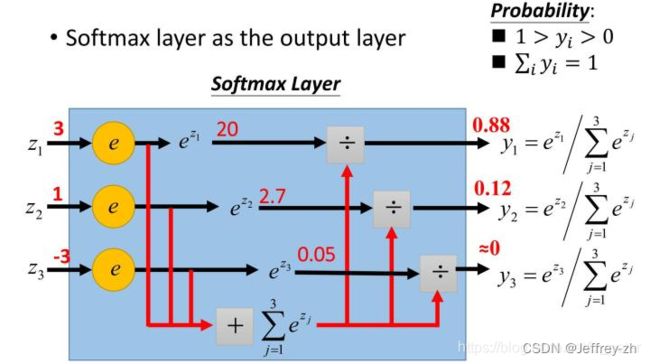
2.Softmax函数
1）将预测结果转化为非负数
我们可以知道指数函数的值域取值范围是零到正无穷。softmax第一步就是将模型的预测结果转化到指数函数上，这样保证了概率的非负性。
2）各种预测结果概率之和等于1
为了确保各个预测结果的概率之和等于1。我们只需要将转换后的结果进行归一化处理。方法就是将转化后的结果除以所有转化后结果之和，可以理解为转化后结果占总数的百分比。这样就得到近似的概率。
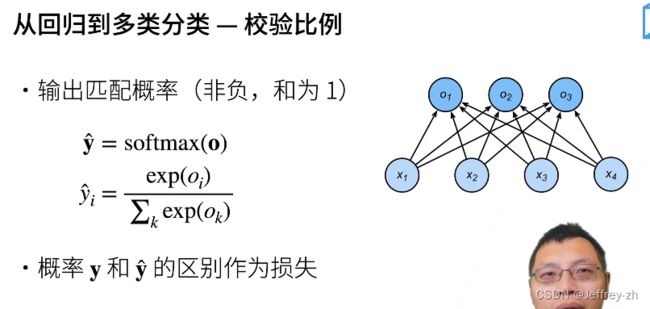
3.校验比例
比较真实y的概率和预测的y的概率，两者作差作为损失。
4.交叉熵：
在线性回归问题中，常常使用MSE(Mean Squared Error)作为loss函数，而在分类问题中常常使用交叉熵作为loss函数。
（1）信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。设某一事件发生的概率为P(x)，其信息量表示为：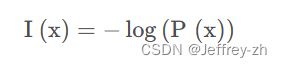
（2）信息熵
信息熵也被称为熵，用来表示所有信息量的期望。期望是试验中每次可能结果的概率乘以其结果的总和。
（3）相对熵（KL散度）
如果对于同一个随机变量 X有两个单独的概率分布P(x)和 Q ( x )则我们可以使用KL散度来衡量这两个概率分布之间的差异。
在机器学习中，常常使用 P ( x )来表示样本的真实分布， Q ( x )来表示模型所预测的分布。KL散度越小，表示P(x)与Q(x)的分布更加接近，可以通过反复训练Q(x)的分布逼近 P ( x )。
（4）交叉熵：首先将KL散度公式拆开：前者 H ( p ( x ) )表示信息熵，后者即为交叉熵，KL散度 = 交叉熵 - 信息熵
5.Softmax注意事项
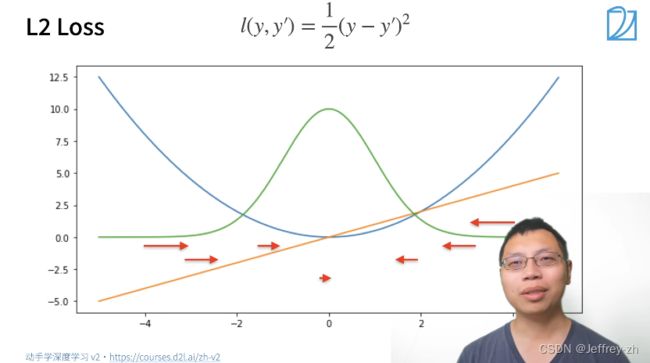
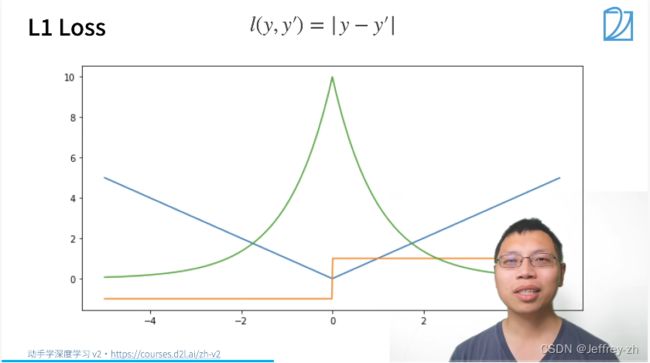
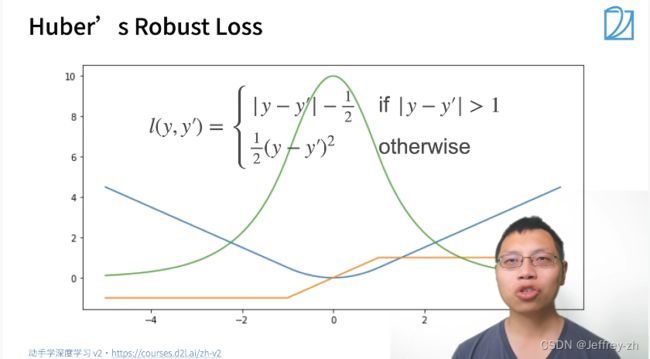
5.常用损失函数：
十．多层感知机（MLP）
1.感知机是二分类问题，softmax回归输出概率。
2.感知机限制：
感知机不能拟合XOR函数，它只能产生线性分割面
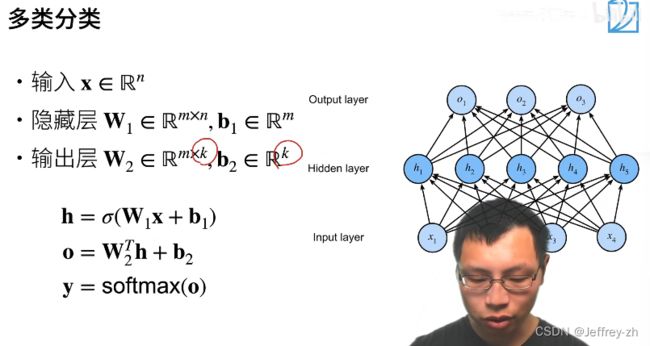
3.多层感知机：
4.激活函数必须要非线性的原因：
线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐 藏 层 的 神 经 网 络”。这 里 我 们 考 虑 把 线 性 函 数 h(x) = cx 作 为 激 活函 数,把 y(x) = h(h(h(x))) 的 运 算 对 应 3 层 神 经 网 络 A 。这 个 运 算 会 进 行y(x) = c × c × c × x 的乘法运算,但是同样的处理可以由 y(x) = ax (注意,a =c^3)这一次乘法运算(即没有隐藏层的神经网络)来表示。如本例所示,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
激活函数主要用来避免层数的塌陷，输出不需要激活函数
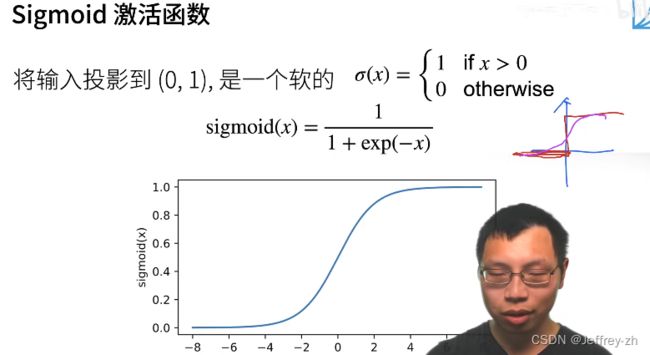
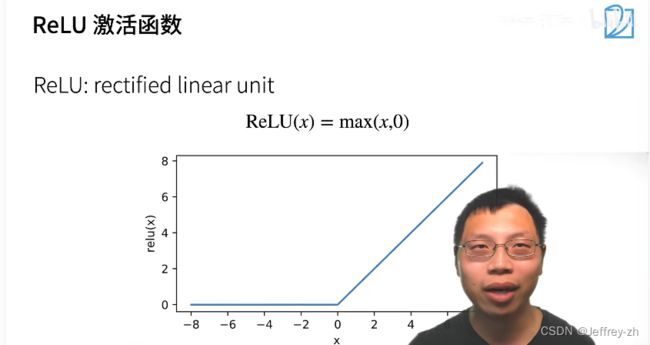
5.常见激活函数：
*ReLU优势：不用计算自然指数，简单，成本少
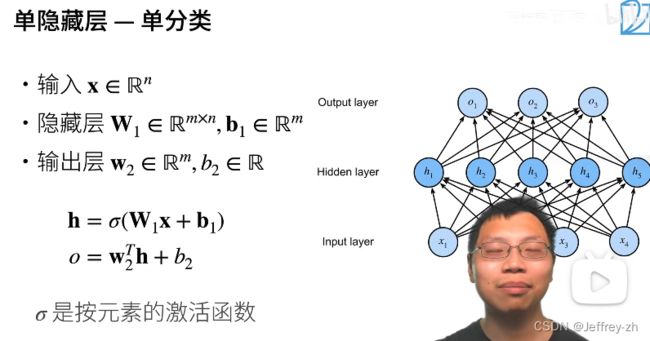
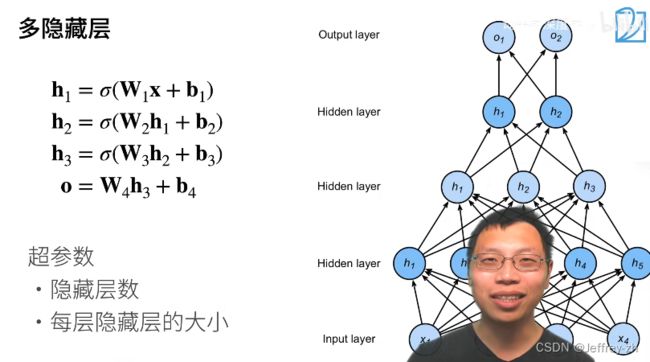
6.单隐藏层和多隐藏层示例：
7.为什么要用隐藏层？线性模型可能会出错
例如，我们想要根据体温预测死亡率。 对于体温高于37摄氏度的人来说，温度越高风险越大。 然而，对于体温低于37摄氏度的人来说，温度越高风险就越低。 在这种情况下，我们也可以通过一些巧妙的预处理来解决问题。 例如，我们可以使用与37摄氏度的距离作为特征。
我们的数据可能会有一种表示，这种表示会考虑到我们在特征之间的相关交互作用。 在此表示的基础上建立一个线性模型可能会是合适的， 但我们不知道如何手动计算这么一种表示。 对于深度神经网络，我们使用观测数据来联合学习隐藏层表示和应用于该表示的线性预测器。
十一.模型选择+过拟合和欠拟合
1.训练误差：模型在训练数据上的误差
泛化误差：模型在新数据上的误差
2.数据集
（1）验证数据集：用来评估模型好坏
有时一半用来训练；一半用来验证（未参与训练）
不同神经网络在训练集上训练结束后,通过验证集来比较判断各个模型的性能.这里的不同模型主要是指对应不同超参数的神经网络,也可以指完全不同结构的神经网络
（2）测试数据集：只用一次的数据集，不能用来调超参数
Eg.未来的考试，出价的房子的实际成交价
最正常的做法:使用训练集来学习，并使用验证集来调整超参数。当在验证集上取得最优的模型时，此时就可以使用此模型的超参数来重新训练（训练集+验证集），并用测试集评估最终的性能。
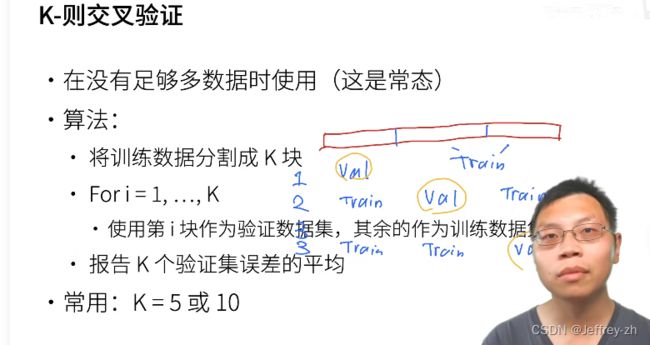
3.K-则交叉验证：在没有足够多数据时使用
