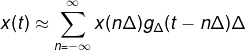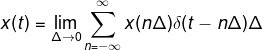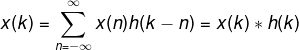OpenCV中的图像金字塔(高斯金字塔、拉普拉斯金字塔)

      最近在看关于数字图像的知识点，目前在图像金字塔部分，实在是懒得用手作笔记了，就以其中比较出名的“高斯金字塔”和“拉普拉斯金字塔”为例，基于OpenCV的源代码作解析存个档；毕竟属于基础部分，以后有需要就当接口调用吧；有写的不对需要改正的地方，还请大家指出，谢谢。

一、金字塔

1.何为图像金字塔？

      图像金字塔是图像中多尺度表达形式的之一，最主要用于图像的分割，是一种以多分辨率来解释图像的有效但概念简单的结构。图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状从低(下)到高(上)排列的，分辨率逐步降低的图像集合。

具体以下示例图和流程图： 

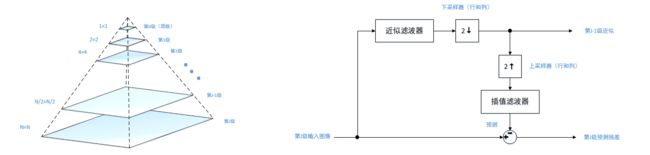图像金字塔分层                                                                                                            模板金字塔流程图

2.何为高斯金字塔？

      高斯金字塔顾名思义，基于模板金字塔的构建的方式引入指定的低通高斯滤波（空间域）并结合下采样的迭代方式进行层次之间的计算；（高斯金字塔底部是第0级）

      而拉普拉斯金字塔恰好与高斯金字塔相反，拉普拉斯金字塔依赖于高斯金字塔构建的图层；当高斯金字塔形成之时，我们需要对高斯金字塔的每一层进行上采样，形成该图层对应的近似预测图像，求去它们之间的差值，得到就是拉普拉斯金字塔该层次的图像；也就是说，高斯金字塔由下至上构建，而拉普拉斯金字塔又上至下构建（高斯金塔要比拉普拉斯金字塔多构建一次，用于顶层差值求取）；得到的拉普拉斯金字塔起到预测残差的作用。

具体以下示例图和流程图：

高斯金字塔                                                                                   高斯金字塔和拉普拉斯金字塔流程图

---

二、金字塔构建流程

1. 高斯金字塔的构建

1. 将原始图像与低通高斯滤波矩阵做卷积处理
2. 利用基数为2的下采样（删除偶数行和偶数列）得到维数减半的上一级图像

---

1.1 低通高斯滤波

      "滤波"一词借用于频率域处理，"滤波"是指接受（通过）或拒绝一定的频率的成分。低频的滤波器成为低通滤波器，其最终的效果是模糊（平滑）一幅图像。

      数值图像处理中，低通高斯滤波可以以不同的形式作用于空间域（线性）和频率域。第一种是属于空间滤波器（也被称为高斯模板、高斯核、高斯掩模、高斯窗口），第二种方法是通过傅里叶变换后进行操作。本文涉及到的是第一种平滑空间滤波器。

      常用的平滑线性空间滤波器有均值滤波以及高斯滤波等。均值滤波使用模板内所有像素的平均值代替模板中心像素灰度值，这种方法易收到噪声的干扰，不能完全消除噪声，只能相对减弱噪声，且存在着不希望有的边缘模糊负面效应；为了减少平滑处理中的模糊效应，得到更加自然的平滑效果，需要适当加大模板中心点的权重；随着距离中心点的距离来增减控制权重占比大小，基于这样的考虑形成的模板即为高斯模板。

       常用的高斯模板核通常是3×3，5×5的奇数矩阵，根据OpenCV提供的代码为例，采用5×5的模板如下（令右侧矩阵为M，左侧为归一化系数）：

 

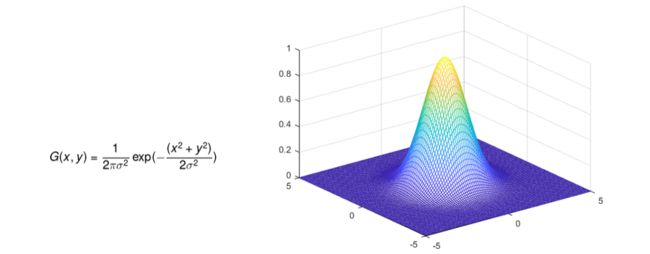
      该高斯模板核矩阵中的参数是通过二维高斯函数，即二维正态分布密度函数求得的，回忆一下（由一维延伸到二维），具体如下。

一维高斯函数，形式如下：

一维高斯函数

二维高斯函数，形式如下：

二维高斯函数（均值u=0）

---

1.2 高斯模板的实现

      高斯模板正是将连续的二维高斯函数的离散化表示，因此任意大小的高斯模板都可以通过建立一个的矩阵M(m×n)，得到其位置的参数可如下确定：

     

      此公式基于Matlab的实现，因此i和j的起始为1非0（数组索引必须为正整数或逻辑值）；基于VS的实现，i和j的起始为0（不要带入-1的参数）；k为每个方向距离该方向中心的距离，即。

获取OpenCV中smooth.dispatch.cpp的getGaussianKernel函数的源码：

Mat getGaussianKernel(int n, double sigma, int ktype)
{
    CV_Assert(n > 0);
    const int SMALL_GAUSSIAN_SIZE = 7;
    static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
    {
        {1.f},                                                                     //1×1
        {0.25f, 0.5f, 0.25f},                                                      //3×3
        {0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},                                  //5×5
        {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}   //7×7
    };

    const float* fixed_kernel = n % 2 == 1 && n <= SMALL_GAUSSIAN_SIZE && sigma <= 0 ?
        small_gaussian_tab[n>>1] : 0;

    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(n, 1, ktype);
    float* cf = kernel.ptr();
    double* cd = kernel.ptr();

    double sigmaX = sigma > 0 ? sigma : ((n-1)*0.5 - 1)*0.3 + 0.8;
    double scale2X = -0.5/(sigmaX*sigmaX);
    double sum = 0;

    int i;
    for( i = 0; i < n; i++ )
    {
        double x = i - (n-1)*0.5;
        double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);
        if( ktype == CV_32F )
        {
            cf[i] = (float)t;
            sum += cf[i];
        }
        else
        {
            cd[i] = t;
            sum += cd[i];
        }
    }

    CV_DbgAssert(fabs(sum) > 0);
    sum = 1./sum;
    for( i = 0; i < n; i++ )                            //归一化
    {
        if( ktype == CV_32F )
            cf[i] = (float)(cf[i]*sum);
        else
            cd[i] *= sum;
    }

    return kernel;
}

代码实现矩阵：

#include
#include

using namespace cv;
using namespace std;

int main()
{
	Mat g, g1, g2;
	g= getGaussianKernel(5, 0, CV_32F);    //size,sigma,type
	g1 = g * g.t();                        //g * g的转置得到二维高斯卷积核
	cout << g1 << endl;
	g2 = g * g.t() * 256;                  //归一化右侧整数矩阵
	cout << g2 << endl;
	cin.get();
	return 0;
}

计算出来的高斯模板参数为：

高斯模板矩阵和矩阵M

• 当第二个参数sigma的取值为0时，getGaussianKernel函数中已经指定了1，3，5，7这四个模板的参数，为的是调用常用模板取固定整型参数，去除小数点也方便运算；
• 当第二个参数sigma的取值不为0时，getGaussianKernel函数将按照指定sigma值代入下两行代码运算： 

double x = i - (n-1)*0.5;          //相当于式中 i-k=i-(n-1)/2
double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);  

上两行代码对应了上述二维高斯函数（不带参数-1）的实现，其中滤去了系数，是因为在下面代码作归一化处理时，可以消除该权重，因此可以省去加快计算速度。

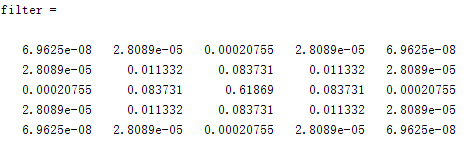
获取Matlab中的fspecial函数：

 filter=fspecial('gaussian',5,0.5);    //mood,size,sigma

取sigma=0.5

---

*关于标准差(sigma)的取值和归一化处理做个两个注释：

1. 标准差(sigma)

      当标准差取不同的值时，二维高斯函数的形状会有很大的变化：如果标准差选择过小，偏离中心的所有像素的权重将会非常小，相当于加权和影响基本不考虑邻域像素的作用，这样滤波操作退化为图像的点运算，无法起到平滑噪声的作用；相反如果标准差选择过大，而邻域相对较小，这样在邻域内高斯模板将会退化为平均模板；因此在实际应用中选择合适的标准差非常重要。

取sigma=0.5                                                                                                                                                 取sigma=5

 2.归一化

       不难看出，在矩阵核的左边存在一个系数，它是归一化的象征;归一化的目的：对灰度级为常数的图像区域，高斯模板的响应和必须为1。若小于1，像素值发生偏移，产生了误差，邻域像素之间的差值将减小；若大于1，存在超过像素上限（255）的可能，形成局部亮度。因此要对初始形成的模板进项归一化处理，且也存在提高整体像素精度的作用。

---

 2.1 图像卷积

      我们依然采用延伸的思维从一维过渡到二维图像卷积，先来看下连续信号的卷积：

 1.连续信号的卷积

      对于任意波形的信号都可以分割成许多相邻的矩阵脉冲，代表了脉冲的宽度，对于时刻的矩形脉冲，其高度即的值为。

用窄脉冲之和近似表示任意信号                                                                                            门函数以及高度（强度）为1的门函数

      无穷多个矩形脉冲的叠加可用来近似原信号，即

      显然，当脉冲宽度越窄，近似程度就越高，就越逼近原信号（类似于高数中的经典积分思想）；当极限的情况下，高度在上升，但面积始终保持为1，因此们函数可表示为由强度形式表达的单位冲激函数,上式变换为

      我们用表示，表示，求和变成连续新变量的卷积积分

• 表明任意波形的信号可以表示为无限多个强度为的单位冲激信号的积分
• 表明任意波形的信号都可以分解为连续的加权（延迟）单位冲激信号之和
• 对于连续信号而言，卷积是一种特殊的积分运算，它的整个过程就是一个函数固定不动，另一个函数先以y轴为对称轴翻转，然后不断执行相乘，积分

 2.离散信号的卷积

       离散时间信号是连续时间信号经过离散化（即取样）的结果，即连续卷积积分离散化为

• 表明任一离散信号均可表示为单位函数的延时加权和的形式

      根据线性时不变系统的零状态响应叠加性和时不变性，则离散系统对零状态响应为,把得到的零状态响应称为卷积和或离散卷积，记为

• 对于上式离散信号求卷积和而言，它的整个过程就是一个一维序列点集合和另一个一维序列点集合反向（翻转）对应乘积的和
• 在此基础之上，拓展到二维（有限范围k内），便有了二维离散卷积，即图像卷积

3.图像卷积

      在执行线性空间滤波时，存在两个近似的概念：一个是"相关"，另一个是"卷积"。

• "相关"是滤波器模板移过图像并计算每个位置乘积之和的处理
• "卷积"是模板先旋转180°，再将滤波器模板移过图像并计算每个位置乘积之和的处理

      "卷积"的基本特性是与单位函数的卷积和仍然是本身，即

      基于以上这一点，我们延伸到二维图像中作卷积(mode:same)，我们令模板与同模板尺寸大小，除中心点像素点为1，其余点为0的矩阵进行"相关"运算，得到的结果是在中心点位产生该模板的一个旋转180°的版本。因此，如果我们预先旋转模板，并执行相同的滑动乘积求和的操作，就能得到希望的结果（中心点为模版矩阵），也契合公式的求取。但如果滤波器模板是对称的，那么作"相关"和"卷积"运算将得到相同的结果，高斯模板正是如此。 

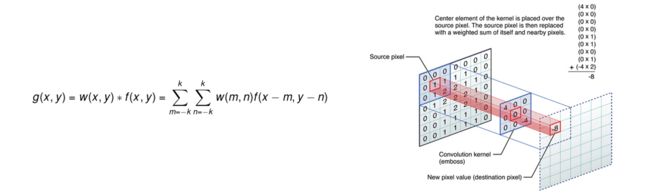图像卷积公式和图像卷积运算（same mode）

      我们也可以从另一个角度举例说明，图像卷积的模板需要先旋转180°；将二维卷积公式展开代入求取特定的值，有

 

原图像坐标和未旋转的3×3的模板坐标

       通过展开式和上图明显能看出要想实现滑动乘积求和，要先将模板w旋转180°即可；对于超出原图像边界的像素值默认赋0。

---

3.1 下采样

       下采样用于减半计算得到的近似及上一层空间维数的图像，下采样操作可视为删除偶数行和偶数列的像素点，赋给新的矩阵序列

       根据OpenCV官方提供的代码，pyrDown()函数专门用于图像的下采样计算（包含了高斯模糊的卷积运算，模板参数大小默认为5×5的）：

pyrDown()函数原型
1.  void cv::pyrDown(InputArray src,                       //待下采样的图像 
2.                   OutputArray dst,                      //输出下采样后的图像
3.                   const Size & dstsize = Size(),        //输出图像尺寸（限制），默认是N/2
4.                   int borderType = BORDER_DEFAULT)      //像素边界外推方式，默认即可

      至此，我们反复的迭代计算（一般金字塔4~5层），便形成了高斯金字塔（具体图片与拉普拉斯金字塔一并给出）。

---

2. 拉普拉斯金字塔的构建

1. 利用基数为2的上采样（在偶数行和偶数列补0）作用在高斯N+1级图像上（尺寸与N级高斯图像一致）
2. 对上采样后图像进行高斯模糊（高斯模板核*4）
3. 将模糊后的图像与原N级高斯图像作差值运算，得到第N级的拉普拉斯图像

---

2.1 上采样

      上采样用于翻倍计算得到的近似同下一层空间维数的图像，下采样操作可视为在偶数行和偶数列的像素值赋0（与下采样形成互补操作），赋给新的矩阵序列

      根据OpenCV官方提供的代码，pyrUp()函数专门用于图像的上采样计算（包含了高斯模糊的卷积运算，5×5的模板参数*4）：

pyrUp()函数原型
1.  void cv::pyrUp(InputArray src,                       //待上采样的图像 
2.                 OutputArray dst,                      //输出上采样后的图像
3.                 const Size & dstsize = Size(),        //输出图像尺寸（限制），默认是N*2
4.                 int borderType = BORDER_DEFAULT)      //像素边界外推方式，默认即可

      至此，我们反复的迭代计算，记得作减法运算，便形成了拉普拉斯金字塔。 

---

*关于模板核*4和模板插值滤波器做个两个注释：       

 1.模板核*4

      对于上采样后需要模糊的高斯模板核*4，很多博主都没详细说明，我的理解是：符合归一化。采用5×5的模板参数落在对应的像素点上，其中存在大量赋值为0的像素点（这些点的权重相当于不作用），无论是对应原矩阵中奇0偶数、偶0奇数、奇数偶0、偶数奇0，非0像素点对应的权重和一定满足，所以将原有归一化系数*4=1/64，满足归一化的作用。

2.模板插值滤波器

      对于内插滤波器，常用的包括最邻近插值法、双线性插值法、双三次插值法，其效果也是呈明显的递增，消除了锯齿特征也保留了图像的细节，毕竟拟合的点数增多了随之而来的是计算时间也增加了；在OpenCV大部分内嵌插值法的函数中和商业用途中多采用双线性插值法，这也是在计算时间和质量之间寻求到的不错的折中选择。

3种插值法示意图

---

      最后，给出高斯金字塔和拉普拉斯金字塔作为完结（附上最经典的Lena图吧，哈哈哈）。

高斯金字塔

拉普拉斯金字塔

---

三、金字塔实现代码

      略(●'◡'●)

---

参考文献：

1.https://www.cnblogs.com/shine-lee/p/9671253.html

2.https://blog.csdn.net/naruhina/article/details/104729037/

3.数字图像处理（冈萨雷斯）

4.数字图像处理和机器视觉（Visual C++与Matlab实现）