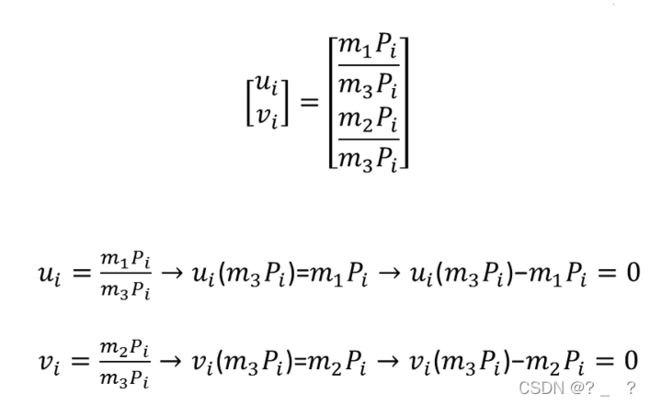笔记:三维重建大作业1-相机标定
(个人理解,若有错误,请不吝指出,谢谢!)
目录
前言:
一、三维空间到照片的映射原理
二、相机标定基于python的opencv
三、参考资料
前言:
摄像机为什么需要标定?
原因有二:
1.现代摄像机都是透镜摄像机,其会产生径向畸变,所以需要算法来矫正
2.制造工艺的误差会导致点对点映射的一些偏差
一、三维空间到照片的映射原理
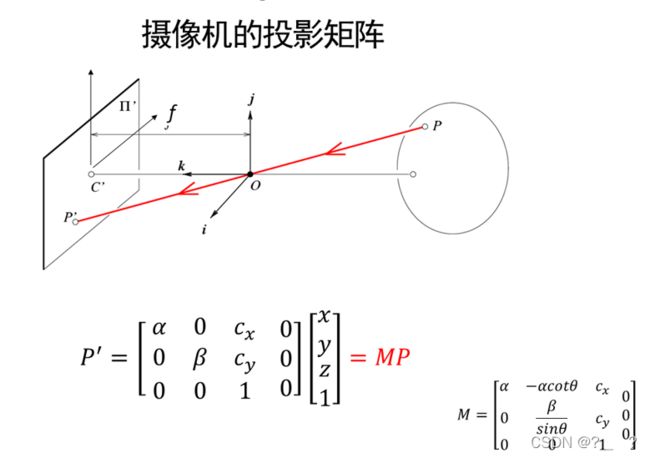
P点为空间坐标,P'为二维图像上的点,我们使得P点为齐次坐标下的点则其坐标为[x,y,z,1],这样就形成了线性关系,P'=MP。M就称为投影矩阵,其中M中的参数皆为摄像机的内部参数值,为常数。
我们上述所用的坐标轴是o-jki,为了统一和方便描述空间点,引入了世界坐标系Ow-JwKwIw,K[I,0]即为上述M矩阵(3*4)为内部参数,此坐标系与原来的坐标系相比,是通过对其平移、旋转得到的,R和T则为旋转和平移向量,为外部参数。
有了变换关系,所以我们就可以求投影矩阵了。首先是相机的内部参数其自由度为5,旋转和平移6个自由度,一共11个未知数那么我们至少需要11个方程,则至少需要11对点。
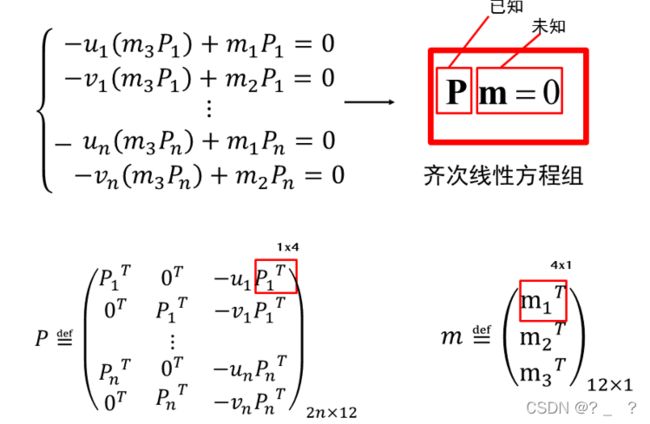
上图,我们列出方程,把M矩阵拆为m1,m2,m3三个向量。
再将方程转化为已知矩阵和未知向量相乘的形式,由于选取的点多于11个,就造成了方程个数大于未知数的问题,会出现奇异值分解,所以会有迭代求解的过程。(具体求解目前还不太懂)
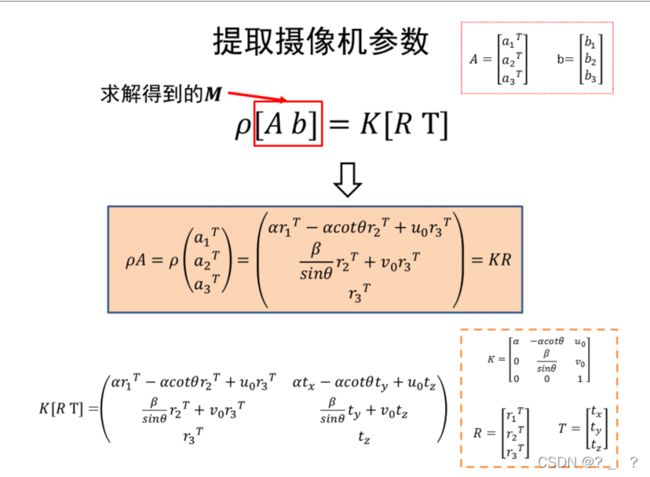
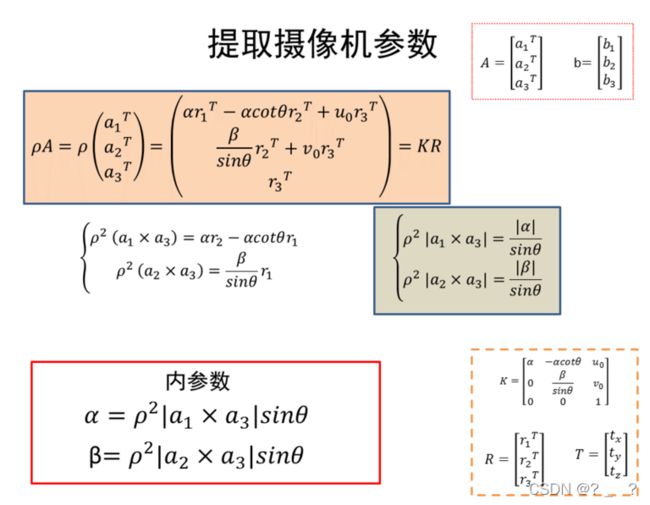
得到了M矩阵,我们现在就可以开始求内部和外部参数了。ρ为一个系数,由于经过M对应关系得到的点不是唯一的,在投影的那条线上均可,为了使其唯一对应则加入系数。
将M矩阵拆成A矩阵和b向量的样式,ρA=KR,通过点乘,叉乘,和取模等一些数学计算则可得到内参数。(俺对这些数学计算也一知半解)
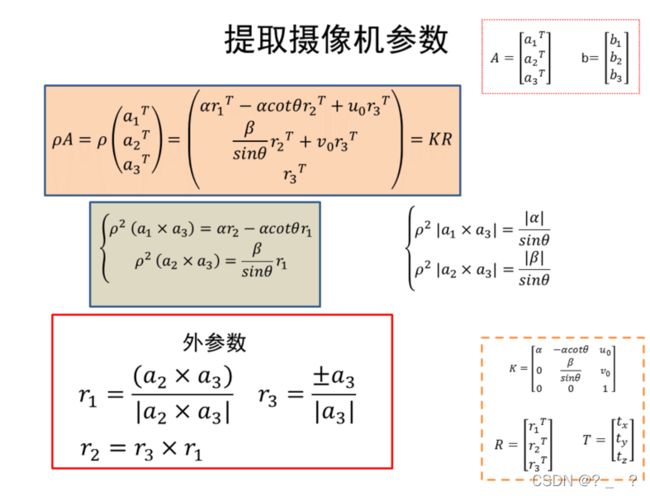
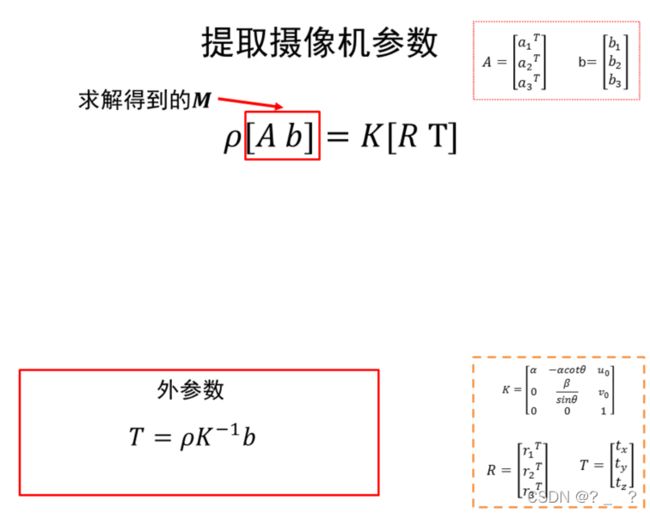
同样的方法,外参数旋转向量与平移向量这些外参数,其公式及其推导如上图所示。
二、相机标定基于python的opencv
本次实验的内容是单平面棋盘格的摄像机标定方法,张正友相机标定法。
本次实验使用的手机型号为:HUAWEI Mate 40E
所用棋盘如下:
拍摄照片:
代码如下:
import cv2
import numpy as np
import glob
# 设置寻找亚像素角点的参数,采用的停止准则是最大循环次数30和最大误差容限0.001
# criteria:迭代停止的模式选择,这是一个含有三个元素的元组型数。格式为(type,max_iter,epsilon)
# 其中,type又有两种选择:
# —–cv2.TERM_CRITERIA_EPS :精确度(误差)满足epsilon停止。
# —- cv2.TERM_CRITERIA_MAX_ITER:迭代次数超过max_iter停止。
# —-cv2.TERM_CRITERIA_EPS+cv2.TERM_CRITERIA_MAX_ITER,两者合体,任意一个满足结束。
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 获取标定板角点的位置
# 黑白格相交的点我截的图是4*4的
# 准备对象点,如(0,0,0),(1,0,0),(2,0,0)......,(6,5,0)
# objp = np.zeros((w*h,3), np.float32)
objp = np.zeros((4 * 4, 3), np.float32)
# mgrid把列向量[0:cbraw]复制了cbcol列,把行向量[0:cbcol]复制了cbraw行。
# 转置后reshape
objp[:, :2] = np.mgrid[0:4, 0:4].T.reshape(-1, 2) # 将世界坐标系建在标定板上,所有点的Z坐标全部为0,所以只需要赋值x和y
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
images = glob.glob("data/*.jpg")
for fname in images:
img = cv2.imread(fname)
img = cv2.resize(img, None ,fx=0.1, fy=0.1, interpolation= cv2.INTER_CUBIC)#我的图片太大,我缩小了十倍
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
cv2.imshow('gray', gray)
size = gray.shape[::-1]
print(size)
# int cvFindChessboardCorners(const void * image, CvSize pattern_size, CvPoint2D32f * corners,
# int * corner_count = NULL,
# int flags = CV_CALIB_CB_ADAPTIVE_THRESH );
# 参数说明
# Image:输入的棋盘图,必须是8位的灰度或者彩色图像。
# pattern_size:棋盘图中每行和每列角点的个数
# Corners:检测到的角点
# corner_count: 输出,角点的个数。如果不是NULL,函数将检测到的角点的个数存储于此变量。
ret, corners = cv2.findChessboardCorners(gray, (4, 4), None)
print(ret)
# print(corners)
if ret:#如果检测到角点
obj_points.append(objp)
#第二参数上面检测到角点的坐标
# 第三个参数是计算亚像素角点时考虑的区域的大小,大小为NXN;N = (winSize * 2 + 1)。
# 第四个参数作用类似于winSize,但是总是具有较小的范围,通常忽略(即Size(-1, -1))。
corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
#print(corners2)
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
cv2.drawChessboardCorners(img, (4, 4), corners2, ret) # OpenCV的绘制角点的函数
cv2.imshow('img', img)
cv2.waitKey(0)
print(len(img_points))
cv2.destroyAllWindows()
# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
print("ret:", ret)#bool值
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs) # 旋转向量 # 外参数
print("tvecs:\n", tvecs ) # 平移向量 # 外参数
print("-----------------------------------------------------")
for i in range(len(images)):
img = cv2.imread(images[i])
img = cv2.resize(img, None ,fx=0.1, fy=0.1, interpolation= cv2.INTER_CUBIC)
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片(正常重映射之后会删掉一部分图像)
print (newcameramtx)#优化的相机内参
# #也可以使用remap()进行标定
# mapx,mapy = cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)
# dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibration_data/{}.jpg'.format(i), dst1)
print ("dst的大小为:", dst1.shape)
得到的内参数矩阵为:
三、参考资料
1.Python计算机视觉编程 - 第五章 多视图几何 -张正友相机标定法_柴达夫47的博客-CSDN博客
2.OpenCV学习笔记(二十一)——相机的标定_行歌er的博客-CSDN博客_cv2.undistort
3.计算机视觉之三维重建篇(精简版) 北京邮电大学 鲁鹏_哔哩哔哩_bilibili
4.老师的ppt