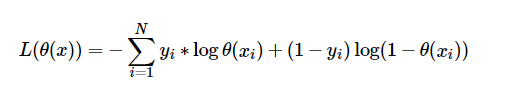激活函数，损失函数，正则化
激活函数简介
在深度学习中，输入值和矩阵的运算是线性的，而多个线性函数的组合仍然是线性函数，对于多个隐藏层的神经网络，如果每一层都是线性函数，那么这些层在做的就只是进行线性计算，最终效果和一个隐藏层相当！那这样的模型的表达能力就非常有限 。
实际上大多数情况下输入数据和输出数据的关系都是非线性的。所以我们通常会用非线性函数对每一层进行激活，大大增加模型可以表达的内容（模型的表达效率和层数有关）。
这时就需要在每一层的后面加上激活函数，为模型提供非线性，使得模型可以表达的形式更多，同时也可以更改模型的输出值，使模型可以实现回归或者分类的功能。常见的激活函数有sigmoid、tanh、relu和softmax。下面分别对其进行介绍。
常见激活函数及优缺点
sigmoid激活函数：
函数公式如下
函数图像如下：
优点：
-
Sigmoid的取值范围在(0, 1)，而且是单调递增，比较容易优化
-
Sigmoid求导比较容易，可以直接推导得出。
缺点：
- Sigmoid函数收敛比较缓慢
- 由于Sigmoid是软饱和，容易产生梯度消失，对于深度网络训练不太适合（从图上sigmoid的导数可以看出当x趋于无穷大的时候，也会使导数趋于0）
- Sigmoid函数并不是以（0,0）为中心点
softmax函数：
公式：
举个例子，通过若干层的计算，在输出层，最后得到的某个训练样本的向量的分数是[ 1, 5, 3 ], 那么概率分别就是：
下图说明，softmax函数是怎么计算的
- 除了用于二分类还可以用于多分类，将各个神经元的输出映射到（0,1空间）
tanH函数：
公式：
函数图像：
双切正切函数，取值范围为[-1,1]，tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好。
-
优点：输出以0为中心，收敛速度比sigmoid函数要快
-
缺点：存在梯度消失问题
relu函数：
ReLu是神经网络中的一个激活函数，其优于tanh和sigmoid函数。
引入relu函数的原因：
- 采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
- 对于深层网络，sigmoid函数反向传播时，很容易就会出现 梯度消失 的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
- ReLu会使一部分神经元的输出为0，这样就造成了 网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。
函数：
f(x)=max(0,x)
函数图像：
-
优点：目前最受欢迎的激活函数，在x<0时，硬饱和，在x>0时，导数为1，所以在x>0时保持梯度不衰减，从而可以缓解梯度消失的问题，能更快收敛，并提供神经网络的稀疏表达能力
-
缺点：随着训练的进行，部分输入或落入硬饱和区，导致无法更新权重，称为‘神经元死亡
损失函数
损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。
损失函数一般分为二分类损失函数、多分类损失函数和回归问题损失函数
二分类损失函数有:0-1损失、hinge损失、LogisticCrossEntropyLoss
多分类损失有:SoftmaxCrossEntropyLoss
回归问题损失函数有：均方差误差或根均方差误差、平均绝对值误差和huber损失函数
0-1损失函数(zero-one loss)
对于二分类问题，Y= {-1,1},我们希望signf(xi,θ)=yi,最自然的损失是0-1损失，即
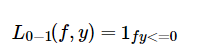
该损失函数能够直观地刻画分类的错误率，但是由于其非凸，非光滑使得算法很难对该函数进行优化，下面将总结0-1损失的二个代理函数：HingeLoss,LogsiticCrossEntropyLoss
HingeLoss
定义
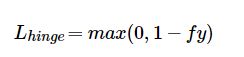Hinge损失函数是0-1损失函数相对紧的凸上界，且当fy >=1时，该函数不对其做任何惩罚，Hinge损失在fy=1处不可导，因此不能用梯度下降法进行优化，而是用次梯度下降法
LogisticCrossEntropyLoss
对数似然函数：
SoftmaxCrossEntropyLoss
损失函数：
均方差
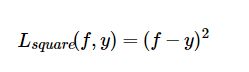
当预测值距离真实值越大时，平方损失函数的惩罚力度越大，因此它对异常点比较敏感，为了解决这个问题，可以使用平均绝对损失函数
平均绝对误差
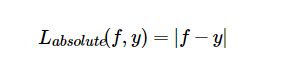
绝对损失函数相当于在做中值回归，相比于做均值回归的平方损失函数对异常点的鲁棒性更好一些，当时有个问题是在f=y时无法求导，综合考虑可导性和对异常点的鲁棒性，采用Huber损失函数
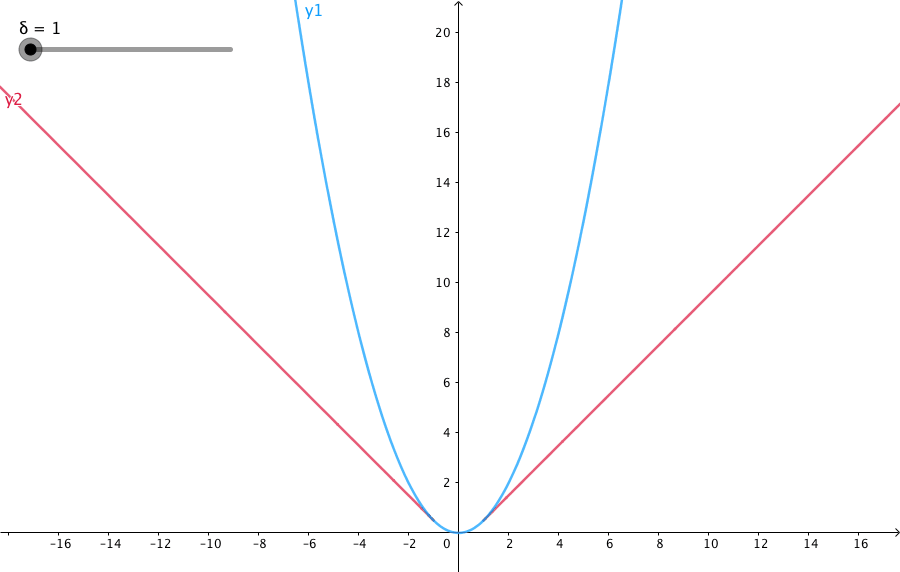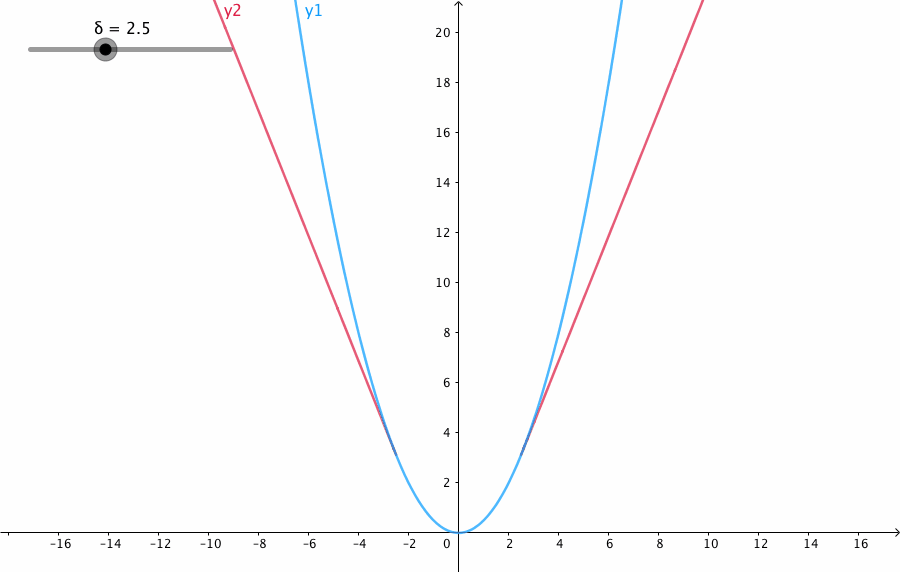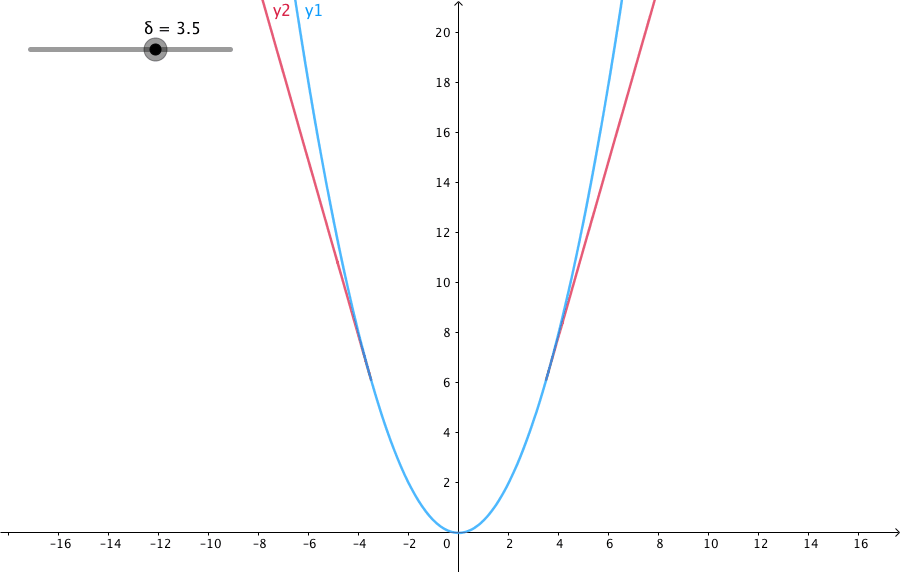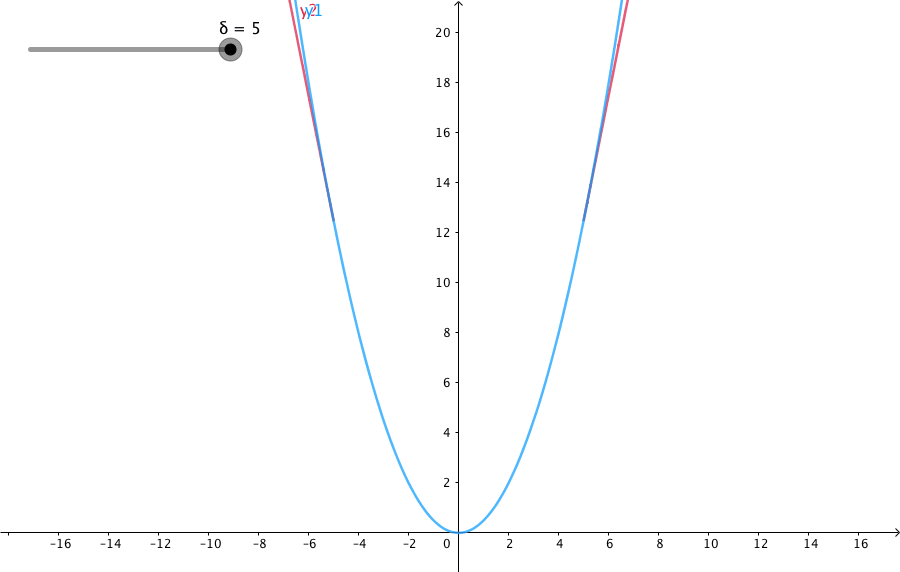
HuberLoss
Huber Loss 是一个用于回归问题的带参损失函数, 优点是能增强平方误差损失函数(MSE, mean square error)对离群点的鲁棒性
当预测偏差小于 δ 时，它采用平方误差
当预测偏差大于 δ 时，采用的线性误差
正则化
正则化(regularization)的技术，它可以改善或者减少过度拟合问题。
欠拟合和过拟合
下图是一个回归问题的例子：
第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。
分类问题中也存在这样的问题：
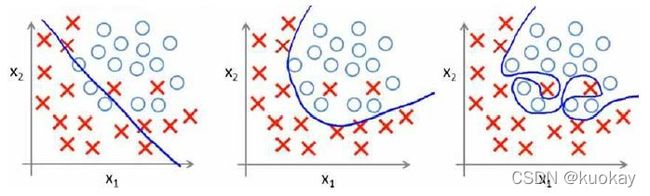
就以多项式理解，x$的次数越高，拟合的越好，但相应的预测的能力就可能变差。
问题是，如果我们发现了过拟合问题，应该如何处理？
-
丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
-
正则化。 保留所有的特征，但是减少参数的大小（magnitude）。
正则化线性回归
对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。
正则化线性回归的代价函数为：
如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对进行正则化，所以梯度下降算法将分两种情形：
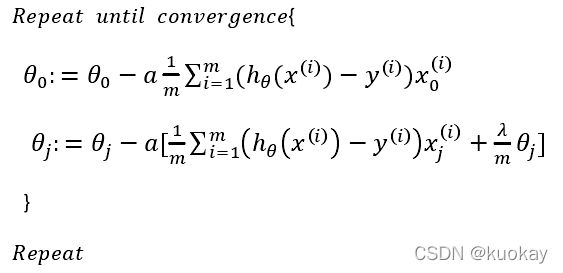
对上面的算法中 = 1,2, . . . , 时的更新式子进行调整可得：
可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：
图中的矩阵尺寸为 (n+1)*(n+1)。
正则化的逻辑回归模型
针对逻辑回归问题，我们在之前的课程已经学习过两种优化算法：我们首先学习了使用梯度下降法来优化代价函数()，接下来学习了更高级的优化算法，这些高级优化算法需要你自己设计代价函数()。
自己计算导数同样对于逻辑回归，我们也给代价函数增加一个正则化的表达式，得到代价函数：
python代码：
import numpy as np
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:the
ta.shape[1]],2))
return np.sum(first - second) / (len(X)) + reg
要最小化该代价函数，通过求导，得出梯度下降算法为：
注：看上去同线性回归一样，但是知道 hθ(x)=g(θTX)，所以与线性回归不同。
Octave 中，我们依旧可以用 fminuc 函数来求解代价函数最小化的参数，值得注意的是参数θ0的更新规则与其他情况不同。 注意：
-
虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样，但由于两者的hθ(x)不同所以还是有很大差别。
-
θ0不参与其中的任何一个正则化。