绘制 混淆矩阵

---

1.混淆矩阵的相关概念

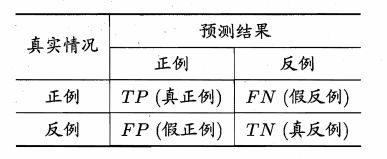
从而二分类的角度来看，在二分类的模型中，把预测情况与实际情况的所有结果进行组合，就会有真正 (true positive)、假正 (false positive)、真负 (true negative) 和假负 (false negative) 四种情形，分别由TP、FP、TN、FN 表示（T代表预测正确，F代表预测错误），这四种情形构成了混淆矩阵。

其实从上图中就可以，只有出现在对角线上的预测结果才是对的，其他的都是错的。
四种情况相加，就是总的样本数。

对于不同的场景，我们对模型的要求也不同

• 对于诊断疾病的模型，模型应该更倾向于找出所有为 反 的样本（患病的患者）；
• 对于垃圾邮件检测模型，该模型应该更倾向于选出所有为 正 的样本（正常邮件）。

2.代码实现：

#confusion_matrix
import numpy as np
import matplotlib.pyplot as plt
# classes = ['A','B','C','D','E']
# confusion_matrix = np.array([(9,1,3,4,0),(2,13,1,3,4),(1,4,10,0,13),(3,1,1,17,0),(0,0,0,1,14)],dtype=np.float64)


# 标签
classes=['angry','disgust','scared','happy','sad','surprised','neutral']

# 标签的个数
classNamber=7 #表情的数量

# 在标签中的矩阵
confusion_matrix = np.array([
    (0.70,0   ,0.07, 0.04, 0.09, 0.01, 0.09),
    (0.18,0.75,0,    0,    0.03, 0.02, 0.02),
    (0.09,0,   0.51, 0.04, 0.17, 0.09, 0.10),
    (0.02,0,   0.01, 0.91, 0.02, 0.01, 0.03),
    (0.10,0,   0.11, 0.03, 0.57, 0.01, 0.17),
    (0.02,0,   0.07, 0.04, 0,    0.84,0),
    (0.04,0,   0.03, 0.07, 0.12, 0.02,  0.72)
    ],dtype=np.float64)

plt.imshow(confusion_matrix, interpolation='nearest', cmap=plt.cm.Oranges)  #按照像素显示出矩阵
plt.title('confusion_matrix')
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=-45)
plt.yticks(tick_marks, classes)

thresh = confusion_matrix.max() / 2.
#iters = [[i,j] for i in range(len(classes)) for j in range((classes))]
#ij配对，遍历矩阵迭代器
iters = np.reshape([[[i,j] for j in range(classNamber)] for i in range(classNamber)],(confusion_matrix.size,2))
for i, j in iters:
    plt.text(j, i, format(confusion_matrix[i, j]),va='center',ha='center')   #显示对应的数字

plt.ylabel('Real label')
plt.xlabel('Prediction')
plt.tight_layout()
plt.show()

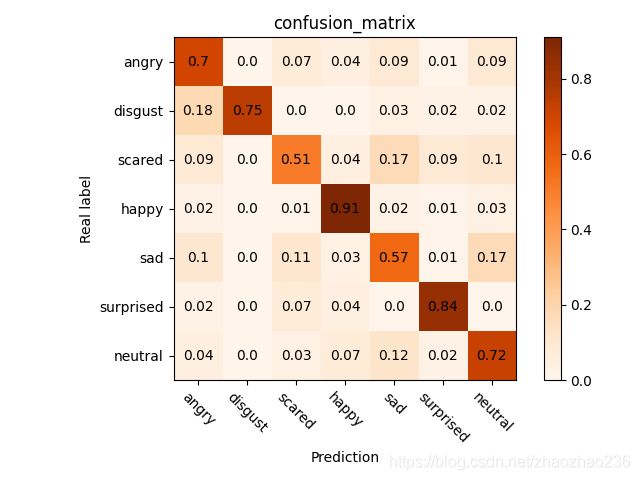
效果图：

参考文献

[1]https://zhuanlan.zhihu.com/p/68473880
[2]https://blog.csdn.net/u014636245/article/details/85628083