统计学三大分布(卡方、t、F)即相应概率密度图的R语言实现
三大统计分布
1. χ 2 \chi^2 χ2分布
设随机变量 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn相互独立且均服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),则称随机变量
χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 \chi^2=X_1^2+X_2^2+\cdots+X_n^2 χ2=X12+X22+⋯+Xn2
所服从的分布是自由度为 n n n的 χ 2 \chi^2 χ2分布,记为 χ 2 ∼ χ 2 ( n ) \chi^2\sim \chi^2(n) χ2∼χ2(n)
χ 2 \chi^2 χ2分布的可加性:设 χ 1 2 ∼ χ 2 ( n 1 ) \chi_1^2\sim \chi^2(n_1) χ12∼χ2(n1), χ 2 2 ∼ χ 2 ( n 2 ) \chi_2^2\sim \chi^2(n_2) χ22∼χ2(n2),且 χ 1 2 \chi_1^2 χ12与 χ 2 2 \chi_2^2 χ22独立,则 χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) \chi_1^2+\chi_2^2\sim \chi^2(n_1+n_2) χ12+χ22∼χ2(n1+n2).
2. t t t分布
设 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1), Y ∼ χ 2 ( n ) Y \sim \chi^2(n) Y∼χ2(n),并且 X X X与 Y Y Y独立,则称随机变量
t = X Y / n t=\frac{X}{\sqrt{Y/n}} t=Y/nX
所服从的分布是自由度为 n n n的 t t t分布,记为 t ∼ t ( n ) t \sim t(n) t∼t(n).
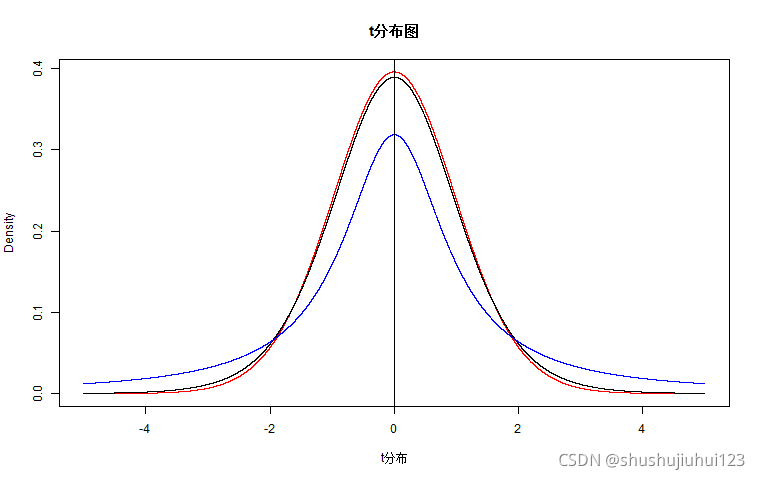
当 n n n充分大时,自由度为 n n n的 t t t分布可近似地看成标准正态分布。当n>30时, t t t分布和标准正态分布就已经非常接近了,但对较小的 n n n, t t t分布与标准正态分布之间有较大的差异,且 t t t分布的尾部比标准正态分布的尾部有着更大的概率,即如果 T ∼ t ( n ) T\sim t(n) T∼t(n), X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1),则对于充分大的正数 t 0 t_0 t0,有
KaTeX parse error: Undefined control sequence: \notag at position 102: …nt t_0\right\} \̲n̲o̲t̲a̲g̲ ̲
在描述不是十分罕见的极端事件所服从的统计规律性时, t t t分布是一个比正态分布更加符合实际的概率分布。
3. F F F分布
设 X ∼ χ 2 ( n 1 ) X \sim \chi^2(n_1) X∼χ2(n1), Y ∼ χ 2 ( n 2 ) Y \sim \chi^2(n_2) Y∼χ2(n2),且 X X X与 Y Y Y独立,则称随机变量
F = X / n 1 Y / n 2 F=\frac{X/n_1}{Y/n_2} F=Y/n2X/n1
所服从的分布是自由度为 ( n 1 , n 2 ) (n_1,n_2) (n1,n2)的 F F F分布,记为 F ∼ F ( n 1 , n 2 ) F \sim F(n_1,n_2) F∼F(n1,n2)
若 F ∼ F ( n 1 , n 2 ) F \sim F(n_1,n_2) F∼F(n1,n2),则 1 F ∼ F ( n 1 , n 2 ) \frac{1}{F}\sim F(n_1,n_2) F1∼F(n1,n2)
绘图的R代码:
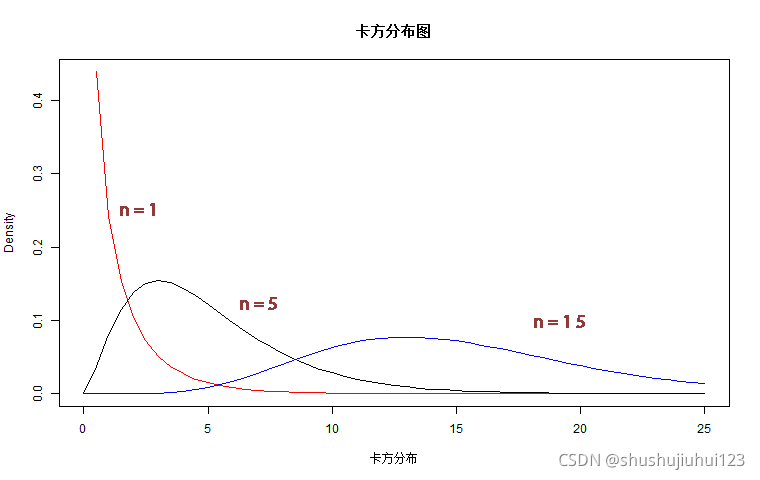
卡方分布概率密度图
x1 <- seq(0,25,0.5)
> y1 <- dchisq(x1,1)
> y2 <- dchisq(x1,5)
> y3 <- dchisq(x1,15)
> png("D:/Rwork/Picture/卡方分布.png",width=760,height = 480)
> plot(x1,y1,xlab="卡方分布",ylab="Density",type="l",col="red",lwd=1.6,main="卡方分布图")
> lines(x1,y2,lwd=1.6,type="l")
> lines(x1,y3,lwd=1.6,type="l",col="blue")
> dev.off()
t分布概率密度图
x1 <- seq(-5,5,0.0001)
> y1 <- dt(x1,1)
> y2 <- dt(x1,10)
> y3 <- dt(x1,30)
> png("D:/Rwork/Picture/t分布.png",width=760,height = 480)
> plot(x1,y3,xlab="t分布",ylab="Density",type="l",col="red",lwd=1.6,main="t分布图")
> lines(x1,y2,lwd=1.6,type="l")
> lines(x1,y1,lwd=1.6,type="l",col="blue")
> abline(v=0)
> dev.off()
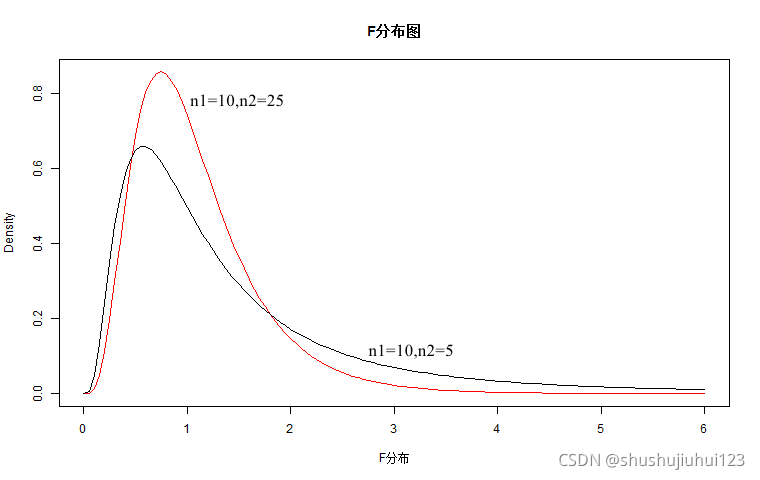
F分布概率密度图
```R
x1 <- seq(0,6,0.05)
y1 <- df(x1,10,25)
y2 <- df(x1,10,5)
png("D:/Rwork/Picture/F分布.png",width=760,height = 480)
plot(x1,y1,xlab="F分布",ylab="Density",type="l",col="red",lwd=1.6,main="F分布图")
lines(x1,y2,lwd=1.6,type="l")
dev.off()