【PyTorch】PyTorch深度学习实践|视频学习笔记|P10-11|CNN
PyTorch深度学习实践|CNN
CNN基础篇
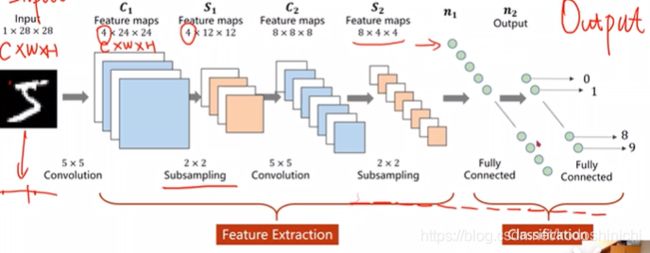
CNN的整体计算框架
①相较全连接网络来说，CNN采用卷积核的层次架构是为了保留输入数据的空间特征信息；
②CNN从本质上来说，就是通过网络的叠加对原始数据做特征提取（Feature Extraction），将原始数据空间映射到目标特征空间，再对映射后得到的特征图，进行向量拉伸，连上一个FC和分类层。
卷积、池化与步长
- convolution（卷积）
考虑最一般的卷积操作，有以下要点和结论：
①卷积核的通道数量应该和输入数据的通道数量保持一致；
②经过卷积运算后数据的通道数量应该和卷积核的个数保持一致；
③在卷积层和卷积运算中，输入图像的长宽和卷积核的大小并不存在对应关系，根据需求进行设定即可
④根据输入出数据的通道需求，假设需要m个大小为n x kernel_sizewidth x kernel_sizeheight的卷积核，则可以把这m个卷积核组合成一个四维张量的形式：m x n x kernel_sizewidth x kernel_sizeheight
import torch
#相关参数设定
in_channels,out_channels = 5,10
width,height = 100,100
kernel_size = 3
batch_size = 1 #在pytorch的实现中，所有数据都要采用mini-batch的形式
#随机化输入数据
input_data = torch.randn(batch_size,in_channels,width,height) #注意数据的维度写法(B,C,W,H)
#构造卷积层
conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size)#注意卷积层模型需传递的参数
#卷积计算输出结果
output_data = conv_layer(input_data)
#以下打印输入出和卷积层参数的维度，体会其中的维度变化
print(input_data.shape)
print(output_data.shape)
print(conv_layer.weight.shape)
'''
运行结果：
torch.Size([1, 5, 100, 100])
torch.Size([1, 10, 98, 98])
torch.Size([10, 5, 3, 3])
'''
- padding（补零）
import torch
input_data = [3,4,6,5,7,
2,4,6,8,2,
1,6,7,8,4,
9,7,4,6,2,
3,7,5,4,1]
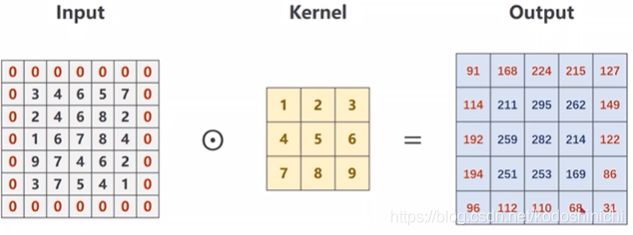
input_data = torch.Tensor(input_data).view(1,1,5,5)#将输入数据变形成（B,C,W,H）的形状
conv_layer = torch.nn.Conv2d(1,1,kernel_size=3,padding=1,bias = False)
kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1,1,3,3)#卷积核应该满足（in_channel,out_channel,k_w,k_h)
conv_layer.weight.data = kernel.data #手动赋予卷积层权值
output_data = conv_layer(input_data)
print(output_data)
'''
运行结果：
tensor([[[[ 91., 168., 224., 215., 127.],
[114., 211., 295., 262., 149.],
[192., 259., 282., 214., 122.],
[194., 251., 253., 169., 86.],
[ 96., 112., 110., 68., 31.]]]],
grad_fn=)
'''
- stride（步长）
- 通过在实例化卷积层对象的时候设置位置参数
stride = xxx来设定该卷积层运算的步长；- 步长改变的是卷积核每次右移（或下移）中心移动的像素点数；
- 不同的stride会使得卷积运算的数据结果的形状发生相应变化。
conv_layer = torch.nn.Conv2d(1,1,kernel_size=3,padding=1,stride=2,bias = False)
- Max_Pooling（最大池化）
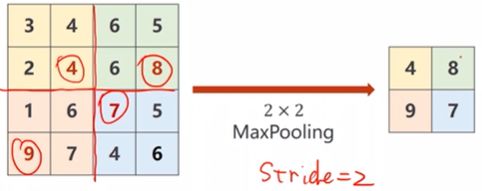
①最大池化层就是在给定的kernel_size x kernel_size的区域中选择当前最大的值作为输出中一个元素值；
②最大池化层没有参数，只需要指定kernel_size的大小即可；
③池化计算过程与通道数无关，因此计算前后数据的通道数也不会发生变化。
import torch
input_data = [3,4,6,5,
2,4,6,8,
1,6,7,8,
9,7,4,6]
input_data = torch.Tensor(input_data).view(1,1,4,4)
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)
output_data = maxpooling_layer(input_data)
print(output_data)
'''
运行结果：
tensor([[[[4., 8.],
[9., 8.]]]])
'''
卷积层模型实例
①卷积-池化-激活或者卷积-激活-池化的顺序都可以，只要激活在两次卷积运算之间进行即可；
②要注意在进行全连接之前，首先将张量拉伸成一维的；
import torch
class Net(torch.nn.Module):
def __init__(self):
super(Net,self).__init__()
self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5)
self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320,10) #这里的参数要计算匹配
def _forward(self,x):
batch_size = x.size(0)
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
#将形如（n,1,28,28）的数据拉伸成（n,784）的形式，batch_size保持不变
x = x.view(batch_size,-1) #进行FC之前将向量拉长
x = self.fc(x) #采用多分类，最后一层不进行激活
return x
model = Net()
GPU模型迁移
- 设定可行的设备参量
device = torch.device("cuda:0" if torch.cuda is available() else "cpu")
- 将模型及其参数进行迁移
model.to(device)
- 将数据集的输入输出进行迁移
如果将训练和测试过程都封装了函数
train()和test()，则在函数内要对数据进行迁移；
否则要在主函数逻辑中的前向计算-反向传播-参数更新的逻辑链中对数据进行迁移。
inputs,targets = inputs.to(device),targets.to(device)
案例
- 使用CNN训练MNIST手写数字识别问题
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import matplotlib.pyplot as plt
#超参数定义
BATCH_SIZE = 512
EPOCHS = 20
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
#准备数据,转换成张量类型的数据，并进行归一化操作
batch_size = 64
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307),(0.3081))
])
train_dataset = datasets.MNIST(root = "../dataset/mnist",
train = True,download=False,transform = transform)
train_loader = DataLoader(train_dataset,shuffle = True,batch_size = batch_size)
test_dataset = datasets.MNIST(root = "../dataset/mnist",train = False,
download=False,transform = transform)
test_loader = DataLoader(test_dataset,shuffle = True,batch_size = batch_size)
#自定义网络模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.conv1 = torch.nn.Conv2d(1,10,kernel_size = 5)
self.conv2 = torch.nn.Conv2d(10,20,kernel_size=3,padding = 1)
self.conv3 = torch.nn.Conv2d(20,20,kernel_size=3,padding = 1)
self.pooling = torch.nn.MaxPool2d(2)
self.l1 = torch.nn.Linear(180,16)
self.l2 = torch.nn.Linear(16,10)
def forward(self, x):
batch_size = x.size(0)
x = self.pooling(F.relu(self.conv1(x)))
x = self.pooling(F.relu(self.conv2(x)))
x = self.pooling(F.relu(self.conv3(x)))
x = x.view(batch_size, -1) # 进行FC之前将向量拉长
x = self.l1(x)
return self.l2(x)
model = Model().to(DEVICE)
#构建损失函数的计算和优化器
criterion = torch.nn.CrossEntropyLoss()#多分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.01)#采用SGD
#训练过程，包括前向计算和反向传播，封装成一个函数
def train(epoch):
running_loss = 0.0
for batch_idx,data in enumerate(train_loader,0):
inputs,target = data
op.zero_grad()
#前向计算
outputs = model(inputs)
loss = criterion(outputs,target)
#反向传播与权值更新
loss.backward()
op.step()
running_loss += loss.item()
if batch_idx % 300 == 299:#每训练300代就输出一次
print('[%d,%5d] loss: %3f' % (epoch+1,batch_idx+1,running_loss / 300))
running_loss = 0.0
#测试过程，封装成函数
def vali():
correct = 0
total = 0
with torch.no_grad():#因为test的过程无需反向传播，也就不需要计算梯度
for data in test_loader:
images,labels = data
outputs = model(images)
_,predicted = torch.max(outputs.data,dim = 1)#因为是按批给的数据
#所以得到的数据标签也是一个矩阵
total += labels.size(0) #同样labels也是一个Nx1的张量
correct += (predicted == labels).sum().item()
print('Accuracy on test set: %d %%'%(100 * correct / total))
#主函数逻辑
if __name__ == '__main__':
for epoch in range(10): #一共训练10epochs
train(epoch)
vali()
'''
运行结果：
[1, 300] loss: 2.224153
[1, 600] loss: 0.954984
[1, 900] loss: 0.318726
Accuracy on test set: 93 %
[2, 300] loss: 0.198788
[2, 600] loss: 0.157404
[2, 900] loss: 0.145021
Accuracy on test set: 96 %
[3, 300] loss: 0.122874
[3, 600] loss: 0.120096
[3, 900] loss: 0.105074
Accuracy on test set: 96 %
[4, 300] loss: 0.094667
[4, 600] loss: 0.095276
[4, 900] loss: 0.090835
Accuracy on test set: 97 %
[5, 300] loss: 0.084520
[5, 600] loss: 0.084876
[5, 900] loss: 0.078178
Accuracy on test set: 97 %
[6, 300] loss: 0.074427
[6, 600] loss: 0.072950
[6, 900] loss: 0.074670
Accuracy on test set: 98 %
[7, 300] loss: 0.067066
[7, 600] loss: 0.068477
[7, 900] loss: 0.066709
Accuracy on test set: 98 %
[8, 300] loss: 0.060533
[8, 600] loss: 0.060498
[8, 900] loss: 0.064969
Accuracy on test set: 98 %
[9, 300] loss: 0.056990
[9, 600] loss: 0.057694
[9, 900] loss: 0.057002
Accuracy on test set: 98 %
[10, 300] loss: 0.056185
[10, 600] loss: 0.056508
[10, 900] loss: 0.050906
Accuracy on test set: 98 %
'''
CNN高级篇
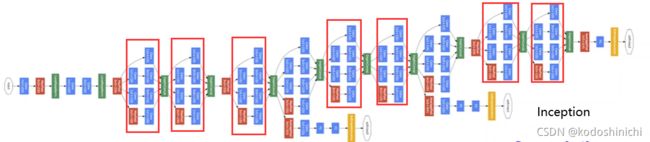
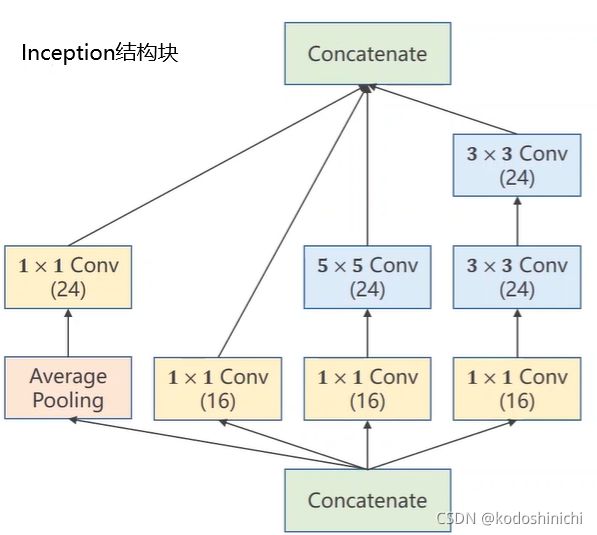
GoogleNet
- 网络结构
可以看到网络结构趋向于复杂，那么我们在定义实现这个网络时，就要尽可能减少代码的冗余：
①面向过程编程中，使用函数进行功能封装
②面向对象编程中，使用类进行功能封装
2. Inception
该网络构成的基本思路：因为事先无法知道超参数怎样选择才能使得网络具有最优的结果，因此对各种可能的超参数结构进行一个罗列，通过训练结果自然可以看出哪种超参数更优。
p.s.其中因为各路分支采取的kernel_size不一致，但是在最终拼接的时候要求图像块的尺寸WXH是一致的，所以需要规定好stride和padding。
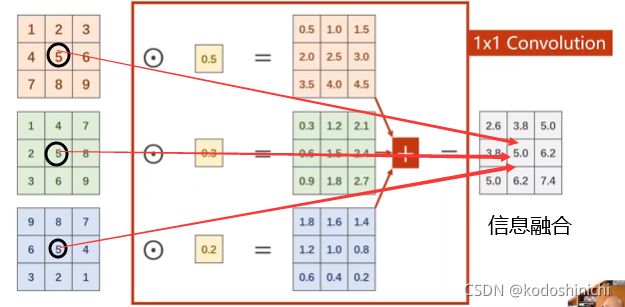
- 1x1卷积
①它可以跨越不同通道的相同位置的元素值，也可以说成是实现了信息融合；
②1x1卷积最直接的作用就是改变数据的通道数目；
③从应用角度来说，1x1卷积的结构可以大大减少计算量。
- 实现
- Inception块各个计算分支的实现
import torch
import torch.nn.functional as F
#对Inception网络块中的各个计算分支进行实现
#以下每个代码块均按照以下逻辑展开：
# 先写类定义中的初始化
# 再写出数据的前向传播计算过程
# Average-Pooling + 1x1 Conv
self.branch_pool = nn.Conv2d(in_channels,24,kernel_size = 1)
branch_pool = F.avg_pool2d(x,kernel_size = 3,stride = 1,padding = 1)#维度一致，使用padding
branch_pool = self.branch_pool(branch_pool)
# 1x1 Conv
self.branch1x1 = nn.Conv2d(in_channels,16,kernel_size = 1)
branch1x1 = self.branch1x1(x)
# 1x1 Conv + 5x5 Conv
self.branch5x5_1 = nn.Conv2d(in_channels,16,kernel_size = 1)
self.branch5x5_2 = nn.Conv2d(16,24,kernel_size = 5,padding = 2)#维度一致，使用padding
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
#1x1 Conv + 3x3 Conv + 3x3 Conv
self.branch3x3_1 = nn.Conv2d(in_channels,16,kernel_size = 1)
self.branch3x3_2 = nn.Conv2d(16,24,kernel_size = 3,padding = 1)
self.branch3x3_3 = nn.Conv2d(24,24,kernel_size = 3,padding = 1)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
- Inception块和含有Inception块的网络结构的代码实现
# 首先对Inception网络块进行抽象封装
# 其他的网络结构则可以直接调用封装好的Incpetion块来构成完整网络
class InceptionA(nn.Module):
def __init__(self,in_channels):
super(InceptionA,self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self,x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x,kernel_size = 3,stride = 1,padding = 1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1,branch5x5,branch3x3,branch_pool]
return torch.cat(outputs,dim = 1)#沿着通道方向进行堆叠
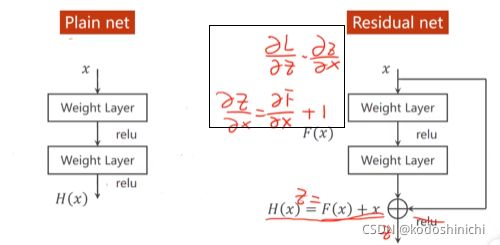
ResNet
- 提出背景
总的来说，ResNet框架的诞生源于深度学习中网络越来越深和训练越来越难之间的一个trade-off：
①一方面，我们希望网络尽可能学习到更加复杂和细粒度的特征；
②另一方面，深层网络在训练之中会碰到梯度消失的问题。
- 基本思想
- skip connection
梯度消失产生的原因：在链式求导法则下，大量小于1的数字连乘最终会趋向于0，使得接近输入层的网络权值无法得到很好的训练。
解决的方法：在进行激活函数之前，这层的输出值先和输入值进行一个叠加，这样在进行梯度求导时，接近于0的梯度就会变成接近于1，连乘时就不再会产生趋近于0的问题。
- 实现
（1）残差网络块的实现
# 残差网络块的实现
class ResidualBlock(nn.Module):
def __init__(self,channels):
super(ResidualBlock,self).__init__()
self.channels = channels
self.conv1 = nn.Conv2d(channels,channels,kernel_size = 3,padding = 1)
self.conv2 = nn.Conv2d(channels,channels,kernel_size = 3,padding = 1)
#因为残差块的输入出最后要叠加起来一起进行激活，所以通道、长和宽这里都处理成一致的
def forward(self,x):
y = F.relu(self.conv1(x))
y = self.conv2(y)
return F.relu(x+y)
（2）残差网络块在整个深度神经网络中的实现
#利用残差块搭建网络结构
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5, padding=2)
self.mp = nn.MaxPool2d(2)
self.rblock1 = ResidualBlock(16)
self.rblock2 = ResidualBlock(32)
self.fc = nn.Linear(512,10)
def forward(self,x):
in_size = x.size(0)
x = self.mp(F.relu(self.conv1(x)))
x = self.rblock1(x)
x = self.mp(F.relu(self.conv2(x)))
x = self.rblock2(x)
x = x.view(in_size,-1)
x = self.fc(x)
return x
遗留问题：我没有计算出为什么线性层的输入维度是512
课后作业
-
多种ResNet的构造方式
-
Densely-connected卷积网络
之后会以paper_reading的形式给出