自监督学习(Self-Supervised Learning)
自监督学习(Self-Supervised Learning)
在神经网络的训练中,良好的性能通常需要大量有标签的数据,但是收集带有手工标签的数据是非常昂贵的(例如ImageNet),并且很难扩大规模。考虑到未标记数据(如免费文本,互联网上的所有图像)的数量远远超过人类管理的标记数据集的数量,不使用它们是一种浪费。然而,无监督学习并不容易,而且效率通常比监督学习低得多。如果我们可以为无标记的数据免费获得标签,并以监督的方式训练无监督的数据集,那会怎么样呢?我们可以通过构建一个特殊形式的监督学习任务来实现这一目标,利用剩余的信息只预测其中的一个子集。这样就提供了所需的所有信息,包括输入和标签。这就是所谓的自我监督学习(Self-Supervised Learning)。
这是我精心挑选的自我监督学习论文清单。 如果您有兴趣进一步阅读,请点击。
文章目录
- 自监督学习(Self-Supervised Learning)
-
- 什么是自监督学习
- 自监督学习的主要方法(基于图像)
-
- 图像失真
- 图像补丁
- 生成模型
- 对比模型(Contrastive Learning )
- 动量对比(Momentum Contrast)
- 讨论
- 参考文献
什么是自监督学习
机器学习一般可分为监督学习,无监督学习,强化学习。自监督学习(Self-Supervised Learning)就是无监督学习里面的一种,也被称作(pretext task),自监督任务(self-supervised task)主要是引导我们学习一个监督损失函数。然而,我们通常并不关心这个任务的最终表现。相反,我们感兴趣的是学习的中间表示,期望这种带有良好的语义或结构意义的表征,可以有益于各种实际的下游任务。例如,我们可能随机旋转图像并训练模型以预测每个输入图像的旋转方式。 旋转预测任务是虚构的,因此实际精度并不重要,就像我们对待辅助任务的方式一样。 但是我们希望该模型能够学习现实任务中的高质量潜在变量,例如构造带有很少标记样本的目标识别分类器。广义上讲,所有生成模型都可以被认为是自我监督的,但目标是不同的:生成模型侧重于创建各种逼真的图像,而自我监督的表示学习则关心产生良好的特征,这些特征通常对许多任务有用。
所以,对自监督学习来说,存在三个挑战:
- 对于大量的无标签数据,如何进行表征学习?
- 从数据的本身出发,如何设计有效的辅助任务 pretext?
- 对于自监督学习到的表征,如何来评测它的有效性?
自监督学习的主要方法(基于图像)
对于图像的自我监督表示学习,已经提出了许多想法。 一种常见的流程是在一个或多个带有未标记图像的自我监督任务上训练模型,然后使用该模型的中间特征层为ImageNet分类提供多项Logistic回归分类器。 最终的分类准确性量化了学习的表征质量。最近,一些研究人员提出了在标注数据上训练有监督学习,同时在无标注数据上训练具有共享权值的自我监督任务,例如Zhai et al,2019和Sun et al,2019。
图像失真
我们期望图像上的微小失真不会改变其原始语义或几何形式。 轻微失真的图像被认为与原始图像语义相同,因此预期学习到的特征不会失真。
Exemplar-CNNDosovitskiy et al., 2015使用无标签的图像补丁来替代训练数据集:
- 从不同位置和比例的不同图像中采样N个大小为32×32像素的色块,仅从包含明显渐变的区域中采样,因为这些区域覆盖边缘并倾向于包含对象或对象的一部分。 它们是“模范”补丁。
- 每个补丁通过应用各种随机变换(例如,平移、旋转、缩放等)而失真。所有由此产生的失真补丁都被认为属于同一个次级类。
- 自监督学习的任务就是区分这些次级类,我们可以产生任何我们想要的数量的次级类。

Fig. 3. 一只可爱的鹿的原始图片位于左上角。 应用随机变换,导致各种失真的补丁。 在自监督任务中,所有这些都应归为同一类。 (图片来源: Dosovitskiy et al., 2015)
RotationGidaris et al. 2018 旋转整个图像是另一种有趣的方法,可在语义内容保持不变的情况下修改输入图像。每个输入图像首先随机旋转90°的倍数,对应于[0 °,90°,180°,270°]。模型经过训练,可以预测应用了哪种旋转,因此产生了4类分类问题。为了识别具有不同旋转度的同一图像,模型必须学会识别物体的高级部分,例如头部,鼻子和眼睛,以及这些部分的相对位置,而不是局部模式。 此前置任务驱动模型以这种方式学习对象的语义概念。
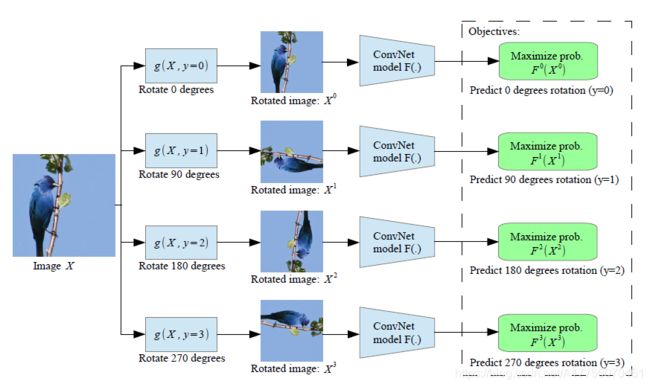
Fig. 4. 通过旋转整个输入图像进行自我监督学习的图示。模型学习预测应用哪个旋转。 (图片来源: Gidaris et al. 2018)
RotationHankook Lee et al. 2020 首先,Data Augmentation相关的方法会对通过对原始图片进行一些变换(颜色、旋转、裁切等)来扩充原始训练集合,提高模型泛化能力;Multi-task learning将正常分类任务和self-supervised learning的任务(比如旋转预测)放到一起进行学习。作者指出通过data augmentation或者multi-task learning等方法的学习强制特征具有一定的不变性,会使得学习更加困难,有可能带来性能降低。因此,作者提出将分类任务的类别和self-supervised learning的类别组合成更多类别(例如 (Cat, 0),(Cat,90)等),用一个损失函数进行学习。
L ( x , y ; θ , w , u ) = L S D A ( x , y ; θ , w ) + D K L ( P a g g r e g a t e d ( ⋅ ∣ x ) ∣ ∣ σ ( f ( x ; θ ) ; u ) ) + β L C E ( σ ( f ( x ; θ ) ; u ) , y ) \Large L(x,y;\theta,w,u)=L_{SDA}(x,y;\theta,w)+D_{KL}(P_{aggregated}(\cdot|x)||\sigma(f(x;\theta);u))+\beta L_{CE}(\sigma(f(x;\theta);u),y) L(x,y;θ,w,u)=LSDA(x,y;θ,w)+DKL(Paggregated(⋅∣x)∣∣σ(f(x;θ);u))+βLCE(σ(f(x;θ);u),y)
其中,第一项和第二项分别对应图(a)和图(b),第三项是正常的交叉熵损失,作为一个辅助 l o s s loss loss
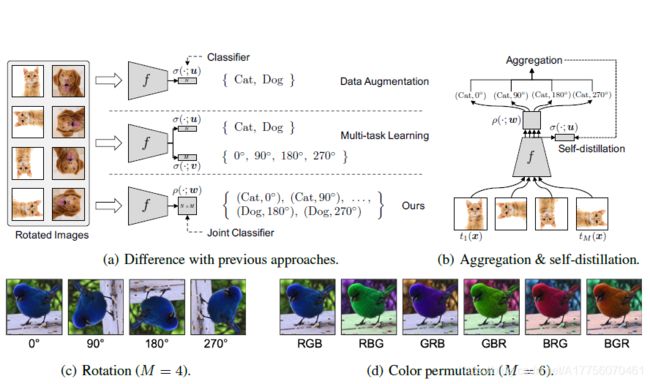
Gidaris, Spyros et al. 2019在小样本学习中探索了在多任务学习中增加自监督学习的可能,他们将普通的分类任务中嵌入了==旋转预测任务==。除了简单的多任务学习,也可以设计联合学习策略,直接预测两种监督信息。一个分支进行传统的小样本分类,另一个分支来进行自监督旋转预测。而自监督和半监督学习Xiaohua Zhai et al. 2019也可以进行结合,和对于有标记数据,在进行自监督学习的同时利用联合训练的想法进行有监督学习。通过对 imagenet 的半监督划分,利用 10% 或者 1% 的数据进行实验,最后分析了一些超参数对于最终性能的影响。
图像补丁
第二类自我监督学习任务从一张图像中提取多个补丁,并要求模型预测这些补丁之间的关系。
Doersch et al. (2015)将自监督任务表述为从一张图像中预测两个随机色块之间的相对位置。 一个模型需要了解对象的空间环境,以便分辨零件之间的==相对位置==。
培训补丁的采样方式如下:
- 在不参考图像内容的情况下随机采样第一个补丁。
- 考虑到第一个补丁被放置在一个3x3网格的中间,第二个补丁从它周围的8个邻近的位置取样。
- 为了避免模型仅捕获低电平的简单信号,例如跨边界连接直线或匹配局部模式,通过以下方式引入额外的噪声:在补丁之间添加间隙;小抖动;随机地对某些补丁进行下采样,使其总像素达到100,然后再对其进行上采样,以建立对像素化的鲁棒性;将绿色和品红移向灰色,或者从3个颜色通道中随机去掉2个(见下面的“色差”)
- 该模型通过训练来预测第二个补丁选自8个邻近点中的哪一个,这是一个8类分类问题。
Fig. 6.通过预测两个随机斑块的相对位置来说明自监督学习。 (图片来源: Doersch et al., 2015)
既然我们在上面的任务中已经在每个图像中设置了3x3的网格,为什么不使用所有的9个补丁而不是仅仅使用2个来增加任务的难度呢? Noroozi & Favaro (2016) 基于这一理念,设计了一款作为自监督任务的==拼图游戏==:训练模型将9个打乱的补丁放回原来的位置。卷积网络使用共享权值独立地处理每个补丁,并从预定义的排列集合中输出每个补丁索引的概率向量。为了控制拼图游戏的难度,本文提出了根据一个预定义的排列集合来洗牌,并配置了该模型来预测集合中所有指标的概率向量。因为输入补丁的混合方式不会改变预测的正确顺序。使用置换不变图卷积网络(GCN)可以避免对同一组补丁进行多次洗牌,从而提高训练速度。

Fig. 7.通过解决拼图游戏的自我监督学习示意图. (图片来源: Noroozi & Favaro, 2016)
另一个想法是将“特征”或“视觉基元”视为一个标量值属性,可以对多个补丁进行汇总,并在不同补丁之间进行比较。 然后可以通过==计算特征==和简单的算术来定义补丁之间的关系 (Noroozi, et al, 2017).
本文考虑了两种转变:
- 缩放:如果图像被放大2倍,视觉基元的数量应该保持不变。
- 平铺:如果将图像平铺成2x2的网格,视觉基元的数量将是原始特征数的4倍。
该模型利用上述特征之间的计数关系学习一种特征编码器 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)。给定一张输入图像 x ∈ R 3 × m × n \mathbf{x}\in\mathbb{R^{3×m×n}} x∈R3×m×n,考虑以下两种类型的转换算子:
- 下采样算子, D : R 3 × m × n ↦ R 3 × m 2 × n 2 D:\mathbb{R}^{3×m×n} \mapsto \mathbb {R}^{3×\frac{m}{2} × \frac{n}{2}} D:R3×m×n↦R3×2m×2n,下取样倍数为2。
- 平铺算子,$T_{i}:\mathbb{R}^{3×m×n} \mapsto \mathbb {R}^{3×\frac{m}{2} × \frac{n}{2}} $,从图像的2x2网格中提取第i个平铺。
我们希望学习得到:
ϕ ( x ) = ϕ ( D ∘ x ) = ∑ i = 1 4 ϕ ( T i ∘ x ) \Large \phi(\mathbf{x})=\phi(D\circ\mathbf{x})=\sum_{i=1}^{4}\phi(T_i\circ\mathbf{x}) ϕ(x)=ϕ(D∘x)=i=1∑4ϕ(Ti∘x)
因此, L f e a t = ∥ ϕ ( D ∘ x ) − ∑ i = 1 4 ϕ ( T i ∘ x ) ∥ 2 2 \mathcal{L}_{feat}=\left \| \phi(D\circ\mathbf{x})- \sum_{i=1}^{4}\phi(T_i\circ\mathbf{x})\right \|_2^2 Lfeat=∥∥∥ϕ(D∘x)−∑i=14ϕ(Ti∘x)∥∥∥22。为了避免平凡解: ∀ x \forall\mathbf{x} ∀x, ϕ ( x ) = 0 \phi(\mathbf{x}) = 0 ϕ(x)=0。另一个损失项是为了鼓励两个不同的图像特征之间的差异 L d i f f = max ( 0 , c − ∥ ϕ ( D ∘ y ) − ∑ i = 1 4 ϕ ( T i ∘ x ) ∥ 2 2 ) \mathcal{L}_{diff}=\max(0,c-\left \| \phi(D\circ\mathbf{y})- \sum_{i=1}^{4}\phi(T_i\circ\mathbf{x})\right \|_2^2) Ldiff=max(0,c−∥∥∥ϕ(D∘y)−∑i=14ϕ(Ti∘x)∥∥∥22),其中 y \mathbf{y} y是另一个不同于 x \mathbf{x} x的输入图片, c c c是一个常量,最终的损失函数为:
L = L f e a t + L d i f f = ∥ ϕ ( D ∘ x ) − ∑ i = 1 4 ϕ ( T i ∘ x ) ∥ 2 2 + max ( 0 , M − ∥ ϕ ( D ∘ y ) − ∑ i = 1 4 ϕ ( T i ∘ x ) ∥ 2 2 ) \Large \mathcal{L}=\mathcal{L}_{feat}+\mathcal{L}_{diff} = \left \| \phi(D\circ\mathbf{x})- \sum_{i=1}^{4}\phi(T_i\circ\mathbf{x})\right \|_2^2+ \max(0,M-\left \| \phi(D\circ\mathbf{y})- \sum_{i=1}^{4}\phi(T_i\circ\mathbf{x})\right \|_2^2) L=Lfeat+Ldiff=∥∥∥∥∥∥∥ϕ(D∘x)−i=1∑4ϕ(Ti∘x)∥∥∥∥∥∥∥22+max(0,M−∥∥∥∥∥∥∥ϕ(D∘y)−i=1∑4ϕ(Ti∘x)∥∥∥∥∥∥∥22)
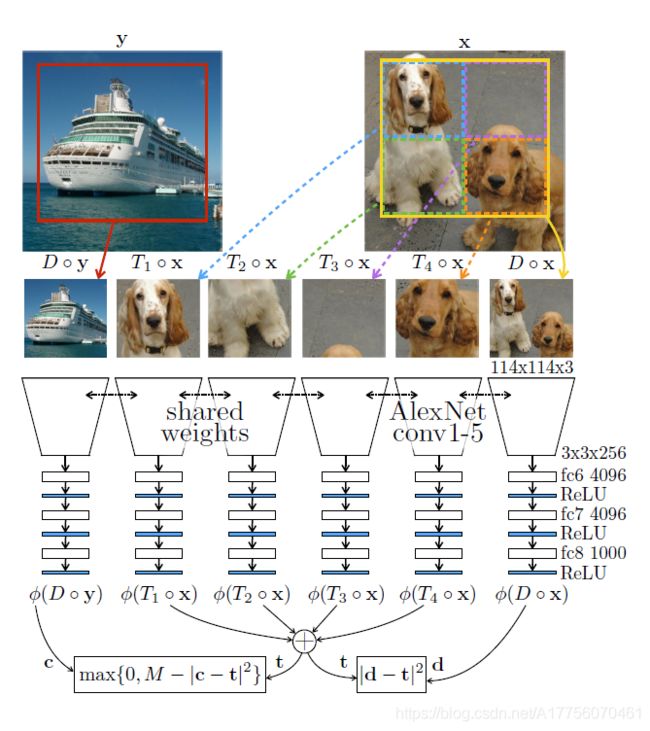
Fig. 7. 基于特征计数的自监督表征学习. (图片来源: Noroozi, et al, 2017)
生成模型
生成模型的自监督任务是在学习有意义的潜在表征的同时重构原始输入。
上下文编码器(context encoder) (Pathak, et al., 2016) 被训练来填补图像中缺失的部分。设 M ^ \hat{M} M^是一个二进制掩码,0表示被丢弃的像素,1表示剩余的输入像素。该模型的训练结合了重建( L 2 L_2 L2)损失和对抗性损失。由掩码定义的被移除的区域可以是任何形状。
KaTeX parse error: No such environment: align at position 15: \Large \begin{̲a̲l̲i̲g̲n̲}̲ \mathcal{L}(\m…
其中, E ( ⋅ ) E(\cdot) E(⋅)是编码器, D ( ⋅ ) D(\cdot) D(⋅)是解码器。

Fig. 8. 基于上下文的编码器图示 (图片来源: Pathak, et al., 2016)
当对图像应用掩码时,上下文编码器删除部分区域中所有颜色信道的信息。那如果只隐藏一部分信道如何?split-brain autoencoder (Zhang et al., 2017)自动编码器通过从剩余信道中预测隐藏的颜色信道的子集来实现这一点。令数据张量 x ∈ R ∣ C ∣ × h × w \mathbb{x} \in \mathbb{R}^{|C|×h×w} x∈R∣C∣×h×w,具有 C C C个颜色信道,作为网络第 l l l层的输入。 x \mathbb{x} x被分为两部分, x 1 ∈ R ∣ C 1 ∣ × h × w \mathbb{x}_1\in\mathbb{R}^{|C_1|×h×w} x1∈R∣C1∣×h×w和 x 2 ∈ R ∣ C 2 ∣ × h × w \mathbb{x}_2\in\mathbb{R}^{|C_2|×h×w} x2∈R∣C2∣×h×w,其中 C 1 , C 2 ∈ C C_1,C_2\in C C1,C2∈C。然后训练两个子网进行两个互补的预测:一个网络 f 1 f_1 f1从 x 1 \mathbb{x_1} x1预测 x 2 \mathbb{x_2} x2,另一个网络 f 2 f_2 f2从 x 2 \mathbb{x_2} x2预测 x 1 \mathbb{x_1} x1。 如果对颜色值进行量化,则损失函数为 L 1 \mathcal{L_1} L1损失函数或交叉熵函数。
这种分裂可以在RGB-D或Lab*颜色空间上发生一次,甚至可以发生在CNN网络的每一层中,其中信道的数量可以是任意的。
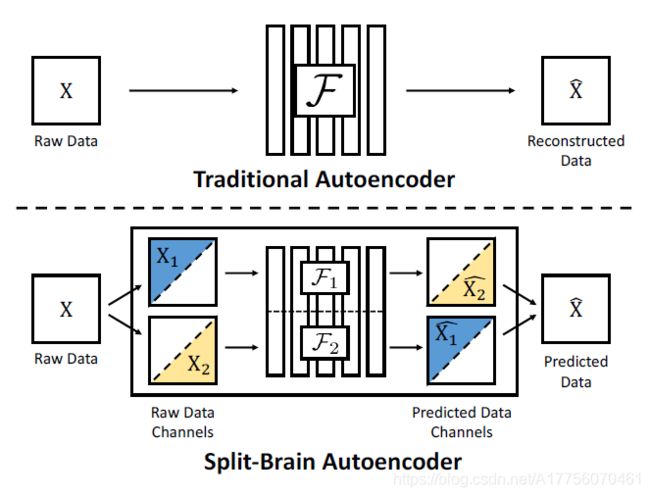
Fig. 9. split-brain 自动编码器的图例. (图片来源: Zhang et al., 2017)
生成对抗网络(generative adversarial networks (GANs))能够学习从简单的潜在变量到任意复杂的数据分布的映射。 研究表明,此类生成模型的潜在空间捕获了数据中的语义变化; 例如 在人脸上训练GAN模型时,一些潜在变量与面部表情,眼镜,性别等相关(Radford et al., 2016)。
双向GANs (Donahue, et al, 2017) 引入了额外的编码器 E ( ⋅ ) E(\cdot) E(⋅)来学习从输入 x \mathbb{x} x到隐变量 z \mathbb{z} z的映射。判别器 D ( ⋅ ) D(\cdot) D(⋅)在输入数据和隐式表示的联合空间 ( x , z ) (\mathbb{x},\mathbb{z}) (x,z)中预测,将生成对 ( x , E ( x ) ) (\mathbb{x},E(\mathbb{x})) (x,E(x))与实对 ( G ( z ) , z ) (G(\mathbb{z}),\mathbb{z}) (G(z),z)区分开。该模型以最小化G,E,最大化 D D D为优化目标 V ( D , E , G ) V(D,E,G) V(D,E,G),其中,生成器 G G G和编码器 E E E学习生成足够真实的数据和隐变量以混淆鉴别器 D D D,同时鉴别器 D D D尝试区分真实数据和生成的数据。

Fig. 10. 双向GANs工作原理图例. (图片来源: Donahue, et al, 2017)
对比模型(Contrastive Learning )
对比模型的自我监督任务是通过学习编码使两个相似或者不同的事物来构建表征。它们不同于更传统的生成式学习表征方法,后者侧重于在像素空间重建误差来学习表征。
- 使用像素级的损失可能会导致这种方法过分关注基于像素的细节,而不是更抽象的潜在因素。
- 基于像素的目标通常假定每个像素之间是独立的,因此降低了它们对相关性或复杂结构建模的能力。
对比预测编码(CPC)(van den Oord, et al. 2018) 是一种通过将生成建模问题转化为分类问题,从而在高维数据进行无监督学习的方法。 可以应用于任何形式的数据,这些数据可以以有序的顺序表示: 文本、语音、视频,甚至图像(图像可以看作是一系列像素或补丁)。CPC 通过编码信息来学习表征,这些信息在多个时间步骤之间共享,而丢弃本地信息。这些特性通常被称为“慢特性”: 这些特性不会随着时间的推移而变化得太快。例如,音频信号中的说话者身份、视频中的活动、图像中的对象等等。在噪声对比估计(NCE)的启发下,CPC中的对比损失或者说是InfoNCE损失使用交叉熵损失来衡量模型在一组不相关的“负”样本中对“未来”表征的分类能力。 设计这种损失的部分动机是因为像MSE这样的单峰损失没有足够的容量,但是学习一个完整的生成模型可能代价过大。
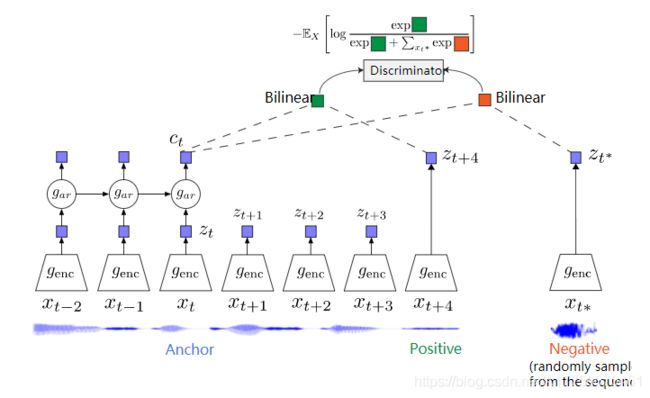
Fig. 11. 对比预测编码在音频输入上的应用示例. (图片来源: van den Oord, et al. 2018)
CPC使用一个编码器来压缩输入数据 z t = g e n c ( x t ) z_t=g_{enc}(x_t) zt=genc(xt),使用一个自回归解码器来学习在未来预测中可能共享的高级上下文, c t = g a r ( z ≤ t ) c_t=g_{ar}(z\leq t) ct=gar(z≤t),端到端的训练依赖于对比损失。在预测未来信息的同时,CPC进行优化,使得输入 x \mathbb{x} x与上下文向量 c \mathbb{c} c之间的互信息最大化:
I ( x ; c ) = ∑ x , c p ( x , c ) log p ( x , c ) p ( x ) p ( c ) = ∑ x , c p ( x , c ) log p ( x ∣ c ) p ( x ) \Large I(\mathbb{x};\mathbb{c})=\sum_{\mathbb{x},\mathbb{c}}p(\mathbb{x},\mathbb{c})\log \frac{p(\mathbb{x},\mathbb{c})}{p(\mathbb{x})p(\mathbb{c})}=\sum_{\mathbb{x},\mathbb{c}}p(\mathbb{x},\mathbb{c})\log \frac{p(\mathbb{x}|\mathbb{c})}{p(\mathbb{x})} I(x;c)=x,c∑p(x,c)logp(x)p(c)p(x,c)=x,c∑p(x,c)logp(x)p(x∣c)
CPC不是对未来观测值 p k ( x t + k ∣ c t ) p_k(x_{t+k}|c_t) pk(xt+k∣ct)建模,而是对密度函数进行建模以保留 x t + k x_{t+k} xt+k和 c t c_t ct之间的互信息:
f k ( x t + k , c t ) = exp ( z t + k T W k c t ) ∝ p ( x ∣ c ) p ( x ) \Large f_k(\mathbb{x}_{t+k},\mathbb{c}_t)=\exp(\mathbb{z}_{t+k}^T W_k \mathbb{c}_t)\propto \frac{p(\mathbb{x}|\mathbb{c})}{p(\mathbb{x})} fk(xt+k,ct)=exp(zt+kTWkct)∝p(x)p(x∣c)
其中 f k f_k fk可以是非归一化的,使用线性变化 W k T c t W_k^T c_t WkTct进行预测,每步 k k k使用不同的矩阵 W k W_k Wk。
给定一组 N N N个随机样本 X = { x 1 , . . . , x N } X = \left\{ \mathbb{x}_1,...,\mathbb{x}_N \right\} X={x1,...,xN},其中仅包含一个正样本 x t ∼ p ( x t + k ∣ c t ) \mathbb{x}_t \sim p(\mathbb{x}_{t+k}|\mathbb{c}_t) xt∼p(xt+k∣ct)和 N − 1 N-1 N−1个负样本 x i ≠ t ∼ p ( x t + k ) \mathbb{x}_{i \neq t}\sim p(\mathbb{x}_{t+k}) xi=t∼p(xt+k),用于对正样本进行分类的交叉熵损失为(其中 f k ∑ f k \frac{f_k}{\sum f_k} ∑fkfk为预测值):
L N = − E X [ log f k ( x t + k , c t ) ∑ i = 1 N f k ( x i , c t ) ] \Large \mathcal{L}_N=-\mathbb{E}_{X}[\log \frac{f_k(x_{t+k},c_t)}{\sum_{i=1}^{N}f_k(\mathbb{x}_i,c_t)}] LN=−EX[log∑i=1Nfk(xi,ct)fk(xt+k,ct)]

Fig. 12. 对比预测编码在图像上的应用示例. (图片来源: van den Oord, et al. 2018)
当在图像上使用CPC时(Henaff, et al. 2019),预测器网络应该只访问被屏蔽的特征集,以避免错误预测,准确的说:
- 每个输入图像被划分为一组重叠的patch,每个patch被resnet编码器编码,得到压缩的特征向量 z i , j z_{i,j} zi,j。
- 一个masked卷积神经网络使用mask进行预测,使得给定输出神经元的接受域只能看到图像中它上方的事物。否则,预测问题将是错误的,预测可以在两个方向上进行(自顶而上和自下而上)
- 根据上下文 c i , j c_{i,j} ci,j对 z i + k , j z_{i+k,j} zi+k,j进行预测: z ^ i + k , j = W k c i , j \hat{z}_{i+k,j}=W_kc_{i,j} z^i+k,j=Wkci,j
对比损失量化了这种预测,其目标是在一组负表征 z l z_l zl中正确地识别目标,这些负表征 z l z_l zl来自同一幅图像中的其他patch,以及同一批图像中的其他图像:
L C P C = − ∑ i , j , k log p ( z i + k , j ∣ z ^ i + k , j , { z l } ) = − ∑ i , j , k log exp ( z ^ i + k , j T z ^ i + k , j ) exp ( z ^ i + k , j T z ^ i + k , j ) + ∑ l exp ( z ^ i + k , j T z l ) \Large \mathcal{L}_{CPC}=-\sum_{i,j,k}\log p(z_{i+k,j}|\hat{z}_{i+k,j},\left\{ z_l\right\})=-\sum_{i,j,k}\log \frac{\exp (\hat{z}_{i+k,j}^T\hat{z}_{i+k,j})}{\exp(\hat{z}_{i+k,j}^T\hat{z}_{i+k,j})+\sum_{l}\exp(\hat{z}_{i+k,j}^Tz_l)} LCPC=−i,j,k∑logp(zi+k,j∣z^i+k,j,{zl})=−i,j,k∑logexp(z^i+k,jTz^i+k,j)+∑lexp(z^i+k,jTzl)exp(z^i+k,jTz^i+k,j)
动量对比(Momentum Contrast)
==动量对比==提供了一个无监督学习的框架,视觉表征作为一个动态字典查找。字典结构是一个大的FIFO队列,对数据样本进行编码表示。
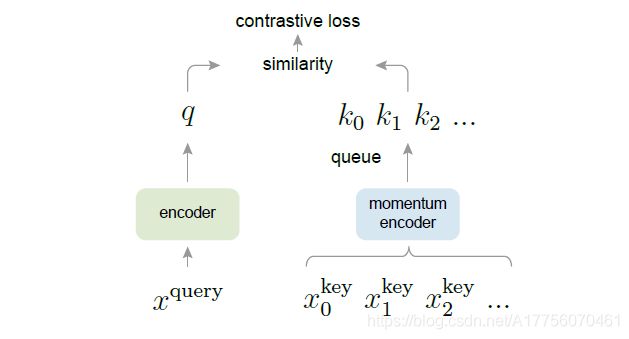
Fig. 13. 动量对比(MoCo)如何学习视觉表征的示意图。 (图片来源: He et al, 2019)
给定查询样本 x q x_q xq,我们通过编码器 f q : q = f q ( x q ) f_q:q=f_q(x_q) fq:q=fq(xq)获得查询表征 q q q。键样本由动量编码器 k i = f k ( x i k ) k_i =f_k(x_i^k) ki=fk(xik)编码,以生成字典中的键表征形式的列表 { k 1 , k 2 , . . . } \left\{k_1,k_2,... \right\} {k1,k2,...}。 让我们假设其中有一个与 q q q匹配的单个正键 k + k+ k+。 在本文中,使用利用不同的数据增强方式获得的的 x q x_q xq的副本创建 k + k+ k+。 然后将InfoNCE对比损失应用于一个正样本和 K K K个负样本:
L q = − log exp ( q ⋅ k + / τ ) ∑ i = 0 K exp ( q ⋅ k i / τ ) \Large \mathcal{L}_q = -\log\frac{\exp(q\cdot k^+/ \tau)}{\sum_{i=0}^K\exp(q \cdot k_i/ \tau)} Lq=−log∑i=0Kexp(q⋅ki/τ)exp(q⋅k+/τ)
其中 τ \tau τ是温度超参数。
与另一个类似的存储库想法(Wu et al, 2018) 相比,该存储库将所有数据点的表征存储在数据库中并随机采样一组键作为负样本,MoCo中基于队列的字典使我们能够重用紧接在前的少量数据。由于基于队列的字典大小,使用反向传播更新键编码器 f q f_q fq很难。 一种简单的方法可能是对 f q f_q fq和 f k f_k fk使用相同的编码器。 不同的是,MoCo建议采用基于动量的更新方式。 假设 f q f_q fq和 f k f_k fk的参数分别记为 θ q \theta_q θq和 θ k \theta_k θk:
θ k ← m θ k + ( 1 − m ) θ q \Large \theta_k \leftarrow m\theta_k+(1-m)\theta_q θk←mθk+(1−m)θq
其中 m ∈ [ 0 , 1 ) m\in[0,1) m∈[0,1)是动量系数, f k f_k fk的更新没有梯度。

Fig. 14. PyTorch风格的MoCo伪代码. (图片来源: He et al, 2019)
SimCLR (Chen et al, 2020)提出了一个简单的框架,用于视觉表示的对比学习。 它通过潜在空间中的对比损失来最大化同一样本的不同增强样本之间的一致性,从而学习视觉输入的表征形式。
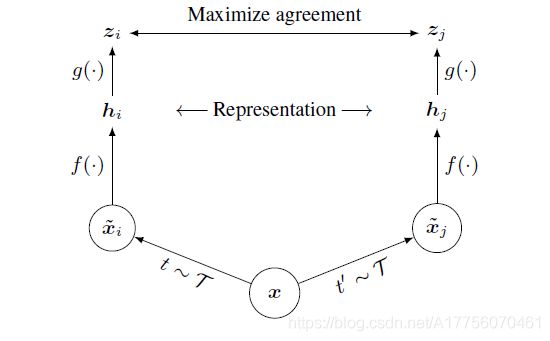
Fig. 15. 一个用于视觉表征的对比学习的简单框架. (图片来源: Chen et al, 2020)
SimCLR的工作分为以下三个步骤:
(1)随机采样小批量n个样本,然后对每个样本应用两次不同的数据增强操作,总共产生2n个增强样本。
x ~ i = t ( x ) , x ~ j = t ′ ( x ) , t , t ′ ∼ τ \Large \tilde{\mathbb{x}}_i=t(\mathbb{x}),\tilde{\mathbb{x}}_j=t^{'}(\mathbb{x}), t,t^{'}\sim \tau x~i=t(x),x~j=t′(x),t,t′∼τ
其中,其中两个独立的数据增强算子 t t t和 t ′ t^{'} t′从相同的增强族 τ \tau τ中采样。 数据增强包括随机裁剪,随机翻转调整大小,颜色失真和高斯模糊。
(2)给定一个正样本,另外2n-1个数据被视为负样本,由编码器 f ( ⋅ ) f(\cdot) f(⋅)产生:
h i = f ( x ~ i ) , h j = f ( x ~ j ) \Large \mathbb{h}_i=f(\tilde{\mathbb{x}}_i), \mathbb{h}_j=f(\tilde{\mathbb{x}}_j) hi=f(x~i),hj=f(x~j)
使用余弦相似度 s i m ( . , . ) sim(.,.) sim(.,.)定义对比损失。 值得注意的是,损失是通过 g ( ⋅ ) g(\cdot) g(⋅)在表征的投影之上进行的,而不是直接在表征 h \mathbb{h} h上进行。 但是只有表征 h \mathbb{h} h用于下游任务。
KaTeX parse error: No such environment: align at position 15: \Large \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{z}_i &…
其中 1 [ k ≠ i ] \mathbf{1}_{[k\neq i]} 1[k=i]是一个one_hot函数。 τ \tau τ是一个温度超参。

Fig. 16. SimCLR算法. (图片来源: Chen et al, 2020).
MoCo与SimCLR相比的优势在于MoCo使batch大小与负样本数量解耦,但是SimCLR需要较大的batch(4096)才能拥有足够的负样本。 因此,当SimCLR的批量大小减小时,性能将下降。
BYOL (“Bootstrap your own latent”; Grill, et al 2020) 称不使用负样本就可以获得新的最先进的结果。它依赖于两个相互交互和学习的神经网络,称为在线和目标网络。 目标网络(由ξ参数化)与在线网络(由θ参数化)具有相同的架构,但具有polyak平均权重 ξ ← τ ξ + ( 1 − τ ) θ \xi\leftarrow \tauξ+(1-\tau)\theta ξ←τξ+(1−τ)θ。目标是学习可以在下游任务中使用的表征y。 在线网络的θ参数化包含:
- 编码器 f θ f_{\theta} fθ
- 投影器 g θ g_{\theta} gθ
- 预测器 q θ q_{\theta} qθ
目标网络具有相同的网络结构,但具有不同的 ξ 参数,用polyak平均法进行更新: ξ ← τ ξ + ( 1 − τ ) θ \xi\leftarrow \tauξ+(1-\tau)\theta ξ←τξ+(1−τ)θ

Fig. 17. BYOL的模型架构 (“Bootstrapping your own latent”). (图片来源: Grill, et al 2020).
给定一个输入图片x,BYOL的损失函数构造如下:
- 创建两个增强样本, v = t ( x ) ; v ′ = t ′ ( x ) v=t(x);v^{'}=t^{'}(x) v=t(x);v′=t′(x),其中增强类型取样自 t ∼ τ , t ′ ∼ τ ′ t\sim\tau,t^{'}\sim\tau^{'} t∼τ,t′∼τ′
- 将他们编码成表征形式: y θ = f θ ( v ) , y ′ = f ξ ( v ′ ) y_{\theta}=f_{\theta}(v),y^{'}=f_{\xi}(v^{'}) yθ=fθ(v),y′=fξ(v′);
- 将他们投影到隐空间: z θ = g θ ( y θ ) , z ′ = g ξ ( v ′ ) z_{\theta}=g_{\theta}(y_{\theta}),z^{'}=g_{\xi}(v^{'}) zθ=gθ(yθ),z′=gξ(v′);
- 在线网络输出预测: q θ ( z θ ) q_{\theta}(z_{\theta}) qθ(zθ);
- 其中 q θ ( z θ ) q_{\theta}(z_{\theta}) qθ(zθ)和 z ′ z^{'} z′都是L2-归一化,得到 q ˉ θ ( z θ ) = q θ ( z θ ) / ∥ q θ ( z θ ) ∥ \bar{q}_{\theta}(z_{\theta})=q_{\theta}(z_{\theta})/ \left \| q_{\theta}(z_{\theta}) \right \| qˉθ(zθ)=qθ(zθ)/∥qθ(zθ)∥和 z ′ ˉ = z ′ / ∥ z ′ ∥ \bar{z^{'}}=z^{'}/ \left \| z^{'} \right \| z′ˉ=z′/∥∥∥z′∥∥∥;
- L θ B Y O L \mathcal{L}_{\theta}^{BYOL} LθBYOL是 q θ ( z θ ) q_{\theta}(z_{\theta}) qθ(zθ)和 z ′ z^{'} z′之间的MSE损失;
- 通过将 v v v替换成 v ˉ \bar{v} vˉ得到另一个对称式损失 L ˉ θ B Y O L \bar{\mathcal{L}}_{\theta}^{BYOL} LˉθBYOL
- 最终的损失函数为 L θ B Y O L \mathcal{L}_{\theta}^{BYOL} LθBYOL+ L ˉ θ B Y O L \bar{\mathcal{L}}_{\theta}^{BYOL} LˉθBYOL,并且只更新参数 θ \theta θ
与大多数流行的基于对比学习的方法不同,BYOL 不使用负样本。大多数方法依赖于伪标签或集群索引,但 BYOL 直接引导潜在表征。
看似BYOL似乎实在进行自监督学习,而根本没有在不同图像之间形成对比。但是,看来BYOL起作用的主要原因是它正在通过一种间接机制进行某种形式的对比学习。通过对比上述三种方法的MLP结构,我们发现,BN的存在与否对网络性能影响很大,如果没有BN对于BYOL网络极容易出现模型坍塌(model collapse)。BN会显示的注入对负样本的依赖性,因为无论同一批次的输入多么相似,它们的值都会被重新分配(按照 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1)),因此BN有效地阻止了模型坍塌.
讨论
通过阅读这些经典文献工作,我自己的思考主要如下:
- 找到合适的辅助任务(pretext)对于自监督学习是最需要解决的问题。
- 数据和资源越多,自监督预训练的效果会更好(Bert, MoCo, SimCLR)。
- 自监督直接和具体任务的结合(Task Related Self-Supervised Learning)是个可探索的方向,已经在很多任务中初露头角,也比较符合审稿人的口味。
参考文献
[1] Alexey Dosovitskiy, et al. “Discriminative unsupervised feature learning with exemplar convolutional neural networks.” IEEE transactions on pattern analysis and machine intelligence 38.9 (2015): 1734-1747.
[2] Spyros Gidaris, Praveer Singh & Nikos Komodakis. “Unsupervised Representation Learning by Predicting Image Rotations” ICLR 2018.
[3] Carl Doersch, Abhinav Gupta, and Alexei A. Efros. “Unsupervised visual representation learning by context prediction.” ICCV. 2015.
[4] Mehdi Noroozi & Paolo Favaro. “Unsupervised learning of visual representations by solving jigsaw puzzles.” ECCV, 2016.
[5] Mehdi Noroozi, Hamed Pirsiavash, and Paolo Favaro. “Representation learning by learning to count.” ICCV. 2017.
[6] Richard Zhang, Phillip Isola & Alexei A. Efros. “Colorful image colorization.” ECCV, 2016.
[7] Pascal Vincent, et al. “Extracting and composing robust features with denoising autoencoders.” ICML, 2008.
[8] Jeff Donahue, Philipp Krähenbühl, and Trevor Darrell. “Adversarial feature learning.” ICLR 2017.
[9] Deepak Pathak, et al. “Context encoders: Feature learning by inpainting.” CVPR. 2016.
[10] Richard Zhang, Phillip Isola, and Alexei A. Efros. “Split-brain autoencoders: Unsupervised learning by cross-channel prediction.” CVPR. 2017.
[11] Xiaolong Wang & Abhinav Gupta. “Unsupervised Learning of Visual Representations using Videos.” ICCV. 2015.
[12] Carl Vondrick, et al. “Tracking Emerges by Colorizing Videos” ECCV. 2018.
[13] Ishan Misra, C. Lawrence Zitnick, and Martial Hebert. “Shuffle and learn: unsupervised learning using temporal order verification.” ECCV. 2016.
[14] Basura Fernando, et al. “Self-Supervised Video Representation Learning With Odd-One-Out Networks” CVPR. 2017.
[15] Donglai Wei, et al. “Learning and Using the Arrow of Time” CVPR. 2018.
[16] Florian Schroff, Dmitry Kalenichenko and James Philbin. “FaceNet: A Unified Embedding for Face Recognition and Clustering” CVPR. 2015.
[17] Pierre Sermanet, et al. “Time-Contrastive Networks: Self-Supervised Learning from Video” CVPR. 2018.
[18] Debidatta Dwibedi, et al. “Learning actionable representations from visual observations.” IROS. 2018.
[19] Eric Jang & Coline Devin, et al. “Grasp2Vec: Learning Object Representations from Self-Supervised Grasping” CoRL. 2018.
[20] Ashvin Nair, et al. “Visual reinforcement learning with imagined goals” NeuriPS. 2018.
[21] Ashvin Nair, et al. “Contextual imagined goals for self-supervised robotic learning” CoRL. 2019.
[22] Aaron van den Oord, Yazhe Li & Oriol Vinyals. “Representation Learning with Contrastive Predictive Coding” arXiv preprint arXiv:1807.03748, 2018.
[23] Olivier J. Henaff, et al. “Data-Efficient Image Recognition with Contrastive Predictive Coding” arXiv preprint arXiv:1905.09272, 2019.
[24] Kaiming He, et al. “Momentum Contrast for Unsupervised Visual Representation Learning.” CVPR 2020.
[25] Zhirong Wu, et al. “Unsupervised Feature Learning via Non-Parametric Instance-level Discrimination.” CVPR 2018.
[26] Ting Chen, et al. “A Simple Framework for Contrastive Learning of Visual Representations.” arXiv preprint arXiv:2002.05709, 2020.
[27] Aravind Srinivas, Michael Laskin & Pieter Abbeel “CURL: Contrastive Unsupervised Representations for Reinforcement Learning.” arXiv preprint arXiv:2004.04136, 2020.
[28] Carles Gelada, et al. “DeepMDP: Learning Continuous Latent Space Models for Representation Learning” ICML 2019.
[29] Amy Zhang, et al. “Learning Invariant Representations for Reinforcement Learning without Reconstruction” arXiv preprint arXiv:2006.10742, 2020.
[30] Xinlei Chen, et al. “Improved Baselines with Momentum Contrastive Learning” arXiv preprint arXiv:2003.04297, 2020.
[31] Jean-Bastien Grill, et al. “Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning” arXiv preprint arXiv:2006.07733, 2020.
[32] Abe Fetterman & Josh Albrecht. “Understanding self-supervised and contrastive learning with Bootstrap Your Own Latent (BYOL)” Untitled blog. Aug 24, 2020.
ps://arxiv.org/abs/2006.07733) arXiv preprint arXiv:2006.07733, 2020.
[32] Abe Fetterman & Josh Albrecht. “Understanding self-supervised and contrastive learning with Bootstrap Your Own Latent (BYOL)” Untitled blog. Aug 24, 2020.
[33]Self-Supervised Representation Learning
[34]Self-supervised Learning 再次入门
[35]Understanding self-supervised and contrastive learning with “Bootstrap Your Own Latent” (BYOL)
