Machine Learning with Graphs 之 Page Rank

一、 Overview

本节主要从矩阵的角度，来对graph进行分析与学习，当然之前所讲的eigenvector centrality以及katz index已经在算法中利用矩阵来进行节点或者边的features计算与设计，但除此之外，将graph视作一个矩阵，还能允许我们做更多的事，比如通过随机游走的方式来判断一个节点的重要性（PageRank），或者通过矩阵分解的方式来获得节点的embedding，当然随机游走，矩阵分解，节点特征从矩阵的角度来看彼此也是紧密联系着的。

二、 Page Rank

2.1 overview

PageRank, also known as Google Algorithm，是1998年，斯坦福大学博士生拉里·佩奇（lary page)和小伙伴谢尔盖·布林提出来的，主要是为了解决用户搜索结果的排序问题，并在此基础上研发了一款搜索引擎，即后来的巨无霸Google。
当然对于一个搜索引擎而言，往往需要有如下三步，而page rank主要关注的就是如何将一个重要并且可信的candidates排序在前面呈现在用户面前。当然这个步骤是可以与前面步骤并行的，即不依赖于前面的步骤，因此这也是Google检索速度快与准的一个原因。

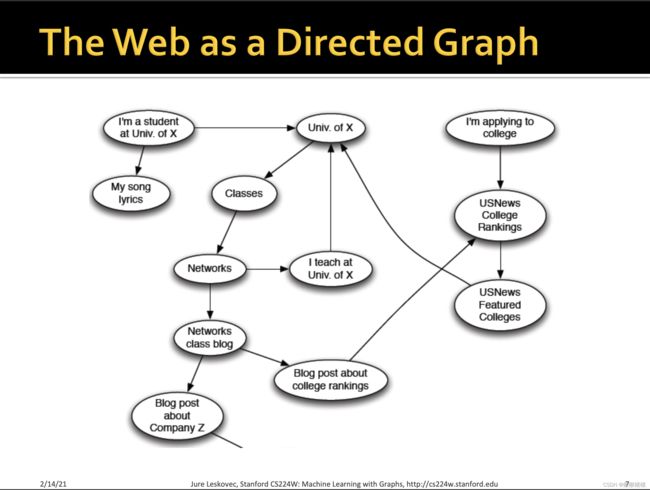
Web can be regarded as a big graph, namely the web pages are the nodes and the hyperlinks are the edges.

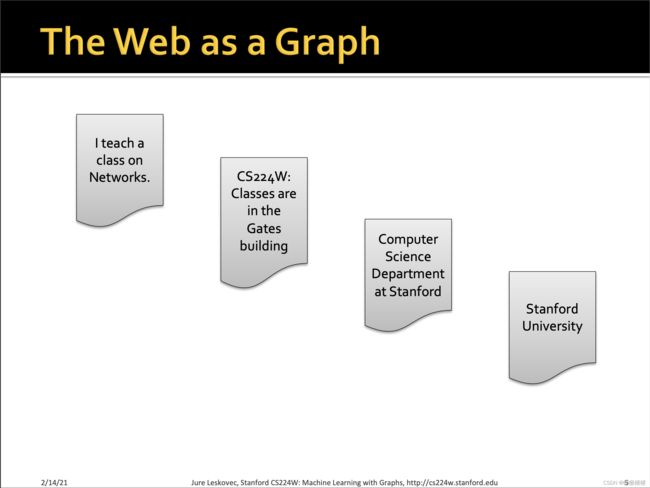
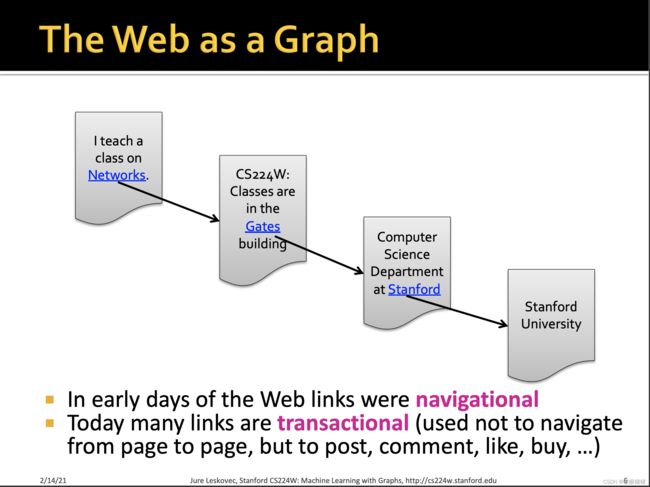如上所示，早期的互联网链接往往是navigational，即导航性质的，通过链接将分布在各处的网页彼此连接起来，如早期的门户网站，而今天的互联网连接，其性质更倾向于事务型，即往往用于发布，评论，点赞，购买等。比如知乎你的关注以及被关注，也可以组成一个graph。但无论是transanctional or navigational, 通常都将web视作一个有向图。
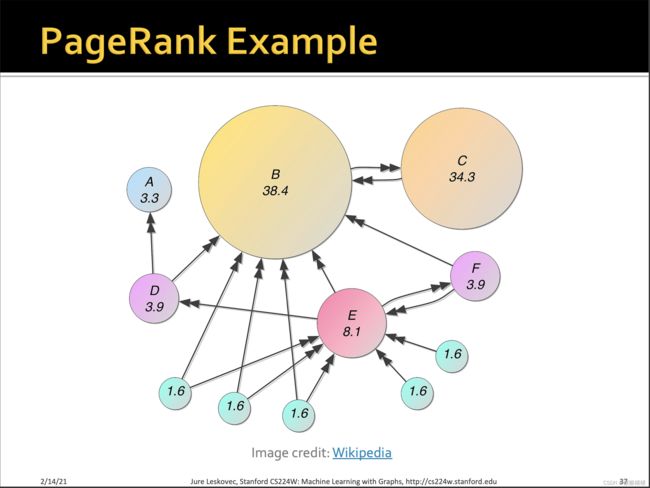
其他类似的信息网络，还包括论文引用，维基百科等，当初pagerank的提出也是受到了citations模式的启发。

既然我们已经知道了，web可以视作一个有向图，那么多对于浩如烟海的网页，我们怎样对web里面的page进行重要性排序呢？因为所有的pages并不是同等重要的。而后面我们所讨论的一系列算法，像本节的page rank, personalized pagerank, random walk with restart都是基于link analysis的方法。

其核心思想就是将links视作打分投票的依据，最naive的想法就是如果一个page拥有更多的边，它就拥有更高的得分，即重要性。当然，由于是一个有向图的关系，对于每一个节点而言，会涉及到in-coming links以及out-going links，这儿我们只将in-links作计票，因为out-links作弊空间太大了，不具备参考意义，对于一个node而言，它可以往外伸出无数条out-links，但是并不表明它很重要。
但又会遇到另外一个问题，即所有的links都拥有相同的分数吗？那显然也不是，往往将来自更重要的page的in-links置更大的得分，因为近朱者赤，你受到一个大v关注，或者你的论文被一个诺奖得主关注，那么你本身也就是大牛了。
因此计算page得分，本身是一个递归的问题，类似的思路是eigenvector centrality那一节已经讲过了，不做赘述，当然下面的很多思想也和eigenvector centrality一致，详情可见: https://blog.csdn.net/pku_langzi/article/details/121407331?spm=1001.2014.3001.5501

2.2 algorithm

一个page是重要的，当

1. 它拥有更多的邻居节点
2. 它的邻居很重要

在paper的原文是这样说的：

关于边的得分（vote）与节点的重要性（rank）有如下三条说明：

1. 每一个边（link）的得分正比于它source page的重要性
2. 如果page $i$的重要性是$r_i$，并且它有$d_i$条out-links，那么每一条link将获得$r_i/d_i$得分，即被稀释了
3. page $j$的重要性$r_j$是指向它的所有in-links的得分之和

我们称PageRank是一个flow model，而flow的正是这种rank得分
上述是对rank的定义以及边的vote的一个例子。
一个节点的rank得分$r$的计算方式如上。
当然，为了求解这样一个问题，我们可以用高斯消元法来求每个page的rank，即n个方程，n个未知数，
但有时候没有唯一解，因此也可以加一些限制，比如上面让 y + a + m = 1
可以解得到 y = 2/5 , a = 2 / 5, m = 1 / 5
但显然当n很大时，这并不是一个非常优雅且便捷的方式。

那么如果用矩阵的思路来formulate这个问题呢？

这儿初始化了一个随机邻接矩阵¹$M$，它的值$M_{ij}$表示的是从$j$向$i$传递的得分（power）（⚠️这儿的方向，易理解成 i 到 j），初始化为$M_{ij}=\frac{1}{d_j}$，是一个列随机矩阵，故$M$的每个列向量之和是为1的。
在计算每个page的得分时，由于是一个递归的计算方式，因此与之前的eigen vector或者power vector类似，可以写成矩阵与向量的乘积形式，引入了一个rank vector $r$的概念，
$$\begin{gathered} r=M.r \\ {r}_j=\sum _{i\mapsto j}\frac{r_i}{d_i} \end{gathered}$$
其中rank vector中的每一个元素（entry）$r_i$表示的就是page $i$的重要性，并且进行了归一化，让$\sum _i{r}_i=1$。

因此整个flow的过程，可以表征为上面矩阵与向量相乘的形式。

原文的一些说明：

这儿举了一个例子，对于这么一个简单的network，包含三个page，分别是 $y,a,m$，初始化flow矩阵$M$为右上角所示的matrix。其中$M_{ij}$表示的是$j\mapsto i$的边的得分，因为每个page的初始化重要性为1，因此对于每一个列而言，重要性1被出度$d_j$所平分，分别传递给page $i$。比如$M_{00}$表示的是从$y\mapsto y$的vote，为$\frac{1}{2}$，因为y总共有两条outlinks，其中$y\mapsto y$分得$\frac{1}{2}$，而$y\mapsto a$分得$\frac{1}{2}$。对于这个随机矩阵或者叫转移矩阵而言，graph如果一旦固定，其就不会变的。
然后我们就可以分别计算三个page的rank
$$\begin{gathered} r_y=r_y/2+r_a/2 \\ {r}_a=r_y/2+r_m \\ {r}_m=r_a/2 \end{gathered}$$
表示为矩阵向量的形式的话，就如右所示。

这儿可以与随机游走进行联系，想象这是一个随机的游走者（冲浪人），当$t$时刻他位于page $i$，那么在$t+1$时刻，他将通过$i$的out-links按均匀分布地随机走到下一个网页$j$，并且无限地随机游走下去。如果让一个向量$p(t)$，它的$i^{th}$个位置的值表示在$t$时刻访问page $i$的概率，所以整个$p(t)$可以用来表示网页的一个概率分布。
那么$t+1$时刻达到各个网页的概率分布$p(t+1)=M.p(t)$，假设随机游走到达一个新的状态的分布满足
$$p(t+1)=M.p(t)=p(t)$$
那么$p(t)$是一个随机游走固定不变的分布（这儿有点困惑，感觉是个先有蛋还是先有鸡的问题），后面会证明其收敛性。
先前所讲的rank vector满足$r=M.r$，因此r是一个固定不变的随机游走分布。

这个悠闲上网者看到转移矩阵M，他在想，这个M矩阵就代表了当前整个网络的拓朴结构，那么这个拓朴结构背后一定隐含了某种规律，这个规律就是每个网页的权重。这个规则“支撑”着网络成为今天我看到的样本。那我要努力去游走，让我的评价无限接近网络背后的真实规律。恩，加油，我一定行的！

其实$p(t+1)=M.p(t)$就是一个马尔可夫过程²

联系之前的eigenvector定义，可以发现这个rank vector与eigenvector是极其相似的，当时我们用power iteration来迭代收敛到eigenvector，并证明其收敛性以及矩阵$A$最大的特征值对应的特征向量都我们所需的eigenvector（其每个entry都>0），只不过值得注意的地方在于，eigenvector是针对无向图的，而rank vectors是针对有向图的。

如果用eigenvector的思路来阐述的话，
$$1.r=M.r$$
此时的rank vector $r$就是随机邻接矩阵$M$在特征值为1的时候的特征向量。然后通过poser iteration的方式来求$r$。
具体怎么求，可以参考我之前的博客对eigenvector推导的补充Machine Learning with Graphs 之 Traditional Methods for Machine Learning in Graphs，或者继续下面章节的学习。

上面这页ppt将random walk与eigenvector进行了联系与统一，但其实上面ppt有几点是略讲了的：

1. 随机矩阵M一定存在特征值1吗？
2. 特征值1对应的特征向量唯一吗？

对于第一点而言，回答是yes:

对于第二点而言，回答是no (后面的page rank算法，对下面所提的孤岛问题或者叫trap问题会做解决）

2.3 how to solve

通过迭代的方式，先初始化值，然后迭代，直到$t+1$时刻与$t$时刻的经验误差小于$ϵ$。

More specifically, 经过不停的迭代迭代，直到
$$|r-r^{\prime }|<ϵ$$

那么灵魂三问：

• 它一定会收敛吗？
• 它收敛的值是我们想要的吗？
• 结果合理吗？
  我们首先看naive的pagerank遇到的两个问题，就可以回答上面的灵魂三问：
• dead ends
• spider traps

其中spider trap指的是

其中dead end指的是：

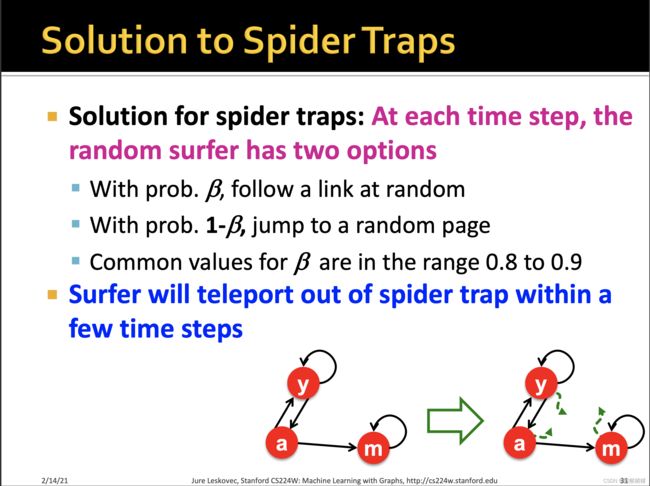
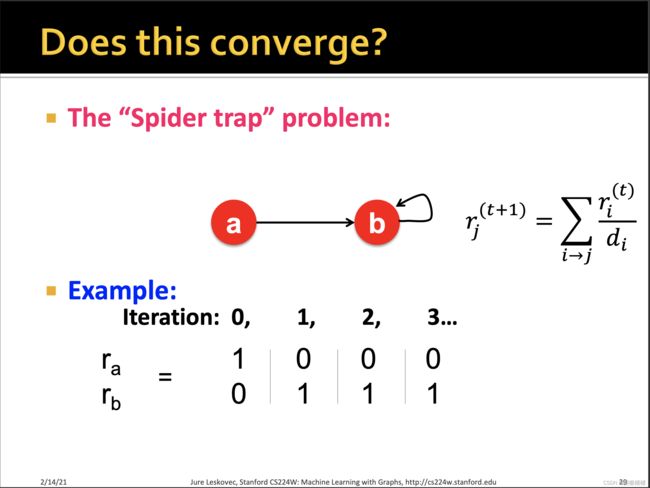
见招拆招，为了跳出spider trap，那么在每一个时刻，这个随机游走的surfer下一步有两种选择

1. 以$\beta$的概率顺着link随机往下走
2. 以 $1-\beta$ 的概率，跳到一个随机的网页

其中$\beta$往往取值在0.8 - 0.9之间，这个$\beta$也被称为阻尼系数，因此在一定数目的step之后，surfer将跳出spider trap。

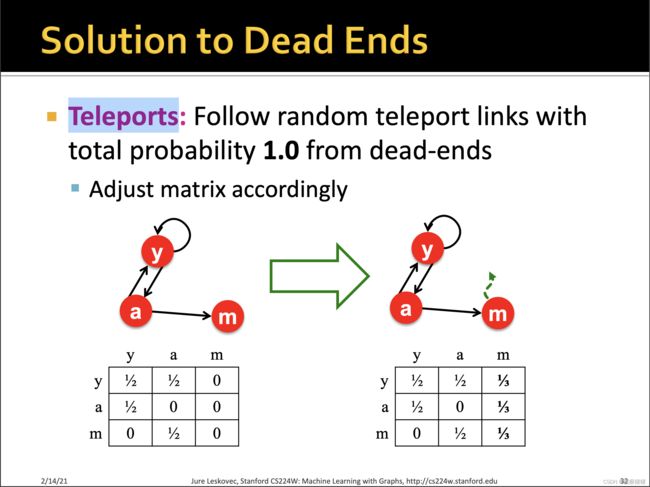其实spider trap不是致命的，因为至少它满足了随机矩阵的定义，而dead ends是某一列为0，那么必然会收敛到0.
为了避免dead ends，想到的方式是传送，对于dead-ends的page，让其有随机的概率跳转到任意的网页，概率之和为1。

那么此时这个Google Matrix其特征值1对应的特征向量唯一吗？

与上面证明所举的反例相比，前者是一个disconnected graph，而目前的G是一个强连接图strongly connected graph（并且是一个里面的值都>0的graph），因此目前可以回答是yes了，证明如下：

证明的思路是这样的，假设M的特征值1存在线性无关的特征向量v, w，那么对于任意的实数s和t，sv + tw也是在1的特征向量空间里面，首先证明了1对应的特征向量里面的值都是>0或者都是<0的，那么sv + tw就会导致该向量里面同时存在正数和负数，那么必然v,2是线性相关的，反正得到1对应的特征向量空间的唯一性
因此关键点就变成了证明1对应的特征向量里面的值都是>0或者都是<0的。证明如下：

不可能存在一个为0，其他为正的情况，要么全为0，要么全为或者全为负，因为特征向量不能为0向量，所以特征向量值要么全为正，要么全为负，即空间唯一性质。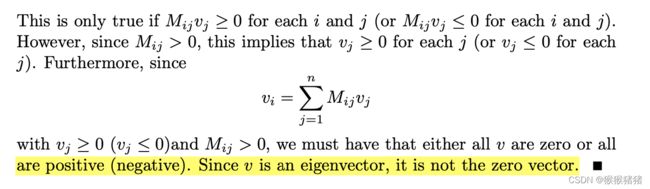那么此时我们来回答前面的灵魂三问呢？

1. 极限是否存在？

2. 如果极限存在，它是否与初始值$p_0$的选取有关？即收敛性是否初始值敏感？

3. 如果极限存在，并且与的选取初始值$p_0$无关，它作为网页排序的依据是否真的合理？

因为随机过程理论中有一个所谓的马尔可夫链基本定理 (fundamental theorem of Markov chains)， 它表明在一个马尔可夫过程中， 如果转移矩阵是素矩阵， 那么上述前两个问题的答案就是肯定的。 而随机性修正已经解决了上述第三个问题， 因此所有问题就都解决了。

原文轻描淡写一句：we built a web search engine called Google. 殊不知将成为未来最伟大的科技公司。

三、 Reference

参考：PageRank算法初探

参考：谷歌背后的数学

参考： Math 443/543 Graph Theory Notes 6: Graphs as matrices and PageRank

参考：https://courses.helsinki.fi/sites/default/files/course-material/4545800/stochastic.pdf

参考：http://snap.stanford.edu/class/cs246-2012/slides/09-pagerank.pdf

---

1. 随机矩阵
   随机矩阵又叫做概率矩阵（probability matrix）、转移矩阵（transition matrix）、马尔科夫矩阵（markov matrix）等。
   随机矩阵实际是非负矩阵(Nonnegative matrix)的一类，而非负矩阵是指矩阵元素都是非负(Nonnegative)的。
   随机矩阵通常表示左随机矩阵（left stochastic matrix），即“列和”为1
   对任意的随机矩阵，其谱半径是1，即最大特征值是1，其对应的特征向量里面的每个元素都>0 或都< 0。
   随机矩阵的主特征值以及second largest eigenvalue的比值是幂法收敛速度的一个基本的衡量标准。 ↩︎

2. 马尔可夫随机过程
   马尔可夫过程， 也称为马尔可夫链 (Markov chain)， 是一类离散随机过程， 它的最大特点是每一步的转移概率分布都只与前一步有关。 而平稳马尔可夫过程则是指转移概率分布与步数无关的马尔可夫过程 (体现在我们的例子中， 即 H 与 n 无关)。 另外要说明的是， 本文在表述上不同于佩奇和布林的原始论文， 后者并未使用诸如 “马尔可夫过程” 或 “马尔可夫链” 那样的术语， 也并未直接运用这一领域内的数学定理。 ↩︎