MATLAB实现智能计算方法实验:实验五 Hopfield神经网络
资源链接
MATLAB实现智能计算方法课程所有实验代码资源链接为:MATLAB实现智能计算方法课程所有实验代码资源
实验汇总
MATLAB实现智能计算方法课程所有实验汇总博客链接为:MATLAB实现智能计算方法实验汇总
实验目的
- 通过本次实验,进一步理解Hopfield网络的模型结构与计算原理;
- 掌握手工计算过程和编码,并能够解决实际问题;
- 掌握MATLAB工具箱中的Hopfield相关函数,用工具箱实现编程,解决实际问题。
实验内容
在三维平面上,定义两个平衡点(1,-1,1)和(-1,1,-1),使所有的输入向量经过迭代最后都收敛到这两个点。
- 给出手工计算过程,并用代码(python或matlab)实现;
- 设计网络结构(以图的形式放入报告);
- 用MATLAB工具箱编程实现模型仿真。
实验步骤
1. 手工计算及编码
根据权值计算公式: w i j = { 1 n ∑ k = 1 m u i k u j k , j ≠ i 0 , j = i {w_{ij}} = \left\{ \begin{array}{l} \frac{1}{n}\sum\limits_{k = 1}^m {u_i^ku_j^k,j \ne i} \\ 0,j = i \end{array} \right. wij=⎩⎨⎧n1k=1∑muikujk,j=i0,j=i
用矩阵形式表示: w = 1 n ( ∑ k = 1 m U k U k T − m I ) w=\frac{1}{n}(\sum\limits_{k=1}^{m}{U_{k}^{{}}U_{k}^{T}-mI)} w=n1(k=1∑mUkUkT−mI)
求得权值矩阵为:
1 3 × ( [ 1 − 1 − 1 1 1 − 1 ] × [ 1 − 1 1 − 1 1 − 1 ] − 2 × [ 1 0 0 0 1 0 0 0 1 ] ) = 1 3 × [ 0 − 2 2 − 2 0 − 2 2 − 2 0 ] \frac{{\rm{1}}}{{\rm{3}}} \times \left( {\left[ \begin{array}{l} 1 & -1\\ -1 & 1\\ 1 & -1 \end{array} \right] \times \left[ \begin{array}{l} 1 & -1 & 1\\ -1 & 1 & -1 \end{array} \right] - 2 \times \left[ \begin{array}{l} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right]} \right) = \frac{{\rm{1}}}{{\rm{3}}} \times \left[ \begin{array}{l} 0 & - 2 & 2\\ -2 & 0 & -2\\ 2 & - 2 & 0 \end{array} \right] 31×⎝⎛⎣⎡1−11−11−1⎦⎤×[1−1−111−1]−2×⎣⎡100010001⎦⎤⎠⎞=31×⎣⎡0−22−20−22−20⎦⎤
假设某一次输入的向量为: [ 0.8 − 0 . 7 0 . 9 ] \left[ \begin{array}{l} 0.8\\ {\rm{ - 0}}{\rm{.7}}\\ {\rm{0}}{\rm{.9 }} \end{array} \right] ⎣⎡0.8−0.70.9⎦⎤选择更新第二个神经元,根据公式 v i ( t + 1 ) = S g n [ ∑ j = 1 N w i j x j ( n ) ] {v_i}(t + 1) = Sgn[\sum\limits_{j = 1}^N {w_{ij}^{}x_j^{}(n)]} vi(t+1)=Sgn[j=1∑Nwijxj(n)]一次计算过程如下:
w i j x j ( n ) = 1 3 × [ − 2 0 − 2 ] × [ 0.8 − 0 . 7 0 . 9 ] = − 1 . 13 w_{ij}^{}x_j^{}(n) = \frac{{\rm{1}}}{{\rm{3}}} \times \left[\begin{array}{l} -2 & 0 & -2 \end{array}\right] \times \left[ \begin{array}{l} 0.8\\ {\rm{ - 0}}{\rm{.7}}\\ {\rm{0}}{\rm{.9 }} \end{array} \right] = - {\rm{1}}{\rm{.13}} wijxj(n)=31×[−20−2]×⎣⎡0.8−0.70.9⎦⎤=−1.13
整个仿真过程通过编程实现,根据题意及上述计算过程,设计有两个记忆模式,每个记忆模式有三个分量的Hopfield神经网络,激励函数选择符号函数,代码如下:
clc;
clear;
T = [1 -1 1; -1 1 -1]';
[n, m] = size(T);
%计算网络权值
w = zeros(n, n);
for i = 1: m
w = w + T(:, i)*T(:, i)';
end
w = (1/3)*(w - m*eye(n, n));
axis([-1 1 -1 1 -1 1]);
set(gca, 'box', 'on');
axis manual;
plot3(T(1, :), T(2, :), T(3, :), 'rp');%rp表示红色五角星
title('含有三个神经元的Hopfield网络状态空间');
xlabel('a(1)'); ylabel('a(2)'); zlabel('a(3)'); view([-36 30]); hold on;
%随机选取50个数进行仿真
for m = 1: 50
v1 = rands(3);
v0 = v1;
n = length(v0);
v = zeros(n, 1);
while(sum(v ~= v0)~=0 || sum(abs(v0) - ones(n, 1)) ~= 0)
v = v0;
i = randi(n);
if(w(i, :)*v0<0)
v0(i, :) = -1;
else
v0(i, :) = 1;
end
end
track = [v1 v0];
plot3(v1(1, 1), v1(2, 1), v1(3, 1), 'k+', track(1, :), track(2, :), track(3, :));
hold on;
end
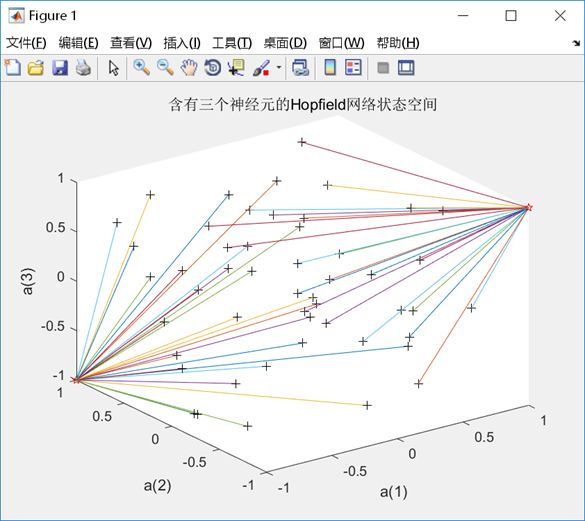
运行程序,结果如下图1。
由图可知,随机产生的输入向量经过迭代最后都收敛到设定的两个点。
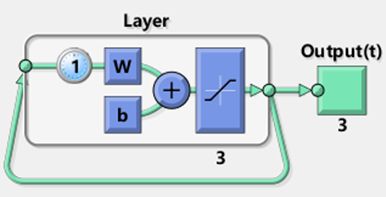
2. 设计网络结构
设计Hopfield网络结构如下图。
3. 工具箱仿真
用MATLAB工具箱编程实现模型仿真,程序代码如下:
clc;
clear;
T=[1 -1 1; -1 1 -1]';
axis([-1 1 -1 1 -1 1]);
set(gca,'box', 'on');
axis manual;
hold on;
plot3(T(1, :), T(2, :),T(3, :), 'rp');
title('含有三个神经元的Hopfield网络状态空间');
xlabel('a(1)');
ylabel('a(2)');
zlabel('a(3)');
view([-36 30]);
%设计网络
net = newhop(T);
%随机选取50个初始点进行赋值,观察结果。
color = 'rgbmy';
for i = 1: 50
a={rands(3, 1)};
[y, Pf, Af] = sim(net, {1, 10}, {}, a);
record = [cell2mat(a) cell2mat(y)];
start = cell2mat(a);
plot3(start(1, 1), start(2, 1), start(3, 1), 'k+', record(1, :), record(2, :), record(3, :), color(rem(i, 5) + 1));
end
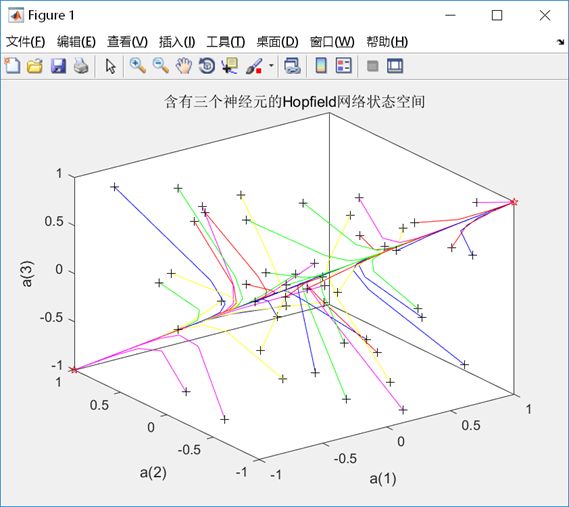
执行程序,运行结果如下图3。