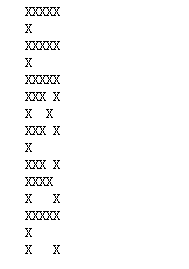人工智能 实验5.Hopfield神经网络
实验五 Hopfield神经网络
Keras中文文档:https://keras.io/zh/models/sequential/
一、实验目的与要求
1)掌握离散型Hopfield神经网络的原理和网络结构。
2)了解Hopfield神经网络的应用和优化方法。
二、实验内容
1)离散Hopfield神经网络的实现,给记忆样本加30%的噪声,再根据hopfield的特性循环n次,实现记忆样本的还原。
记忆样本,4个5x5的矩阵(来源于网络,分别表示字母N,E,R,0):
sample = [[1,-1,-1,-1,1,
1,1,-1,-1,1,
1,-1,1,-1,1,
1,-1,-1,1,1,
1,-1,-1,-1,1],
[1,1,1,1,1,
1,-1,-1,-1,-1,
1,1,1,1,1,
1,-1,-1,-1,-1,
1,1,1,1,1],
[1,1,1,1,-1,
1,-1,-1,-1,1,
1,1,1,1,-1,
1,-1,-1,1,-1,
1,-1,-1,-1,1],
[-1,1,1,1,-1,
1,-1,-1,-1,1,
1,-1,-1,-1,1,
1,-1,-1,-1,1,
-1,1,1,1,-1]]
实现的最后结果应该是: 从上到下,第一张为记忆样本、第二张为加噪的记忆样本、第三张为循环n(可设具体数值,比如2000等)次后回忆出的结果。
代码实例:
| #1.根据Hebb学习规则计算神经元之间的连接权值 def calcWeight(savedsample): N = len(savedsample[0]) P = len(savedsample) mat = [0]*N returnMat = [] for i in range(N): m = mat[:] returnMat.append(m) for i in range(N): for j in range(N): if i==j: continue sum = 0 for u in range(P): sum += savedsample[u][i] * savedsample[u][j] returnMat[i][j] = sum/float(N) return returnMat
#2. 根据神经元的输入计算神经元的输出(静态突触) def calcXi(inMat , weighMat): returnMat = inMat choose = [] for i in range(len(inMat)/5): #随机改变N/5个神经元的值,该参数可调,也可同时改变所有神经元的值 choose.append(random.randint(0,len(inMat)-1)) for i in choose: sum = 0 for j in range(len(inMat)): sum += weighMat[i][j] * inMat[j] if sum>=0: returnMat[i] = 1 else: returnMat[i] = -1 return returnMat #记忆样本 sample = [[1,-1,-1,-1,1, 1,1,-1,-1,1, 1,-1,1,-1,1, 1,-1,-1,1,1, 1,-1,-1,-1,1], [1,1,1,1,1, 1,-1,-1,-1,-1, 1,1,1,1,1, 1,-1,-1,-1,-1, 1,1,1,1,1], [1,1,1,1,-1, 1,-1,-1,-1,1, 1,1,1,1,-1, 1,-1,-1,1,-1, 1,-1,-1,-1,1], [-1,1,1,1,-1, 1,-1,-1,-1,1, 1,-1,-1,-1,1, 1,-1,-1,-1,1, -1,1,1,1,-1]] #加噪函数,在记忆样本的基础上增加30%的噪声 def addnoise(mytest_data,n): for x in range(n): for y in range(n): if random.randint(0, 10) > 7: mytest_data[x * n + y] = -mytest_data[x * n + y] return mytest_data #对样本测试,进行记忆样本的迭代和还原: #请输入代码 |
2)(选做题)回忆起原始图片。通过Hopfield神经网络存储一张二值图片,根据某个阈值色度可将每一张图片导出为0-1图片。利用输入的训练图片,获得权重矩阵,或者耦合系数矩阵之后,将该记忆矩阵保存。对图片进行加噪,依然将图片矩阵化,得到二值矩阵。进行迭代,最后,测试图片迭代至稳态或者亚稳态,此时的状态即可认为网络已回忆起原始图片。
图像实例:
测试图像:
代码实现
| #导入库,包 import numpy as np import random from PIL import Image import os import re import matplotlib.pyplot as plt from IPython.core.interactiveshell import InteractiveShell InteractiveShell.ast_node_interactivity = "all"
#将jpg格式或者jpeg格式的图片转换为二值矩阵。先生成x这个全零矩阵,从而将imgArray中的色度值分类,获得最终的二值矩阵。 def readImg2array(file,size, threshold= 145): #file is jpg or jpeg pictures #size is a 1*2 vector,eg (40,40) pilIN = Image.open(file).convert(mode="L") pilIN= pilIN.resize(size) #pilIN.thumbnail(size,Image.ANTIALIAS) imgArray = np.asarray(pilIN,dtype=np.uint8) x = np.zeros(imgArray.shape,dtype=np.float) x[imgArray > threshold] = 1 x[x==0] = -1 return x
#逆变换 def array2img(data, outFile = None):
#data is 1 or -1 matrix y = np.zeros(data.shape,dtype=np.uint8) y[data==1] = 255 y[data==-1] = 0 img = Image.fromarray(y,mode="L") if outFile is not None: img.save(outFile) return img
#利用x.shape得到矩阵x的每一维个数,从而得到m个元素的全零向量。将x按i\j顺序赋值给向量tmp1. 最后得到从矩阵转换的向量。 def mat2vec(x): #x is a matrix m = x.shape[0]*x.shape[1] tmp1 = np.zeros(m)
c = 0 for i in range(x.shape[0]): for j in range(x.shape[1]): tmp1[c] = x[i,j] c +=1 return tmp1
#创建权重矩阵根据权重矩阵的对称特性,可以很好地减少计算量。 #请填写代码
#输入test picture之后对神经元的随机升级。利用异步更新,获取更新后的神经元向量以及系统能量。 #randomly update def update_asynch(weight,vector,theta=0.5,times=100): energy_ = [] times_ = [] energy_.append(energy(weight,vector)) times_.append(0) for i in range(times): length = len(vector) update_num = random.randint(0,length-1) next_time_value = np.dot(weight[update_num][:],vector) - theta if next_time_value>=0: vector[update_num] = 1 if next_time_value<0: vector[update_num] = -1 times_.append(i) energy_.append(energy(weight,vector))
return (vector,times_,energy_) #为了更好地看到迭代对系统的影响,我们按照定义计算每一次迭代后的系统能量,最后画出E的图像,便可验证。
def energy(weight,x,bias=0): #weight: m*m weight matrix #x: 1*m data vector #bias: outer field energy = -x.dot(weight).dot(x.T)+sum(bias*x) # E is a scalar return energy #调用前文定义的函数把主函数表达清楚。可以调整size和threshod获得更好的输入效果为了增加泛化能力,正则化之后打开训练图片,并且通过该程序获取权重矩阵。 #请输入代码 #测试图片 #请输入代码 利用对测试图片的矩阵(神经元状态矩阵)进行更新迭代,直到满足我们定义的迭代次数。最后将迭代末尾的矩阵转换为二值图片输出。 #plt.show() oshape = matrix_test.shape aa = update_asynch(weight=w_,vector=vector_test,theta = 0.5 ,times=8000) vector_test_update = aa[0] matrix_test_update = vector_test_update.reshape(oshape) #matrix_test_update.shape #print(matrix_test_update) plt.subplot(222) plt.imshow(array2img(matrix_test_update)) plt.title("recall"+str(num))
#plt.show() plt.subplot(212) plt.plot(aa[1],aa[2]) plt.ylabel("energy") plt.xlabel("update times")
plt.show()
|
代码实验1
# -*- coding: utf-8 -*-
import random
#1.根据Hebb学习规则计算神经元之间的连接权值
#Hebb学习规则是一个无监督学习规则,这种学习的结果是使网络能够提取训练集的统计特性,从而把输入信息按照它们的相似性程度划分为若干类。
#即根据事物的统计特征进行分类。Hebb学习规则只根据神经元连接间的激活水平改变权值,因此这种方法又称为相关学习或并联学习。
#Hebb的理论认为在同一时间被激发的神经元间的联系会被强化
def calcWeight(savedsample):
N = len(savedsample[0])#一个字母的存储长度
P = len(savedsample)#存储的字母个数
mat = [0]*N#mat矩阵与一个字母矩阵大小同,全置为0
returnMat = []#返回矩阵为n*mat
for i in range(N):
m = mat[:]
returnMat.append(m)
for i in range(N):
for j in range(N):
if i==j:
continue#相同位置为0
sum = 0
for u in range(P):#遍历各个矩阵中对应的这两位置
sum += savedsample[u][i] * savedsample[u][j]
returnMat[i][j] = sum/float(N)#i->j的权值为各[i]*[j]/N
return returnMat
#2. 根据神经元的输入计算神经元的输出(静态突触)
def calcXi(inMat , weighMat):
returnMat = inMat
choose = []
#随机回忆N/5个神经元的值,该参数可调,也可同时改变所有神经元的值
for i in range(int(len(inMat)/5)):
choose.append(random.randint(0,len(inMat)-1))
for i in choose:
sum = 0
for j in range(len(inMat)):#遍历i到所有输入像素
sum += weighMat[i][j] * inMat[j]
if sum>=0:
returnMat[i] = 1
else: returnMat[i] = -1
return returnMat
#加噪函数,在记忆样本的基础上增加30%的噪声
def addnoise(mytest_data,n):
for x in range(n):#行
for y in range(n):#列
if random.randint(0, 10) > 7:#30%
mytest_data[x * n + y] = -mytest_data[x * n + y]
return mytest_data
#显示输出
def regularout(data,N):
for j in range(N):
ch = ""
for i in range(N):
ch += " " if data[j*N+i] == -1 else "X"
print(ch)
#记忆样本
sample = [[1,-1,-1,-1,1,
1,1,-1,-1,1,
1,-1,1,-1,1,
1,-1,-1,1,1,
1,-1,-1,-1,1],
[1,1,1,1,1,
1,-1,-1,-1,-1,
1,1,1,1,1,
1,-1,-1,-1,-1,
1,1,1,1,1],
[1,1,1,1,-1,
1,-1,-1,-1,1,
1,1,1,1,-1,
1,-1,-1,1,-1,
1,-1,-1,-1,1],
[-1,1,1,1,-1,
1,-1,-1,-1,1,
1,-1,-1,-1,1,
1,-1,-1,-1,1,
-1,1,1,1,-1]]
weightMat = calcWeight(sample)
#for i in range(4):
# regularout(sample[i],5)
regularout(sample[1],5)
test = addnoise(sample[1],5)
regularout(test,5)
for i in range(2000):
test = calcXi(test,weightMat)
regularout(test,5)
实验二代码
如果报错PIL not named
需要conda install Pillow
# -*- coding: utf-8 -*-
"""
Created on Thu Apr 4 08:28:58 2019
@author: admin
"""
import numpy as np
import random
from PIL import Image
import os
import re
import matplotlib.pyplot as plt
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
#将jpg格式或者jpeg格式的图片转换为二值矩阵。先生成x这个全零矩阵,从而将imgArray中的色度值分类,获得最终的二值矩阵。
def readImg2array(file,size, threshold= 145):
#file is jpg or jpeg pictures
#size is a 1*2 vector,eg (40,40)
pilIN = Image.open(file).convert(mode="L")
pilIN= pilIN.resize(size)
#pilIN.thumbnail(size,Image.ANTIALIAS)
imgArray = np.asarray(pilIN,dtype=np.uint8)
x = np.zeros(imgArray.shape,dtype=np.float)
x[imgArray > threshold] = 1
x[x==0] = -1
return x
def create_W_single_pattern(x):
# x is a vector
if len(x.shape) != 1:
print ("The input is not vector")
return
else:
w = np.zeros([len(x),len(x)])
for i in range(len(x)):
for j in range(i,len(x)):
if i == j:
w[i,j] = 0
else:
w[i,j] = x[i]*x[j]
w[j,i] = w[i,j]
return w
#逆变换
def array2img(data, outFile = None):
#data is 1 or -1 matrix
y = np.zeros(data.shape,dtype=np.uint8)
y[data==1] = 255
y[data==-1] = 0
img = Image.fromarray(y,mode="L")
if outFile is not None:
img.save(outFile)
return img
#利用x.shape得到矩阵x的每一维个数,从而得到m个元素的全零向量。将x按i\j顺序赋值给向量tmp1. 最后得到从矩阵转换的向量。
def mat2vec(x):
#x is a matrix
m = x.shape[0]*x.shape[1]
tmp1 = np.zeros(m)
c = 0
for i in range(x.shape[0]):
for j in range(x.shape[1]):
tmp1[c] = x[i,j]
c +=1
return tmp1
#创建权重矩阵根据权重矩阵的对称特性,可以很好地减少计算量。
#请填写代码
#输入test picture之后对神经元的随机升级。利用异步更新,获取更新后的神经元向量以及系统能量。
#randomly update
def update_asynch(weight,vector,theta=0.5,times=100):
energy_ = []
times_ = []
energy_.append(energy(weight,vector))
times_.append(0)
for i in range(times):
length = len(vector)
update_num = random.randint(0,length-1)
next_time_value = np.dot(weight[update_num][:],vector) - theta
if next_time_value>=0:
vector[update_num] = 1
if next_time_value<0:
vector[update_num] = -1
times_.append(i)
energy_.append(energy(weight,vector))
return (vector,times_,energy_)
#为了更好地看到迭代对系统的影响,我们按照定义计算每一次迭代后的系统能量,最后画出E的图像,便可验证。
def energy(weight,x,bias=0):
#weight: m*m weight matrix
#x: 1*m data vector
#bias: outer field
energy = -x.dot(weight).dot(x.T)+sum(bias*x)
# E is a scalar
return energy
#调用前文定义的函数把主函数表达清楚。可以调整size和threshod获得更好的输入效果为了增加泛化能力,正则化之后打开训练图片,并且通过该程序获取权重矩阵。
#请输入代码
#测试图片
#请输入代码
#利用对测试图片的矩阵(神经元状态矩阵)进行更新迭代,直到满足我们定义的迭代次数。最后将迭代末尾的矩阵转换为二值图片输出。
#plt.show()
size_global =(80,80)
threshold_global = 60
train_paths = []
#train_path = "/Users/admin/Desktop/train_pics/"
train_path = "train_pics/"
for i in os.listdir(train_path):
if re.match(r'[0-9 a-z A-Z-_]*.jp[e]*g',i):
train_paths.append(train_path+i)
flag = 0
for path in train_paths:
matrix_train = readImg2array(path,size = size_global,threshold=threshold_global)
vector_train = mat2vec(matrix_train)
plt.imshow(array2img(matrix_train))
plt.title("train picture"+str(flag+1))
plt.show()
if flag == 0:
w_ = create_W_single_pattern(vector_train)
flag = flag +1
else:
w_ = w_ +create_W_single_pattern(vector_train)
flag = flag +1
w_ = w_/flag
print("weight matrix is prepared!!!!!")
test_paths = []
#test_path = "/Users/admin/Desktop/test_pics/"
test_path = "test_pics/"
for i in os.listdir(test_path):
if re.match(r'[0-9 a-z A-Z-_]*.jp[e]*g',i):
test_paths.append(test_path+i)
num = 0
for path in test_paths:
num = num+1
matrix_test = readImg2array(path,size = size_global,threshold=threshold_global)
vector_test = mat2vec(matrix_test)
plt.subplot(221)
plt.imshow(array2img(matrix_test))
plt.title("test picture"+str(num))
oshape = matrix_test.shape
aa = update_asynch(weight=w_,vector=vector_test,theta = 0.5 ,times=8000)
vector_test_update = aa[0]
matrix_test_update = vector_test_update.reshape(oshape)
#matrix_test_update.shape
#print(matrix_test_update)
plt.subplot(222)
plt.imshow(array2img(matrix_test_update))
plt.title("recall"+str(num))
#plt.show()
plt.subplot(212)
plt.plot(aa[1],aa[2])
plt.ylabel("energy")
plt.xlabel("update times")
plt.show()