图像处理(第八章,图像分割、阈值、边缘、区域、二值图像处理、膨胀、腐蚀、开运算、闭运算、数学形态学)
图像处理第八章
- 第八章图像分割
-
- 8.1图像分割定义
- 8.2使用阈值进行图像分割
-
- 8.2.1固定阈值
- 8.2.2自动阈值
- 8.2.3最佳阈值
-
- 8.2.3.1直方图技术
-
- 直方图生成代码imhist()
- 8.2.3.2最大类间方差法(OTSU)
- 8.2.3.3 迭代法求阈值
- 8.2.4分水岭分割算法
- 8.3边缘检测和连接
-
- 8.3.1边缘检测
- 8.3.2边缘连接
- 8.4区域分割(区域算法利用像素的相似性)
-
- 8.4.1区域生长法(了解即可)
- 8.4.1区域分裂合并法(ppt里没有)
- 8.5二值图像处理
-
- 8.5.1数学形态学图像处理
-
- 8.5.1.1概述与集合论基础知识(重点)
- 8.5.1.2膨胀
- 8.5.1.3腐蚀
- 8.5.1.4应用
- 8.5.2开运算与闭运算
-
- 8.5.2.1开运算
- 8.5.2.2闭运算
- 8.5.3数学形态学应用算法
-
- 8.5.3.1边界提取
- 8.5.3.2区域填充
- 8.5.3.3连通分量的提取
第八章图像分割
8.1图像分割定义
(1)图像分割处理定义
将数字图像划分成互不相交(不重叠)区域的过程
(2)区域定义
像素的连通集
(3)连通定义
在一个连通集中的任意两个像素之间,存住一条完全由这个集合的元素构成的连通路径。
8.2使用阈值进行图像分割
8.2.1固定阈值
(1)定义
将整个图像中的灰度阈值的值设置为常数。
前提条件:如果背景的灰度值在整个图像中可合理地看作为恒定,而且所有物体与背景都具有几乎相同的对比度,那么,只要选择了正确的阈值,使用一个固定的阈值一般会有较好的效果。
8.2.2自动阈值
固定阈值的改进方法:使用自动阈值。
在许多的情况下,背景的灰度值并不是常数,物件和背景的对比度在图像中也有变化,这时,一个在图像中某一区域效果良好的阈值在其它区域却可能效果很差。在这种情况下,把灰度阈值取成一个随图像中位置缓慢变化的函数值是适宜的。
在有些著作中,自适应阈值被称为动态阈值。
8.2.3最佳阈值
除非图像中的物体有陡峭的边沿,否则灰度阈值的取值对所抽取物体的边界的定位和整体的尺寸有很大的影响。这意味着后续的尺寸(特别是面积)的测量对于灰度阈值的选择很敏感。由于这个原因,我们需要一个最佳的,或至少是具有一致性的方法确定阈值。
8.2.3.1直方图技术
含有一个与背景明显对比的物体的图像,其有包含双峰的灰度直方图
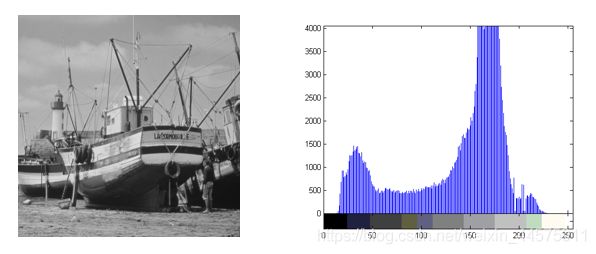
直方图生成代码imhist()
imhist()
pic = imread('coins.png');%读图
%imshow(pic)显示原图
%figure窗体
hist_pic=imhist(pic)%显示直方图
或者
pic=imread('coins.png');
subplot(121),imshow(pic),title('原图');
subplot(122),imhist(pic),title('直方图');
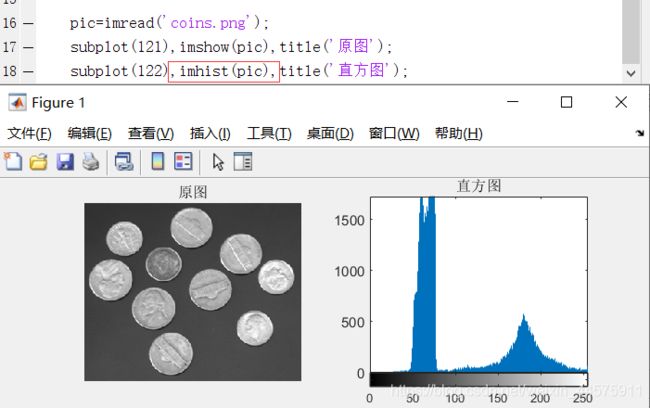
ps : imhist()就直接显示了直方图了,不用加imshow
8.2.3.2最大类间方差法(OTSU)
matlab中函数:graythresh(),ppt上没有,但应该是很常用的
(1)定义
该算法是在灰度直方图的基础上用最小二乘法原理推导出来的,具有统计意义上的最佳分割阈值。
(2)原理
以最佳阈值将图像的灰度直方图分割成两部分,使两部分之间的方差取最大值,即分离性最大。
前提:在图像中前景与背景之间的灰度分布为相互不重叠的前提下实现对两类对象的阈值分割方法。
8.2.3.3 迭代法求阈值
(1)原理
前提:在图像中前景与背景之间的灰度分布为相互不重叠的前提下实现对两类对象的阈值分割方法。
8.2.4分水岭分割算法
(1)分割原理
任何的灰度级图像都可以被看做是一个地形图
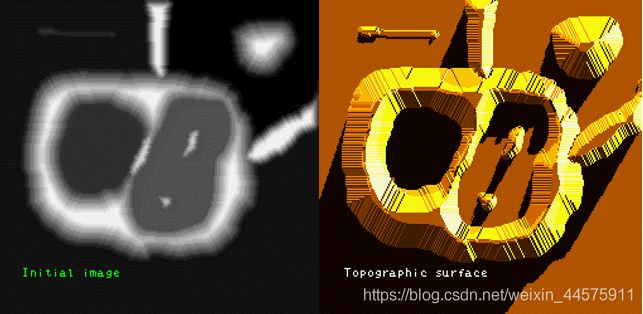
(2)定义
分水岭分割方法应用在图像的梯度,那么集水处在理论上就对应灰度变化最小的区域,而分水岭就对应灰度变化相对最大的区域.
(3)缺点
缺点:由于噪声或者局部不规则而引起”过度分割”

(4)改进
防止“过度分割”
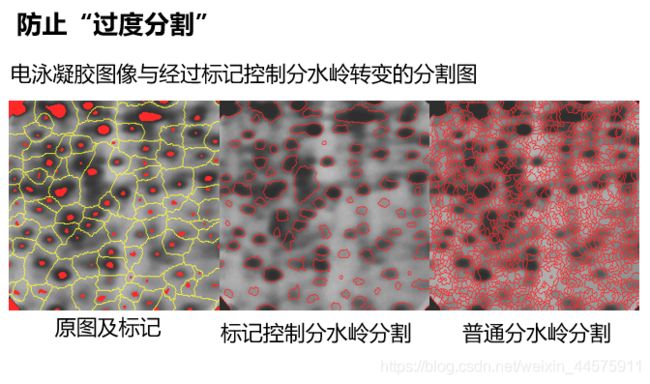
(5)等级分割
(1)通过分分水岭算法,得到一张初始的分割图片
(2)以这些相对高度为基础,再次用分水岭算法
8.3边缘检测和连接
(1)边缘点
确定图像中的物体边界的另一种方法是先检测每个像素和其直接邻域的状态,以决定该像素是否确实处于一个物体的边界上。具有所需特性的像素被标为边缘点。
(2)边缘图像
当图像中各个像素的灰度级用来反映各像素符合边缘像素要求的程度时,这种图像被称为边缘图像。
8.3.1边缘检测
边缘检测算子检查每个像素的邻域并对灰度变化率进行量化,通常也包括方向的确定。有若干种方法可以使用,其中大多数是基于方向导数掩模求卷积的方法。
①Roherts边缘算子
②Sobel边缘算子
③Prewitt边缘算子
④Kirsch边缘算子
8.3.2边缘连接
(1)问题
如果边缘很明显,而且噪声级低,那么可以将边缘图像二值化并将其细化为单像素宽的闭合连通边界图。
然而在非理想条件下,这种边缘图像会有间隙出现,需要加以填充。
(2)解决方法
填充小的间隙可以简单地实现,通过搜索一个以某端点为中心的5×5或更大的邻域,在邻域中找出其它端点并填充上必要的边界像素,从而将它们连接起来。
但是,对具有许多边缘点的复杂场景,这种方法可能会对图像过度分割。为了避免过度的分割,可以规定:两个端点只有在边缘强度和走向相近的情况下才能连接。
①启发式搜索
缺口,两个端点,找出两端点间的全局最优路径(由于启发式搜索技术复杂,未必能找到最优)
②曲线拟合
③Hough变换
8.4区域分割(区域算法利用像素的相似性)
区域分割方法是利用图像的空间性质,考虑了空间关系,分割出来的属于同一区域的像素具有相似的性质。
较为复杂的图像空域采用区域分割技术实现。
8.4.1区域生长法(了解即可)
分为:
(1)简单连接
这是基于单个像素的区域增长法,它从满足的 检测的点(连接核)开始,考察其周围(4邻域或8邻域)的不属于任何一个区域的点,如果其特性符合接收准则,就把它作为同一个区域加以合并,形成连接核,继而检测周围的点,并把符合接入准则的点并入,产生新的核。重复上述过程,直到没有可并入的点时,生产过程结束。
(2)子区合并法
合并过程:
首先:将图像分割成个,大小为的小区域(简
称子区)。
其次:从左上角第一个子区开始,分别计算子
区和相邻子区的灰度统计量,然后做相
似性判定。若两者的灰度分布相似且符
合接收准则。相邻子区并入当前子区,
形成下一轮判定合并时的当前子区。
8.4.1区域分裂合并法(ppt里没有)
8.5二值图像处理
8.5.1数学形态学图像处理
ps:开运算去除细小物体(先腐蚀再膨胀),闭运算连通缝隙(先膨胀再腐蚀)

8.5.1.1概述与集合论基础知识(重点)
(1)数学形态学概述
形态学:一般指生物学中研究动物和植物结构的一个分支
数学形态学(也称图像代数)表示以形态为基础对图像进行分析的数学工具
基本思想:是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的
形态学图像处理的数学基础和所用语言是集合论
形态学图像处理的应用可以简化图像数据,保持它们基本的形状特性,并除去不相干的结构
形态学图像处理的基本运算有4个:膨胀、腐蚀、开操作和闭操作
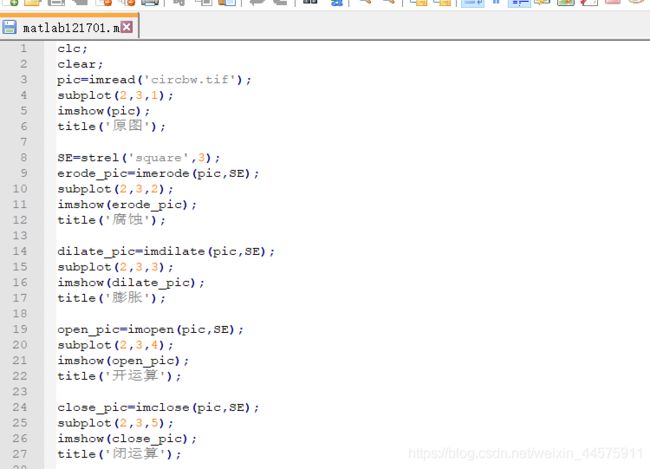
8.5.1.2膨胀
(1)定义
膨胀:使图像扩大
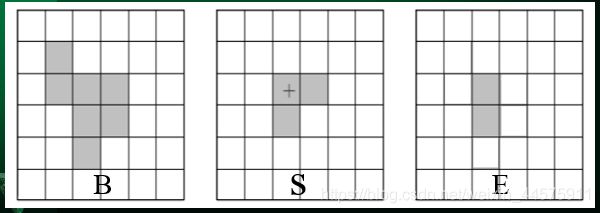
B和S是两个集合,B被S膨胀定义为:
D=B⊕S={ (x, y) | S(x, y) ∩ B ≠ ø}
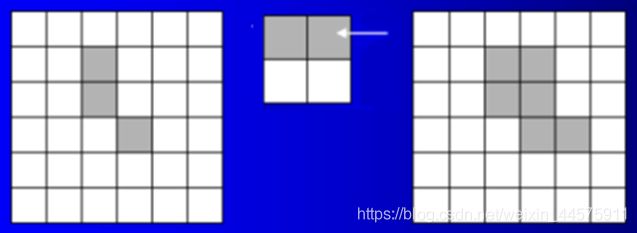
ps:S(x,y)∩B是指当中心点是(x,y)时,结构元素S与原图B交集不为空就是有交集,那这个中心点就要标记为1。
(2)应用
桥接文字裂缝
优点:在一幅二值图像中直接得到结果,对比低通滤波方法。
膨胀的作用:连通近邻的区域;填补目标区域内的小空洞。
8.5.1.3腐蚀
(1)定义
腐蚀:使图像缩小
B和S是两个集合,B被S腐蚀定义为:
E=B Θ S={ (x, y) | S(x, y) ⊆ B }
ps:S(x, y) ⊆ B 是中心点为(x,y)时,S这个结构元素整个都被原图B包含,那就要标记中心点(x,y)为1
(2)应用
腐蚀在数学形态学运算中的作用是消除物体边界点。
如果结构元素取3×3的像素块,腐蚀将使物体的边界沿周边减少一个像素。
腐蚀可以把小于结构元素的物体(毛刺、小凸起)去除,这样选取不同大小的结构元素,就可以在原图像中去掉不同大小的物体。
如果两个物体之间有细小的连通,那么当结构元素足够大时,通过腐蚀运算可以将两个物体分开。

8.5.1.4应用
边界提取、区域填充、连通分量、凸壳、细化、粗化
8.5.2开运算与闭运算
8.5.2.1开运算
(1)定义
先腐蚀后膨胀的过程称为开运算。
(2)作用
消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。
8.5.2.2闭运算
(1)定义
先膨胀后腐蚀的过程称为闭运算。
(2)作用
填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。
8.5.3数学形态学应用算法
8.5.3.1边界提取
用原始图像减去腐蚀结果
(1)定义
β (A)= A−(AΘB)
上式表示:先用B对A腐蚀,然后用A减去腐蚀得到,B是结构元素
8.5.3.2区域填充
(1)定义
定义:设所有非边界(背景)点标记为0,则将1赋给p点开始,
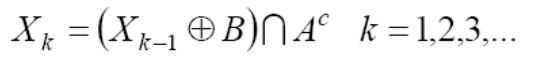
实现目的:从边界内的一个点开始,用1填充整个区域
X0=p,如果Xk=Xk-1,则算法在迭代的第k步结束。Xk和A的并集包含被填充的集合和它的边界
条件膨胀:如果对上述公式的左部不加限制,则上述公式的膨胀将填充整个区域。利用Ac的交集将结果限制在感兴趣区域内,实现条件膨胀。
填充孔洞时,A就是那个与图像四边框连通的背景区域。
pic=imread('circle.jpg');
BW1=im2bw(pic);%二值化
BW2=bwfill(BW1,'holes');%区域填充
imshow(BW2);%上图最右边那个就是效果图
8.5.3.3连通分量的提取
骨架提取(加入再腐蚀会断开,则该点加入骨架)