自旋玻璃（spin glass）、自旋冰（spin ice）和量子自旋液体（quantum spin liquid）（之二）

---

13. 几何阻挫（Geometrical frustration）

在凝聚态物理中，术语几何阻挫（geometrical frustration）（或简称：阻挫（frustration））是指原子倾向于坚持非平凡位置（non-trivial positions）的现象，或者在规则晶格上，原子间冲突力量（每一种力量都倾向于相当简单但不同的结构）导致相当复杂的结构。由于几何形状或力阻挫，在零温度下可能会产生大量不同的基态，并且在较高温度下可能会抑制通常的热排序（thermal ordering）。许多研究的例子是无定形材料（amorphous materials）、玻璃或稀土磁体（dilute magnets）。

阻挫（frustration），或称挫折，在自然界和人类社会中普遍存在，并在一定程度上导致了世界的丰富多彩。物理学中的几何阻挫是指，在某些特定几何结构上的物理系统，无法同时满足所有的竞争相互作用，使得系统具有大量简并的能态。在温度趋近于绝对零度时，经典的热力学涨落已被完全抑制，而量子涨落开始占据主导地位。此时，量子力学原理和几何阻挫的结合可以在固体中产生一些奇异的量子液态。1973年，P. W. Anderson （1977年诺贝尔物理学奖获得者）首先在理论上指出，在三角晶格上反铁磁相互作用的阻挫自旋系统可以存在量子自旋液态（quantum spin liquid）。在此后的几十年中，量子自旋液态吸引了广泛的理论研究，由此发展出了各种理论模型和计算方法，预言了许多新奇的物理性质和物理效应。与此同时，实验物理学家也在努力寻找和探测量子自旋液态。然而，迄今为止，人们仅发现了少数几种可能存在量子自旋液态的候选材料。

Gerard Toulouse 于 1977 年在磁系统的背景下引入了阻挫一词。阻挫的磁系统甚至在以前就已经被研究过了。早期工作包括对最近邻自旋反铁磁耦合的三角形晶格上的 Ising 模型的研究，这项工作由 G. H. Wannier 于 1950 年发表。相关特征出现在具有竞争相互作用（competing interactions）的磁体中，其中在自旋或磁矩对之间存在铁磁和反铁磁耦合，相互作用的类型取决于自旋的分离距离。在这种情况下，可能会产生可公度性（commensurability），例如螺旋自旋排列（helical spin arrangements ），正如最初讨论的那样，特别是 A. Yoshimori，T. A. Kaplan，R. J. Elliott 和其他人，从 1959 年开始，描述稀土金属的实验结果。大约 20 年后，从 1970 年代开始，在自旋玻璃和空间调制磁性超结构的背景下，人们对这种具有阻挫或竞争相互作用的自旋系统重新产生了兴趣。在旋转玻璃中，相互作用中的随机无序加剧了阻挫，实验上，这可能发生在非化学计量磁性合金（non-stoichiometric magnetic alloys）中。详细研究的阻挫自旋模型包括描述自旋玻璃的 Sherrington-Kirkpatrick model ，和描述可公度磁性超结构（commensurability magnetic superstructures）的 ANNNI model。

13.1 磁序（Magnetic ordering）

图 呈三角形排列的反铁磁相互作用自旋

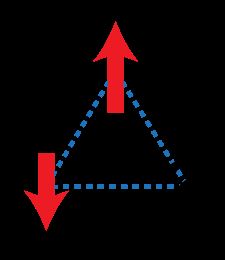
几何阻挫是磁性的一个重要特征，它源于自旋的相对排列。图 1 显示了一个简单的 2D 示例。三个磁性离子位于三角形的角上，它们之间存在反铁磁相互作用；当每个自旋与邻居相反时，能量最小化。一旦前两个自旋反平行对齐，第三个自旋就会阻挫，因为它有两个可能方向，向上和向下，提供相同的能量。第三个自旋不能同时最小化它与其他两个的相互作用。由于每次旋转都会发生这种效应，因此基态是六倍简并（sixfold degenerate）。只有所有自旋同时向上或向下的两种状态具有更多的能量。

图 四面体排列中的反铁磁相互作用自旋

同样在三个维度中，四面体中排列的四个自旋可能会遇到几何阻挫。如果自旋之间存在反铁磁相互作用，则不可能排列自旋以使自旋之间的所有相互作用都是反平行的。如上图，有六个最近邻相互作用，其中四个是反平行的，因此是有利的，但其中两个（在 1 和 2 之间，以及在 3 和 4 之间）是不利的。不可能让所有的交互都有利，系统也会阻挫。

图 沿四面体的易轴（easy axes，即直接朝向或远离四面体中心）自旋

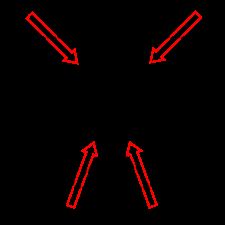
如果自旋以非共线（non-collinear）方式排列，几何阻挫也是可能的。如果我们考虑一个四面体，每个顶点上都有一个自旋指向易轴（即直接朝向或远离四面体中心），那么可以安排四个自旋使得没有净自旋，如上图。这完全等同于在每对自旋之间存在反铁磁相互作用，因此在这种情况下不存在几何挫折。使用这些轴，如果相邻元素之间存在铁磁相互作用，就会出现几何挫折，其中能量通过平行自旋最小化。

最好的安排如下图所示，两个自旋指向中心，两个自旋指向外。净磁矩指向上方，使该方向上的铁磁相互作用最大化，但左右矢量抵消（即反铁磁对齐），向前和向后也是如此。存在三个不同的等效排列，两个自旋和两个自旋，因此基态是三倍简并的（three-fold degenerate）。

图 四面体中阻挫的简单自旋（easy spins）

下面是与阻挫相关的视频：

Video: Frustrated magnetism in solids

13.2 数学定义

数学定义很简单（并且类似于量子色动力学中所谓的威尔逊环（Wilson loop））：例如考虑以下形式的表达式（“总能量”或“哈密顿”）

$$\mathcal{H}=\sum _G-I_{k_{\nu },k_{\mu }}{S}_{k_{\nu }}\cdot S_{k_{\mu }}$$

其中 $G$ 是所考虑的图（graph），而量 $I_{k_{\nu },k\mu }$ 是最近邻之间所谓的“交换能量（exchange energies）”，其（在所考虑的能量单位中）假定值为 $\pm 1$（在数学上，这是一个符号图(signed graph）)，而 $S_{k_{\nu }}\cdot S_{k_{\mu }}$ 是标量或矢量自旋或伪自旋（scalar or vectorial spins or pseudo-spins）的内积。如果图 $G$ 具有二次面或三角形面（quadratic or triangular faces） $P$，则出现所谓的“元格变量（plaquette variables）”$P_W$，即以下类型的“循环积（loop-products）”：

$$P_W=I_{1,2}{I}_{2,3}{I}_{3,4}{I}_{4,1}\text{and}{P}_W=I_{1,2}{I}_{2,3}{I}_{3,1}$$

也称为“阻挫积（frustration products）”。必须对这些积进行求和，对所有元格求和。单个元格的结果是 $+1$ 或 $-1$。在最后提到的例子中，元格“几何上阻挫”。

可以证明，结果具有简单的规范不变性：它不会改变——其他可测量的量也不会改变，例如“总能量” $\mathcal{H}$——即使局部交换积分（locally the exchange integrals）和自旋同时修改如下：

$$I_{i,k}\to {\epsilon }_i{I}_{i,k}{\epsilon }_k,S_i\to {\epsilon }_i{S}_i,S_k\to {\epsilon }_k{S}_k$$
这里数字 ${\epsilon }_i$ 和 ${\epsilon }_k$ 是任意符号（arbitrary signs），即 $+1$ 或 $-1$，因此修改后的结构可能看起来完全随机。

13.3 水冰（water ice）

尽管大多数先前和当前关于阻挫的研究都集中在自旋系统上，但这种现象首先是在普通冰中研究的。1936 年 Giauque 和 Stout 发表了“水的熵和热力学第三定律。冰的热容量从 $15\mathrm{K}$ 到 $273\mathrm{K}$（“The Entropy of Water and the Third Law of Thermodynamics. Heat Capacity of Ice from $15\mathrm{K}$ to $273\mathrm{K}$”），报告了热量计（calorimeter）测量水通过冻结和汽化过渡到高温气相的过程。熵是通过对热容积分并加上潜热贡献来计算的；使用德拜当时最近推导出的公式将低温测量值外推为零。将所得熵 $S_1=44.28cal/(\mathrm{K}\cdot \mathrm{mol})=185.3J/(\mathrm{mol}\cdot \mathrm{K})$ 与理想气体统计力学的理论结果 $S_2=45.10cal/(\mathrm{K}\cdot \mathrm{mol})=188.7J/(\mathrm{mol}\cdot \mathrm{K})$ 进行比较。这两个值相差 $S_0=0.82\pm 0.05cal/(\mathrm{K}\cdot \mathrm{mol})=3.4J/(\mathrm{mol}\cdot \mathrm{K})$。1935 年，Linus Pauling 将这一结果解释为一个极好的近似值，他表明冰在零温度下具有有限的熵（估计为 $0.81cal/(\mathrm{K}\cdot \mathrm{mol})$ 或 $3.4J/(\mathrm{mol}\cdot \mathrm{K})$），原因是冰中质子固有的构型无序。

图 水冰分子示意图

在六方或立方冰相中，氧离子形成四面体结构，O-O 键长为 $2.76\mathring{\mathrm{A}}$（$276\mathrm{pm}$），而 O-H 键长仅为 $0.96\mathring{\mathrm{A}}$（$96\mathrm{pm}$）。如上图所示，每个氧（白色）离子被四个氢离子（黑色）包围，每个氢离子被两个氧离子包围。保持内部 ${\mathrm{H}}_2\mathrm{O}$ 分子结构，质子的最小能量位置不是半两个相邻的氧离子之间的方式。氢在 O-O 键线上可能占据两个等效位置，一个远位置和一个近位置。因此，一条规则导致基态配置的质子位置阻挫：对于每个氧离子，两个相邻的质子必须位于远处，其中两个位于近处，即所谓的“冰规则（ice rule）”。Pauling 提出，冰的开放四面体结构提供了许多满足冰规则的等效状态。

Pauling 继续以下列方式计算构型熵（configurational entropy）：考虑一摩尔冰，由 $N{\mathrm{O}}^{2-}$ 和 $2N$ 质子组成。每个 O-O 键都有两个质子位置，导致 $2^{2N}$ 种可能的构型。然而，在与每种氧相关的 16 种可能构型中，只有 6 种在能量上是有利的，从而保持了 ${\mathrm{H}}_2\mathrm{O}$ 分子的约束。然后，基态可以取的数字的上限估计为 $\Omega <2^{2N}(\frac{6}{16}{)}^N$。相应地，构型熵 $S_0=k_{\mathrm{B}}\ln (\Omega )=N{k}_{\mathrm{B}}\ln (\frac{3}{2})=0.81cal/(\mathrm{K}\cdot \mathrm{mol})=3.4J/(\mathrm{mol}\cdot \mathrm{K})$ 与 Giauque 和 Stout 测量的缺失熵（missing entropy）惊人地一致。

尽管鲍林的计算忽略了质子数的全局约束和纤锌矿晶格（Wurtzite lattice）上的闭环（closed loops）引起的局部约束，但随后证明该估计具有极好的准确性。

13.4 Pauling’s model 的扩展：广义的阻挫

自旋冰模型只是阻挫系统的一个分支。最初引入阻挫这个词是为了描述一个系统无法同时最小化其组份之间的竞争相互作用能量。一般来说，阻挫是由由于位点无序引起的竞争相互作用引起的（另见 Villain model）或由晶格结构引起，例如三角形、面心立方（fcc）、六方密排、四面体、烧绿石和具有反铁磁相互作用的 kagome 晶格（triangular, face-centered cubic (fcc), hexagonal-close-packed, tetrahedron, pyrochlore and kagome lattices with antiferromagnetic interaction）。所以阻挫分为两类：第一类对应于自旋玻璃，既有结构无序，又有自旋阻挫；第二个是有序晶格结构的几何阻挫和自旋阻挫。在 RKKY 模型 的框架内理解自旋玻璃的阻挫，其中铁磁或反铁磁的相互作用特性取决于两个磁性离子的距离。由于自旋玻璃中的晶格无序，一个感兴趣的自旋及其最近的邻居可能处于不同的距离并具有不同的相互作用特性，从而导致自旋的不同优选排列。

13.5 人工几何阻挫铁磁体

在光刻技术的帮助下，可以制造亚微米大小的磁岛（magnetic islands），其几何排布再现了自然产生的自旋冰材料中的阻挫。最近 R. F. Wang 等人。报道发现了一种由光刻制造的单畴铁磁岛阵列组成的人造几何阻挫磁体。这些岛屿是手动排列的，以创建一个二维模拟来自旋冰。有序“自旋”岛的磁矩用磁力显微镜 (MFM) 成像，然后彻底研究了阻挫的局部调节。在他们之前对阻挫磁体的方晶格的研究中，他们观察到冰状的短程相关性和长程相关性的缺失，就像在低温下的自旋冰中一样。这些结果巩固了未知的基础，在这些基础上，可以通过这些人造几何阻挫磁体对阻挫的真实物理学进行可视化和建模，有助于进一步的研究。

当使用磁光克尔效应（Magneto-Optical Kerr Effect）研究它们对外部场的全局响应时，这些人工阻挫的铁磁体可以表现出独特的磁性。特别是，发现方形晶格矫顽力的非单调角度依赖性与人造自旋冰系统中的无序有关。

13.6 没有晶格的几何阻挫

另一种类型的几何挫折来自局部秩序的传播。凝聚态物理学家面临的一个主要问题是解释固体的稳定性。

有时可以建立一些化学性质的局部规则，这些规则导致低能量构型，因此支配结构和化学秩序。通常情况并非如此，并且通常由局部作用决定的局部秩序不能自由传播，从而导致几何阻挫。所有这些系统的一个共同特点是，即使有简单的局部规则，它们也呈现出大量、通常是复杂的结构。几何阻挫在凝聚态物质领域中发挥作用，从团簇和无定形固体到复杂流体。

解决这些问题的一般方法遵循两个步骤。首先，通过考虑空间曲率，放宽了完美空间填充的约束。在这个弯曲的空间中定义了一个理想的、不受阻挫的结构。然后，对这个理想模板应用特定的变形（distortions），以便将其嵌入到三维欧几里得空间中。最终的结构是有序区域的混合，其中局部顺序类似于模板的局部顺序，以及嵌入产生的缺陷。在可能的缺陷中，旋错（disclinations）起着重要作用。

13.6.1 简单的二维示例

图 用五边形平铺平面是不可能的，但可以在五边形十二面体形式的球体上实现，如准晶体所示。

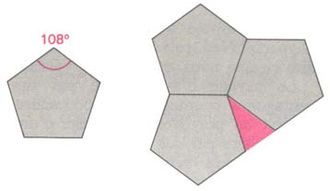
二维例子有助于理解局部规则与大几何之间竞争的起源。首先考虑在平面上排列相同的圆盘（假设二维金属的模型）；我们假设圆盘之间的相互作用是各向同性的，并且局部倾向于以最密集的方式排列圆盘。三个磁盘的最佳排列通常是一个等边三角形，磁盘中心位于三角形顶点。因此，对长程结构的研究可以简化为具有等边三角形的平面平铺。一个众所周知的解决方案是由在局部和全局规则之间完全兼容的三角形平铺提供的：系统被称为“不阻挫的”。

但是现在，当原子位于正五边形的顶点时，相互作用能应该是最低的。试图在远距离传播这些五边形的堆积共享边（原子键）和顶点（原子）是不可能的。这是因为不可能用正五边形平铺平面，仅仅因为五边形的顶角不整除 $2\pi$。三个这样的五边形可以很容易地安装在一个共同的顶点上，但两个边之间仍然存在间隙。正是这种差异被称为“几何阻挫”。有一种方法可以克服这个困难。让要平铺的表面没有任何预设的拓扑结构，让我们在严格应用局部作用规则的情况下构建平铺。在这个简单的例子中，我们观察到曲面继承了球体的拓扑结构，因此接受了曲率。最终的结构，这里是五边形十二面体，允许五边形顺序的完美传播。它被称为所考虑结构的“理想”（无缺陷）模型。

13.6.2 致密结构和四面体堆积

图 四面体堆积：四面体的二面角与 2π 不可公度； 因此，在具有共同边的五个四面体堆积的两个面之间保留了一个孔。 由 20 个具有公共顶点的四面体组成，使得 12 个外部顶点形成一个不规则的二十面体

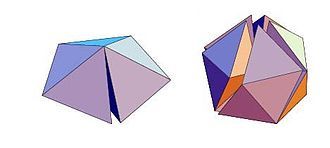
金属的稳定性是固态物理学中长期存在的问题，只有在量子力学框架中适当考虑带正电离子与价电子和传导电子之间的相互作用才能理解。然而，可以使用非常简化的金属键合图，并且仅保持各向同性类型的相互作用，从而产生可以表示为密堆积球体的结构。实际上，晶体简单金属结构通常是密堆积面心立方（fcc）或六方密堆积（hcp）晶格。在某种程度上，无定形金属和准晶体也可以通过球体的密堆积来模拟。局部原子顺序由四面体的紧密堆积很好地模拟，导致不完美的二十面体顺序。

正四面体是四个相等球体堆积的最密集构型。因此，硬球的密集随机堆积问题可以映射到四面体堆积问题上。尝试打包乒乓球以仅形成四面体构型是一项实际练习。一开始是四个球排列成一个完美的四面体，并尝试添加新的球体，同时形成新的四面体。下一个解决方案，有五个球，通常是两个共享一个共同面的四面体；请注意，已经使用此解决方案，包含单个四面体孔的 fcc 结构不会显示这种构型（四面体共享边，而不是面）。用六个球，构建了三个正四面体，并且该簇与所有紧凑的晶体结构（fcc 和 hcp）不相容。添加第七个球体得到一个新的簇，由两个相互接触的“轴向”球和另外五个接触后两个球的“轴向”球组成，外部形状几乎是规则的五边形双锥体。然而，我们现在面临一个真正的堆积问题，类似于上面遇到的二维五边形平铺问题。四面体的二面角与 $2\pi$ 不可公度；因此，在相邻四面体的两个面之间留有一个洞。因此，欧几里得空间 ${\mathbb{R}}^3$ 的完美平铺对于正四面体是不可能的。阻挫具有拓扑特征：如果我们强制规定恒定数量的四面体（这里是五个）共享一个共同的边，就不可能用四面体填充欧几里得空间，甚至是很大的变形都不行。

下一步至关重要：通过允许空间中的曲率来寻找不受阻挫的结构，以便局部配置在整个空间中相同且没有缺陷地传播。

13.6.3 四面体的规则堆积：多面体 {3,3,5}

图 600-cells：多胞体（polytope） {3,3,5}

二十个不规则四面体具有一个共同的顶点，使得十二个外部顶点形成一个正二十面体。实际上，二十面体边长略长于外接球半径 $r(l\approx 1.05r)$。如果空间不是欧几里得，而是球面，则存在正四面体的解。它是多面体 {3,3,5}，使用 Schläfli 表示法，也称为 600-cell。

有 120 个顶点都属于超球面（hypersphere） $S^3$，如果边是单位长度，其半径等于黄金比例（$\phi =\frac{1+\sqrt{5}}{2}$）。六百个 cells 是规则的四面体，由五个围绕一个共同边和二十个围绕一个共同顶点组成。这种结构称为多胞形（polytope ）（参见 Coxeter），它是包含多边形和多面体的系列中更高维度的通用名称。即使这种结构嵌入在四个维度中，它也被认为是一个三维（弯曲的）流形。这一点在概念上很重要，原因如下。曲面空间中引入的理想模型是三维曲面模板。它们在本地看起来像三维欧几里得模型。因此，如果原子位于其顶点上，则由四面体平铺的 {3,3,5} 多面体提供了非常密集的原子结构。因此，它自然地被用作非晶态金属（amorphous metals）的模板，但不应忘记它是以连续理想化为代价的。

14. 自旋冰（Spin ice）

图 冰中氢原子（黑色圆圈）围绕氧原子（空心圆圈）的排列。 两个氢原子（底部的）靠近中心的氧原子，而其中的两个（顶部的）离另外两个（左上和右上）氧原子越来越近。

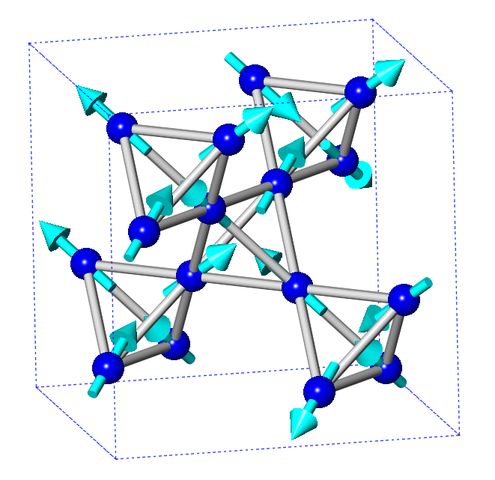
自旋冰是一种磁性物质，没有单一的最小能量状态。受阻挫相互作用的影响，它以磁矩（即“自旋”）作为基本自由度。就其性质而言，这些相互作用可防止磁矩在其方向上表现出周期性模式，直至温度远低于所述相互作用设定的能量量级（energy scale）。自旋冰表现出低温特性，特别是残余熵（residual entropy），与常见的结晶水冰密切相关。自旋冰中磁矩的方向类似于常规水冰中氢原子（更准确地说是电离氢或质子）的位置组织结构（见上图）。

图 自旋冰分子示意图

在自旋冰中发现了与水冰的退化在数学上类似的情况。一种常见的自旋冰结构如上图所示，采用立方烧绿石结构，四个角各有一个磁性原子或离子。由于材料中的强晶体场（crystal field），每个磁性离子都可以用一个具有很大矩的伊辛基态双峰（Ising ground state doublet with a large moment）来表示。这表明伊辛自旋（Ising spins）位于共享角（corner-sharing）的四面体晶格上，自旋沿局部量化轴（quantization axis，<111> cubic axes）固定，与将每个四面体顶点连接到中心的线重合。每个四面体单元必须有两个自旋指向内部和两个指向外部，以最小化能量。目前，自旋冰模型已通过真实材料近似实现，其中最著名的是具有这种特性的最突出的化合物是钛酸镝 (dysprosium titanate，$\mathrm{D}{\mathrm{y}}_2\mathrm{T}{\mathrm{i}}_2{\mathrm{O}}_7$) 和钛酸钬 (holmium titanate，稀土烧绿石（rare earth pyrochlores），$\mathrm{H}{\mathrm{o}}_2\mathrm{T}{\mathrm{i}}_2{\mathrm{O}}_7$)。这些材料在低温下都显示出非零残余熵。

实验已经发现了这些材料中存在无限制磁单极子（deconfined magnetic monopoles）的证据，具有类似于假定存在于真空中的假设磁单极子的特性。

2022 年，Paul Scherrer 研究所的瑞士研究人员实现了一种人造 kagome 自旋冰，可用于低功耗的新型高速计算机。

14.1 具体描述

图 角连接四面体烧绿石晶格的一部分。磁性离子（深蓝色球体）位于顶点连接的四面体（corner-linked tetrahedra）网络上。不显示形成烧绿石晶体结构的其他原子（例如 Ti 和 O）。整个晶格的磁矩（浅蓝色箭头）服从二进二出自旋冰规则（two-in, two out spin ice rule）。该系统因此处于自旋冰状态。

1935 年，Linus Pauling 指出，即使绝对为零，水冰中的氢原子仍会保持无序状态。 也就是说，即使冷却到零温度，预计水冰也会具有残余熵，即内在随机性（intrinsic randomness）。 这是因为普通水冰的六方晶体结构包含氧原子和四个相邻的氢原子。 在冰中，对于每个氧原子，有两个相邻的氢原子靠近（形成传统的 ${\mathrm{H}}_2\mathrm{O}$ 分子），两个更远（作为两个相邻水分子的氢原子）。 鲍林指出，符合“两近两远”冰规则的配置数量随着系统大小呈指数增长，因此，预计冰的零温度熵将是广泛的。鲍林的发现得到了比热测量的证实，尽管纯净的水冰晶体特别难以制造。

自旋冰是由规则的角连接四面体磁性离子组成的材料，每个四面体都有一个非零磁矩（non-zero magnetic moment），通常缩写为“自旋（spin）”，在其低能状态下，对每个四面体构成晶体结构，必须满足“二进二出”规则（two-in, two out spin ice rule）。这与水冰中的两近两远规则（two-near, two far rule）高度相似。正如鲍林表明冰规则导致水冰中的广延熵（extensive entropy）一样，自旋冰系统中的二进二出规则也是如此——这些规则与水冰表现出相同的剩余熵特性。尽管如此，根据具体的自旋冰材料，通常比水冰晶体更容易制造大的自旋冰材料单晶。此外，在自旋冰系统中易于诱导磁矩与外部磁场的相互作用使得自旋冰比水冰更适合探索残余熵如何受到外部影响的影响。

虽然 Philip Anderson 在 1956 年已经注意到在角共享四面体（corner-shared tetrahedra，pyrochlore（烧绿石））晶格上阻挫的伊辛反铁磁体问题与鲍林的水冰问题之间的联系，但真正的自旋冰材料直到 40 年后才被发现。第一种被确定为自旋冰的材料是烧绿石 钛酸镝 (dysprosium titanate，$\mathrm{D}{\mathrm{y}}_2\mathrm{T}{\mathrm{i}}_2{\mathrm{O}}_7$) 和钛酸钬 (holmium titanate，$\mathrm{H}{\mathrm{o}}_2\mathrm{T}{\mathrm{i}}_2{\mathrm{O}}_7$)。此外，据报道，令人信服的证据表明 $\mathrm{D}{\mathrm{y}}_2\mathrm{S}{\mathrm{n}}_2{\mathrm{O}}_7$（锡酸镝，dysprosium stannate）和 $\mathrm{H}{\mathrm{o}}_2\mathrm{S}{\mathrm{n}}_2{\mathrm{O}}_7$（锡酸钬，holmium stannate）是自旋冰。这四种化合物属于稀土烧绿石氧化物家族。$\mathrm{CdE}{\mathrm{r}}_2\mathrm{S}{\mathrm{e}}_4$ 是一种尖晶石，其中磁性 $E{r}^{3+}$ 离子位于角连接的四面体上，也显示出自旋冰行为。

自旋冰材料的特点是磁离子矩的方向随机无序，即使材料处于非常低的温度下也是如此。交流（AC）磁化率测量发现了磁矩动态冻结的证据，因为温度稍微低于比热显示最大值的温度。热容量的广泛最大值不对应于相变。相反，在 $\mathrm{D}{\mathrm{y}}_2\mathrm{T}{\mathrm{i}}_2{\mathrm{O}}_7$ 中出现最大值的温度约为 $1\mathrm{K}$，这表明四面体的数量发生了快速变化，其中违反了二进二出规则。违反规则的四面体是上述单极子所在的位置。

14.2 自旋冰和磁单极子

图 考虑自旋冰内单个四面体的磁矩方向（浅蓝色箭头）。这里，磁矩遵循二进二出规则：有尽可能多的“ 磁化场”进入四面体（底部两个箭头），同时也有出去（顶部两个箭头）。相应的磁化场具有零散度。 因此，四面体内部没有磁化的汇或源，或没有单极子。如果热波动导致底部两个磁矩之一从“输入”翻转到“输出”，则一个将具有 1 进 3 出配置；因此磁化的“流出”，因此是正的发散，可以分配给带正电的单极电荷 +Q。翻转两个底部磁矩将给出 0 进，4 出配置，最大可能的“流出” "（即发散）磁化，因此，相关的单极电荷 +2Q。

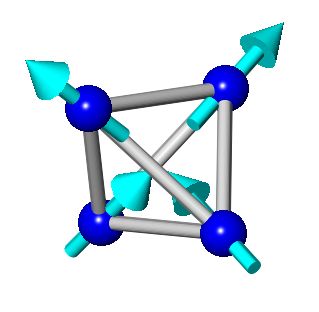
自旋冰是几何阻挫的磁系统。虽然阻挫通常与通过反铁磁交换相互作用耦合的磁矩的三角形或四面体排列有关，如在安德森的伊辛模型中，自旋冰是阻挫的铁磁体。正是来自晶体场的非常强的局部磁各向异性迫使磁矩指向四面体内部或外部，这使得自旋冰中的铁磁相互作用阻挫。最重要的是，导致自旋冰现象学的阻挫和相应的二进二出规则的是长程静磁偶极-偶极相互作用，而不是最近邻交换。

对于处于二进二出状态的四面体，磁化场是无发散的；进入四面体的“磁化强度”与离开四面体的“磁化强度”一样多。在这种无发散的情况下，该场不存在源或汇。根据高斯定理（也称为 Ostrogradsky’s theorem），场的非零散度是由一个称为“电荷（charge）”的实数引起的，并且可以用一个实数来表征。在自旋冰的背景下，这种违反二进二出磁矩方向规则的电荷是上述单极子。

2009 年秋季，研究人员报告了对类似于自旋冰中预测的单极子的低能准粒子的实验观察。在 $0.6-2.0\mathrm{K}$ 的温度范围内检查了钛酸镝自旋冰候选的单晶。使用中子散射，磁矩显示在自旋冰材料中排列成类似于狄拉克弦（Dirac strings）的交织管状束（interwoven tube-like bundles）。在每个管子末端形成的缺陷处，磁场看起来像一个单极子。使用外加磁场，研究人员能够控制这些弦的密度和方向。还介绍了根据这些准粒子的有效气体来描述材料的热容量。

在镝和钛酸钬自旋冰化合物中，磁单极子的有效电荷 $Q$ 约为 $Q=5{\mu }_{\mathrm{B}}{\mathring{\mathrm{A}}}^{-1}$（玻尔磁子每埃）。自旋冰的基本磁性成分是磁偶极子，因此单极子的出现是 fractionalization 现象的一个例子。

磁性材料中原子磁矩的微观起源是量子力学；普朗克常数明确地进入定义电子磁矩的方程，以及它的电荷和质量。然而，钛酸镝和钛酸钬自旋冰材料中的磁矩在自旋的实验相关和合理可及的温度范围（$0.05\mathrm{K}$ 和 $2\mathrm{K}$ 之间）内被经典统计力学而非量子统计力学有效描述。冰现象显现出来。尽管这两种化合物中量子效应的弱点是相当不寻常的，但据信这是可以理解的。目前人们对寻找量子自旋冰很感兴趣，在这些材料中，现在需要量子力学定律来描述磁矩的行为。除了镝（Dy）和钬（Ho）之外的磁性离子需要产生量子自旋冰，镨（Pr）、铽（Tb）和镱（Yb）是可能的候选者。对量子自旋冰感兴趣的一个原因是相信这些系统可能含有量子自旋液体，一种磁矩继续摆动（波动）到绝对零温度的物质状态。描述量子自旋冰的低温和低能特性的理论类似于真空量子电动力学或 QED。这构成了涌现思想的一个例子。

15. 量子自旋液体（Quantum spin liquid）

在凝聚态物理中，量子自旋液体（quantum spin liquid，QSL）是一种物质相，可以通过某些磁性材料中的量子自旋相互作用而形成。 量子自旋液体通常具有长程量子纠缠、分形激发（fractionalized excitation）和不存在普通磁序的特征。

量子自旋液态首先由物理学家 Phil Anderson 于 1973 年提出，作为三角形晶格上自旋系统的基态，该系统与最近的邻居发生反铁磁相互作用，即相邻的自旋寻求在相反的方向上对齐。1987 年，Anderson 提出了一种理论，该理论根据无序的自旋液体状态来描述高温超导性，量子自旋液体引起了学术界进一步的兴趣。

15.1 基本属性

Frustrated magnetism

视频：阻挫磁性产生的自旋液体示例

最简单的磁相是顺磁体（paramagnet），其中每个单独的自旋都独立于其他自旋，就像理想气体中的原子一样。这种高度无序的相是高温下磁体的一般状态，其中热涨落占主导地位。冷却后，自旋通常会进入铁磁体（或反铁磁体）相。在这个阶段，自旋之间的相互作用使它们排列成大规模的图案，例如域（domains）、条纹（stripes）或棋盘（checkerboards）。这些长程模式被称为“磁序（magnetic order）”，类似于由许多固体形成的规则晶体结构。

量子自旋液体为这种典型行为提供了一种戏剧性的替代方案。与铁磁自旋状态相比，这种状态的一个直观描述是无序自旋的“液体”，与结晶冰相比，液态水处于无序状态的方式非常相似。然而，与其他无序状态不同，量子自旋液态将其无序状态保持在非常低的温度下。量子自旋液体更现代的表征涉及它们的拓扑序（topological order）、长程量子纠缠特性（long-range quantum entanglement properties）、和任意子激发（anyon excitations）。

15.2 自旋子（Spinon）

Spinons 是三种准粒子（quasiparticles）之一，连同全子（holons）和轨道子（orbitons），当在接近绝对零的温度下时，由固体中的电子能够在自旋电荷分离（spin-charge separation）过程中分裂而成。电子在理论上总是可以被认为是三者的束缚态，自旋子携带电子的自旋，轨道子携带轨道位置，全子携带电荷，但在某些条件下，它们可以表现为独立的准粒子。

自旋子一词经常用于在量子自旋液体和强相关量子自旋液体的框架内讨论实验事实。

15.2.1 概述

具有相同电荷的电子相互排斥。结果，为了在极其拥挤的环境中相互超越，他们不得不改变自己的行为。剑桥大学和英国伯明翰大学于 2009 年 7 月发表的研究表明，电子可以通过量子隧穿从金属表面跳到相近位置的量子线上，这样做后，将分离成两个准粒子，命名为的自旋子和全子。

Van den Brink、Khomskii 和 Sawatzky 在 1997-1998 年对轨道子进行了理论上的预测。在 2011 年 9 月发给出版商的论文中报告了它作为一个单独的准粒子的实验观察结果。该研究指出，通过向一维铜酸锶样品中的单个电子发射一束 X 射线光子，这会将电子激发到更高的轨道，导致光束在此过程中损失一部分能量。这样做时，电子将被分离成一个自旋子和一个轨道子。这可以通过观察碰撞前后 X 射线的能量和动量来追踪。

15.3 例子

几种物理模型具有无序的基态，可以描述为量子自旋液体。

15.3.1 阻挫的磁矩

图 在三角形上，阻挫的伊辛自旋。

如果存在不能同时满足的相互竞争的交换相互作用（exchange interactions），则局部自旋会受到阻挫，从而导致系统基态的大量退化（degeneracy）。反铁磁相互作用的伊辛自旋三角形（意味着自旋的唯一可能方向是“向上”或“向下”）是一个简单的阻挫示例。在基态，两个自旋可以是反平行的，但第三个不能。这导致基态自旋的可能方向（在这种情况下为六个）增加，增强了涨落，从而抑制了磁有序。

15.3.2 共振价键（Resonating valence bonds，RVB）

图 价键固体（valence bond solid）。这些键形成一种特定的模式，由成对的纠缠自旋组成。

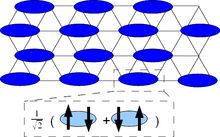
为了建立没有磁矩的基态，可以使用价键态（valence bond states），其中两个电子自旋由于反铁磁相互作用而形成自旋 0 单重态（singlet）。如果系统中的每个自旋都像这样被束缚，那么整个系统的状态也是自旋为 0 并且是非磁性的。形成键的两个自旋最大程度地纠缠在一起，而不与其他自旋纠缠在一起。如果所有自旋都分布在某些局部静态键（localized static bonds）上，则称为价键固体（valence bond solid，VBS）。

VBS 与自旋液体仍有两点区别：首先，通过以某种方式对键进行排序，晶格对称性通常会被破坏，而自旋液体则不是这种情况。其次，这种基态缺乏长程纠缠。为了实现这一点，必须允许价键的量子力学涨落（quantum mechanical fluctuation），这样会导致基态由许多不同的自旋分配叠加（superposition of many different partitionings of spins）成价键组成。如果分配（partitionings）是均匀分布的（具有相同的量子幅度），则不存在任何特定分区（“价键液体（valence bond liquid）”）的偏好。这种基态波函数由 P. W. Anderson 在 1973 年提出作为自旋液体的基态，称为共振价键（resonating calence bond，RVB）态。这些状态具有极大的理论意义，因为它们被提议在高温超导体物理学中发挥关键作用。

图 在 RVB 状态下，一种可能的短程自旋配对（short-range pairing of spins）。 图 远程配对旋转（long-range pairing of spins）。

15.3.2.1 激发（Excitations）

图 自旋子（spinon）在自旋液体中移动。

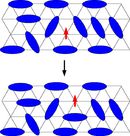
价键不必仅由最近邻形成，并且它们的分布在不同材料中可能不同。具有较大贡献的长程价键的基态具有更多的低能自旋激发（low-energy spin excitations），因为这些价键更容易断裂。断裂时，它们形成两个自由自旋（two free spins）。其他激发重新排列价键，即使对于短程键也会导致低能量激发。自旋液体非常特别的一点是它们支持奇异的激发（exotic excitations），这意味着具有分数量子数（fractional quantum numbers）的激发。一个突出的例子是带电中性并携带自旋 $S=1/2$ 的自旋子（spinons）的激发。在自旋液体中，如果一个自旋没有在价键中配对，则会产生一个自旋子。它可以通过以低能量代价重新排列附近的价键来移动。

15.3.2.2 （稳定） RVB 状态的实现

使用 RVB 图片，对方形晶格上的 RVB 状态的第一次讨论仅考虑连接不同子晶格的最近邻键。构建的 RVB 状态是所有最近邻键配置（configrations）的等幅叠加（equal amplitude superposition）。这种 RVB 状态被认为包含涌现的无间隙（gapless）$U(1)$ 规范场，这可能会限制自旋子等。因此，方格上的等幅最近邻 RVB 状态是不稳定的并且不对应到量子自旋相。它可以描述两个稳定相之间的临界相变点。RVB 状态的一个版本，它是稳定的并且包含无限制（deconfined）的自旋子，是手性自旋状态。后来，提出了另一种具有无限制旋子的稳定 RVB 状态，即 Z2 自旋液体，实现了最简单的拓扑序 - Z2 拓扑序。手性自旋态和 Z2 自旋液态都具有连接相同亚晶​​格（sub-lattice）的长 RVB 键。在手性自旋状态下，不同的键构型可以具有复振幅，而在 Z2 自旋液态下，不同的键构型只有实振幅。三角晶格上的 RVB 状态也实现了 Z2 自旋液体，其中不同的键构型只有真实的幅度。复曲面代码模型（toric code）是 Z2 自旋液体（和 Z2 拓扑序）的另一种实现，它明确打破了自旋旋转对称性并且完全可溶。

15.4 实验特征和探针

由于没有单一的实验特征可以将材料识别为自旋液体，因此必须进行几个实验以获得有关表征自旋液体的不同特性的信息。

15.4.1 磁化率

在高温、经典顺磁相中，磁化率由 Curie–Weiss law 给出：

$$\chi \sim \frac{C}{T-{\Theta }_{CW}}$$

将实验数据拟合到这个方程确定了一个现象学的 Curie-Weiss 温度，${\Theta }_{CW}$。还有第二个温度，$T_c$，材料中的磁序开始发展，如 $\chi (T)$。这些的比率称为阻挫参数（frustration parameter）：

$$f=\frac{|{\Theta }_{cw}|}{T_c}$$

在经典的反铁磁体中，两个温度应该重合并给出 $f=1$。理想的量子自旋液体在任何温度 $(T_c=0)$ 都不会产生磁序，因此会有一个发散的阻挫参数 $f\to \infty$。因此，较大的值 $f>100$ 是可能的自旋液相的良好标识。下表列出了一些具有不同晶格结构及其 Curie-Weiss 温度的阻挫材料。所有这些都是提议的旋转液体候选者。

Material	Lattice	${\Theta }_{cw}[\mathrm{K}]$
$\kappa -(\mathrm{BEDT}-\mathrm{TTF}{)}_2\mathrm{C}{\mathrm{u}}_2(\mathrm{CN}{)}_3$	anisotropic triangular	-375
$\mathrm{ZnC}{\mathrm{u}}_3(\mathrm{OH}{)}_6\mathrm{C}{\mathrm{l}}_2$ (herbertsmithite)	Kagome	-241
$\mathrm{BaC}{\mathrm{u}}_3{\mathrm{V}}_2{\mathrm{O}}_8(\mathrm{OH}{)}_2$ (vesignieite)	Kagome
$\mathrm{N}{\mathrm{a}}_4\mathrm{I}{\mathrm{r}}_3{\mathrm{O}}_8$	Hyperkagome	-650
$\mathrm{PbCuT}{\mathrm{e}}_2{\mathrm{O}}_6$	Hyperkagome	-22
$\mathrm{Cu}-(1,3-\mathrm{benzenedicarboxylate})$	Kagome	-33
$\mathrm{R}{\mathrm{b}}_2\mathrm{C}{\mathrm{u}}_3\mathrm{Sn}{\mathrm{F}}_{12}$	Kagome
$1T-\mathrm{Ta}{\mathrm{S}}_2$	Triangular

15.4.2 其他

不存在磁有序的最直接证据之一是 NMR 或 μSR 实验。如果存在局部磁场，则可以测量核或介子自旋会受到的影响。对 $\kappa -(\mathrm{BEDT}-\mathrm{TTF}{)}_2\mathrm{C}{\mathrm{u}}_2(\mathrm{CN}{)}_3$ 的 H-NMR 测量没有显示出低至 $32\mathrm{mK}$ 的磁有序迹象，这比在该化合物的相邻自旋之间的耦合常数 $J\approx 250\mathrm{K}$ 小四个数量级。进一步的研究包括：

• 比热测量（specific heat measurements）提供了有关状态的低能量密度的信息，可以与理论模型进行比较。
• 热传输测量（thermal transport measurements）可以确定激发是局部的还是流动的（itinerant）。
• 中子散射（neutron scattering）提供有关激发和相关性（例如自旋子）性质的信息。
• 反射率测量（reflectance measurements）可以发现自旋子，自旋子通过涌现规范场（emergent gauge fields）耦合到电磁场，从而产生幂律光导率（power-law optical conductivity）。

15.5 候选材料

15.5.1 RVB 型

氯铜酸铯 $\mathrm{C}{\mathrm{s}}_2\mathrm{CuC}{\mathrm{l}}_4$（一种三角形晶格上的 spin-1/2 反铁磁体）的中子散射测量显示出漫散射。这归因于由 2D RVB 状态产生的自旋子。后来的理论工作对这张图像提出了挑战，认为所有的实验结果都是一维自旋子局限于单个链的结果。

之后，2003 年 Kanoda 的小组在 organic Mott insulator（$\kappa -(\mathrm{BEDT}-\mathrm{TTF}{)}_2\mathrm{C}{\mathrm{u}}_2(\mathrm{CN}{)}_3$) 中观察到了它。它可能对应于具有自旋费米面的无间隙自旋液体（即所谓的均匀 RVB 态）。这种有机量子自旋液体化合物的特殊相图首先使用介子自旋光谱进行了彻底的绘制。

15.5.2 Herbertsmithite

图 Herbertsmithite，一种基态被证明具有 QSL 行为的矿物

Herbertsmithite 是研究最广泛的 QSL 候选材料之一。 它是一种化学成分为 $\mathrm{ZnC}{\mathrm{u}}_3(\mathrm{OH}{)}_6\mathrm{C}{\mathrm{l}}_2$，晶体结构为菱面体（rhombohedral）的矿物。值得注意的是，这种结构中的铜离子形成了堆叠的二维 kagome lattices 层。此外，氧键上的超交换（superexchange）在单层内的 $S=1/2$ 铜自旋之间产生了强烈的反铁磁相互作用，而层间的耦合可以忽略不计。因此，它很好地实现了 kagome 晶格上的反铁磁自旋 1/2 海森堡模型，这是量子自旋液体的原型理论例子。

合成的多晶 Herbertsmithite 粉末于 2005 年首次报道，最初的磁化率研究显示低至 $2\mathrm{K}$ 时也没有磁序迹象。在随后的一项研究中，验证了低至 $50\mathrm{mK}$ 的磁序缺失，非弹性中子散射测量（inelastic neutron scattering）揭示了广谱的低能自旋激发，低温比热测量具有幂律比例。这为具有无间隙 $S=1/2$ 自旋子激发的自旋液态提供了令人信服的证据。一系列广泛的附加实验，包括 ${}^{17}\mathrm{O}$ NMR，和动态磁结构因子（dynamic magnetic structure factor）的中子光谱，加强了将 Herbertsmithite 作为无间隙自旋液体材料的鉴定，尽管截至 2010 年确切表征仍不清楚。

Herbertsmithite 的大（毫米尺寸）单晶在 2011 年得到生长和表征。这些能够更精确地测量可能的自旋液体特性。特别是，动量分辨的非弹性中子散射实验（momentum-resolved inelastic neutron scattering experiments）显示了广泛的连续激发。这被解释为无间隙、分形旋转（fractionalized spinons）的证据。后续实验（使用 ${}^{17}\mathrm{O}$ NMR 和高分辨率、低能中子散射）完善了这张图像，并确定实际上存在 $0.07-0.09\mathrm{meV}$ 的小自旋子激发间隙。

一些测量结果暗示了量子临界（quantum critical）行为。这种材料的磁响应在体交流磁化率（bulk ac susceptibility）和低能量动态磁化率（the low energy dynamic susceptibility）中都显示出比例关系，其低温热容量很大程度上取决于磁场。这种标度在某些量子反铁磁体、重费米子金属（heavy-fermion metals）和二维 ${}^3\mathrm{He}$ 中被视为接近量子临界点的标志。

2020 年，使用气体扩散电结晶在室温下合成了 Herbertsmithite 单分散单晶纳米颗粒（$\sim 10\mathrm{nm}$），表明它们的自旋液体性质在如此小的尺寸下仍然存在。

15.5.3 Kitaev spin liquids

图 YbRh2Si2 在不同磁场下的电子比热 C/T 的 T 依赖性，如图例所示。显示了 B=8 Tesla 时的 (C/T)max 和 Tmax 值。最大值 (C/T)max 随着磁场 B 的增加而降低，而 Tmax 向更高的 T 移动，在 B=18 Tesla 时达到 14 K。观察到 C/T~χ~M*，可以得出结论，在后续图片所示的 ZnCu3(OH)6Cl2 中的 SCQSL 表现出与 YbRh2Si2 中的重费米子相似的行为。

2015 年 8 月，在二维材料中观察到量子自旋液体的另一个证据。橡树岭国家实验室的研究人员与剑桥大学的物理学家和德国德累斯顿的马克斯普朗克复杂系统物理研究所合作，测量了这些分数粒子（fractional particles）的第一个特征，称为 Majorana fermions，在具有类似于石墨烯的结构的二维材料中。他们的实验结果成功地与量子自旋液体的主要理论模型之一相匹配，称为 Kitaev honeycomb model。

15.5.4 强相关量子自旋液体

图 ZnCu3(OH)6Cl2 在不同磁场下的磁化率 χ 的 T 依赖性。显示了 B=7 特斯拉时的 χmax 和 Tmax 值。 B=0 处的 T 依赖性 T(-2/3) 由实线描绘。最大 χmax(T) 随着磁场 B 的增大而减小，而 Tmax(B) 向更高的 T 移动，在 B=14 特斯拉时达到 15 K。观察到 χ~C/T~M*，可以得出结论，前续所示的 YbRh2Si2 的比热表现出与 χ 相似的行为。因此，ZnCu3(OH)6Cl2 中的 SCQSL 在 YbRh2Si2 中表现为重费米子。

强相关量子自旋液体（strongly correlated quantum spin liquid，SCQSL）是一种可能的量子自旋液体的具体实现，它代表一种新型强相关电绝缘体（strongly correlated electrical insulator，SCI），除了一个例外，它具有重费米子金属的特性：它抵抗电荷的流动。在低温 $T$ 下，这种类型的绝缘体的比热与 $T^n$ 成正比，其中 $n$ 小于或等于 $1$ 而不是 $n=3$，因为它应该是在传统绝缘体的情况下，热容量与 $T^3$ 成正比。当磁场 $B$ 施加到 SCI 时，比热很大程度上取决于 $B$，这与传统绝缘体相反。 SCI 的候选人有几个；其中最有前途的是Herbertsmithite，一种化学结构为 $\mathrm{ZnC}{\mathrm{u}}_3(\mathrm{OH}{)}_6\mathrm{C}{\mathrm{l}}_2$ 的矿物。

15.5.5 Kagome type

$\mathrm{C}{\mathrm{a}}_{10}\mathrm{C}{\mathrm{r}}_7{\mathrm{O}}_{28}$ 是一种阻挫的 Kagome bilayer magnet，即使在 $1\mathrm{K}$ 以下也不会产生长程有序，并且具有无间隙激发的扩散光谱。

15.6 Toric code type

2021 年 12 月，首次报道了对 toric code type 的量子自旋液体的直接测量，由两个团队实现：一个在量子处理器上探索基态和任意子激发，另一个在量子模拟器上用光镊固定的红宝石晶格上实现原子的理论蓝图。

15.7 具体性质：拓扑费米子凝聚量子相变（Topological fermion condensation quantum phase transition）

在重费米子（heavy fermion，HF）金属和二维 Helium-3 上收集的实验事实表明，准粒子有效质量 $M\ast$ 非常大，甚至发散。拓扑费米子凝聚量子相变（fermion condensation quantum phase transition，FCQPT）保留准粒子，并在费米能级形成平坦的能带。 FCQPT的出现与有效质量 $M\ast$ 的无限增长直接相关。在 FCQPT 附近，$M\ast$ 开始取决于温度 $T$、数密度 $x$、磁场 $B$ 和其他外部参数，例如压力 $P$ 等。与基于有效质量近似恒定假设的朗道范式相反，在 FCQPT 理论新准粒子的有效质量强烈依赖于 $T$、$x$、$B$ 等。因此，为了与众多实验事实一致/解释，必须引入基于 FCQPT 的扩展准粒子范式。这里的要点是，定义明确的准粒子决定了强相关费米系统的热力学、弛豫、标度和传输特性，而 $M\ast$ 成为 $T$、$x$、$B$、$P$ 等的函数。收集的数据非常不同相关的费米系统展示了普遍的标度行为；换句话说，具有强相关费米子的不同材料出人意料地变得均匀，从而形成了一种新的物质状态，由 HF 金属、准晶体、量子自旋液体、二维 Helium-3 和表现出高温超导性的化合物组成。

15.8 应用

支持量子自旋液态的材料可能在数据存储和存储器中具有应用。特别是，可以通过自旋液体状态实现拓扑量子计算（topological quantum computation）。量子自旋液体的发展也可能有助于理解高温超导性。

16. 价键玻璃态（valence bond glass，VBG）

当年，大神安德森提出量子自旋液体 (quantum spin liquid) 的 RVB（resonating valence bond）模型时，大概没有想到 RVB、自旋液体等概念对量子凝聚态是那么重要，大概没想到它会在三四十年后成为量子磁性 (或者干脆叫量子磁学，quantum magnetism) 的核心概念和骨架元素之一。这个领域，已经诞生的非常规超导、自旋电子学、自旋玻璃、Kitaev 物理、现代多铁性和量子纠缠与信息等前沿分支方向，多少与这个概念有所关联。

所谓量子磁性，关键词是“量子”。对固体而言，量子及其“涨落”，可以分别归结到微观局域实空间和宏观广域动量空间，如下图所示的冷原子实验研究量子磁性。固体物理和量子材料更关注后者，其中量子涨落的能量尺度可以很小而须到极低温，也可以通过形成宏观量子态而展现较大能量尺度、存活于较高温度，从而为我们所用（当然，不大可能远高于室温）。这是能量尺度上的约束。

图 量子磁性研究的一个例子：利用晶格中的原子来研究电子自旋行为。 In a magnetic material, electrons interact with each other. In the quantum simulator of ETH researchers, atoms (red and blue) take the role of electrons. They are embedded in a «crystal» (grey) made of interfering laser beams. https://www.ethlife.ethz.ch/archive_articles/130524_quantenmagnetismus_at/index_EN.html

量子磁性当然还含有“磁性”。往大里说，凝聚态物理中与磁性相关的“铁性物理（磁学、铁电 / 多铁、铁弹）”各个分支中，磁学最早获得量子力学青睐，以海森堡的量子磁性理论为代表。但磁学的大规模应用，实际上并未牵涉太多量子物理，因为经典磁学在大多数情况下就够用了。铁电压电多铁性物理更是如此，将量子物理拥入怀抱，只是最近的事情。而铁弹物理，应该说至今也没有其独有的量子理论。

“量子”和“磁性”这样分离的局面，对“量子材料”而言显然不合适，量子材料人显然也不能容忍此状。在量子磁性发展壮大的今天，局面有了一些变化。这里面临的最大困难，用较为粗鲁、也还科普的话来挑明，就是如何能发展出一些物理框架，使得能量尺度很小的量子涨落，能够在能量尺度较大的磁性体系中凸显出来。

稍微了解一些量子材料的物理人，都马上能意识到：这样的困难，由于如下两个要素的认识，正在渐渐得到缓解：

（1）电子关联：电子关联，在很大程度上压制了电子输运进程，即压制了动能和动量，给了电子自旋 / 轨道物理以露脸的机会。由于电子关联导致的显著局域化 (例如莫特绝缘化)，能量高的电荷输运被冻结，能量低的自旋动力学过程成为主角。这是第一步，万物开始归于沉寂，一切开始走向安静，即标题中“无”之一。

（2）自旋阻挫：即便自旋动力学成为主角，自旋交换依然具有较高能量尺度，如 $\sim 100\mathrm{meV}$ 及以上，依然可以兴风作浪，结果就是体系磁基态纷纷迈向反铁磁序。量子材料人的第二招，便是寻找高度自旋阻挫的磁体。在那里，晶体结构的高度对称，磁性离子占位基本有序，两者使得自旋交换能捉对抵消、或者说交换作用成双成对两两相消。这些细致而惟妙惟肖的抵消，便将磁有序之路堵死，即标题中“无”之二。

此时，整个体系能剩下的物理，其能量尺度就很小了，基本上就是量子涨落的宏观表现尺度！由此，量子磁性的各种物理效应登堂入室，开始扮演自己的角色，形成若干新的量子序或量子态，即标题之所有“有”。这些角色中，有一些令人难忘、有一些惟妙惟肖。Ising 本是外行，只能列举其中十一，而且还很不准确：

（1）关注 ${\mathrm{J}}_{\mathrm{eff}}=1/2$ 体系。开展量子磁性研究，总要有承载显著量子磁性的材料池，池中鱼龙越多越好。首选的，当然是那些交换耦合较弱（$J=1/2$）的体系，如 Cu 基化合物。这些体系，$J$ 小，整体能量尺度小，给量子效应以展示机会。随后，若干具有较高晶格对称性的过渡金属离子体系，因为能级填充、晶体场劈裂、自旋 - 轨道耦合等联动介入，体系展现出等效交换耦合很小的情形，即 ${\mathrm{J}}_{\mathrm{eff}}=1/2$ 属性。最近若干年，${\mathrm{J}}_{\mathrm{eff}}=1/2$ 体系正在成为量子磁性的一类重要目标。

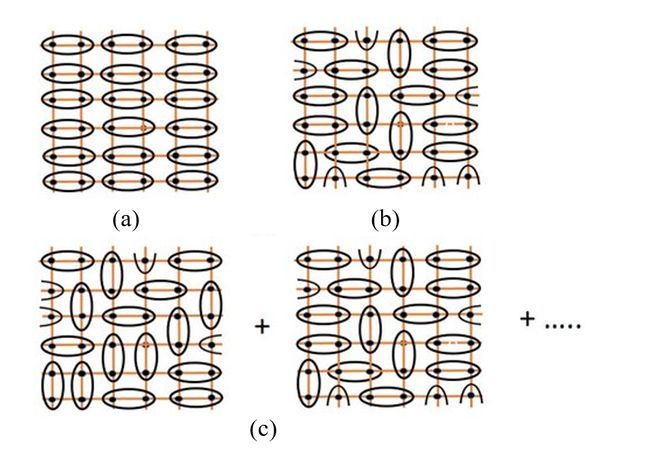
（2）关注 resonating valence bond（RVB）。这个模型最开始由 Pauling 提出，后来用于描述金属体系电子结构。应该是在 1987 年，安德森借鉴之，去描述高温超导中反铁磁基态向超导态转变的进程：晶格中相邻自旋，两两通过价键结合成反向排列的 dimers。所有 dimers 同步叠加，形成所谓的共振价键态 RVB 态，如下图 © 所示。此态没有长程序，但却具有自旋单态（singlet）的长程纠缠。对此，如何适当地掺杂载流子（holes）到点阵中，以破坏其中一些 dimers、形成载流子，就成为走向超导电性的征程！这些可迁移的载流子，也两两成对，被认为就是电子库珀对。整个点阵，也就成为库珀对海。海的凝聚，对应一个量子相变，结果就是超导态（Ising 所言过于粗略，对错请不以为意）。

（3）关注 quantum spin liquid（QSL）。这样的 RVB 体系，应该是所谓量子自旋液体（QSL）雏形。也因此，量子材料人开挂起来，到处寻找能承载 QSL 态的体系。包括《npj QM》在内的很多期刊，开始陆续收到研究报告，宣称了一波一波的 QSL，其中风霜冷暖就不在此展现了。QSL，可以被粗暴地认为是一个经典磁学意义上什么都没有的“无”的量子态。Ising 以为，物理学上，证明“无”比证明“有”要困难得多。运用到 QSL 就是如此：在当下凝聚态物理学中，鲜有合适的物理量去表征一个 QSL 态，因为它几乎什么都“没有”，除了这个 proposed 的 RVB。而 RVB 怎么测量？

（4）关注低能激发。既然不能确定“无”，那看看低能激发态中是否存在“有”，总可以的吧？阅读文献报道的实验，除了一系列展示“无”的测量数据外，最有力的就是低能激发态特征，包括自旋波激发谱的细致解读 (这一问题似乎正在变成一个独立的方向)。稍有遗憾的是，不少实验揭示：对应这种、或者那种激发态的基态，似乎不是唯一的！例如，结构无序、自旋玻璃等，都有可能导致类似的激发特征。于此，从因果逻辑上讲，拿激发态去印证基态，也许就有了些许不确定性。正是这种一个结果可能有多个原因的现状，反过来促使量子材料人问：除了自旋玻璃、RVB、自旋液体等物态外，量子磁性还“有”、“没有”更多的类自旋液体态？如果有，是什么？

（5）关注 Kitaev 物理。Ising 感觉 (也许是胡乱猜测)，Kitaev 模型是能够部分回答 QSL 中“无中生有”这个问题的难得的好物理。或者说，因为有了这个了不起的 Kitaev 模型，我们懂得了去寻找更多类自旋液体基态的重要性。更进一步，因为这个模型有严格解，且展示了一些物理标记，量子磁性物理便有了一丝“唯我独尊”的味道：凝聚态物理有几个模型是可以严格求解的呢？！所以，我们看到，Kitaev 教授获奖无数。

图 想象中的 (a) VBC (valence bond crystal (2D))、(b) VBG (valence bond glass (2D) ? )。在 (c) 中，一系列“无限”的、类似于 (b) 中的无序 valence bond structures 叠加起来，即形成 RVB (resonating valence bond) 态。 图片取自 https://www.researchgate.net/publication/334049314_Possible_glass-like_random_singlet_magnetic_state_in_1T-TaS2

在量子磁性名目下，在“电子关联”和“自旋阻挫”前提下，还有更多的基态正在被预言。其中受关注最多的两类体系：一是六角晶格类别，如三角、蜂巢 honeycomb、kagome 体系等（考虑面内 2D 对称性）；一是过渡金属层状钙钛矿体系，特别是 4d / 5d 双磁性离子参与的、层状钙钛矿 double perovskite 氧化物（考虑三维 3D 对称性）。对前者，面内极高的对称性，使得面内长程磁序成为稀有、面外磁有序也不多见。对于后者，大部分晶格是 fcc 等高对称性，两类磁性离子有序占据晶格。此时如果不发生晶格对称破缺，这样的体系自旋阻挫一定最完美、一定会缺失长程磁有序。

正因为如此，过去一些年，很多量子材料人试图从中寻找安德森开出的“灵丹妙药”： QSL 及其同类。当然，因为本征难度，真正获得广泛认可的 QSL 并不多，倒是原本为了追逐 QSL 的理论工作预言了阻挫磁性下的诸多新量子态（大多具有反铁磁背景），例如：多偶极序（multipolar order）、价键晶体态（valence bond crystal，VBC）、价键玻璃态（valence bond glass，VBG）等。不那么确切的、想象中的例子于上图所示。

图 具有 4d1 面心立方结构的双钙钛矿 Ba2Lu(Y)MoO6 氧化物的量子磁性相图： noncollinear (coplanar) 铁磁 (F) 相和反铁磁 (AF) 相、非磁性的 disordered dimer phase (？VBG state). Judit Romhányi et al, Phys. Rev. Lett. 118, 217202 (2017), https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.217202 https://www.physics.uci.edu/~romhanyigroup/research.html

过去若干年，试图从双离子过渡金属层状钙钛矿中寻找 QSL 及相关量子态的努力很多，最受关注的体系之一是 $\mathrm{Re}{\mathrm{B}}^{\prime }B"{\mathrm{O}}_6$，其中 $\mathrm{Re}$ 是碱土金属或稀土离子、${\mathrm{B}}^{\prime }/B"$ 是过渡金属离子。最近，来自英国谢菲尔德大学 University of Sheffield的 E. J. Cussen 教授课题组 (https://www.sheffield.ac.uk/materials/people/academic-staff/eddie-cussen)，联合伯明翰大学、卢瑟福同步辐射实验室、伦敦学院大学 University College London 和剑桥大学的合作者一起，致力于在 $\mathrm{Re}{\mathrm{B}}^{\prime }B"{\mathrm{O}}_6$ 氧化物中寻找新的、强阻挫的量子磁性。他们运用常规低温强场下的磁性测量、μSR 表征温度低到 $60\mathrm{mK}$)、高能量分辨的非弹性中子衍射等，以详实的实验数据和精细解谱进程，确认 $\mathrm{B}{\mathrm{a}}_2\mathrm{LuMo}{\mathrm{O}}_6$ 这一 $4{\mathrm{d}}^1$ 面心立方体系，具有 ${\mathrm{J}}_{\mathrm{eff}}=1/2$ 量子磁性和一种新的 VBG 量子态。主要结果发表于最近的《npj QM》中。

其实，价键玻璃态（valence bond glass, VBG）本身的理论预言，在十几年之前就由理论物理人完成了。来自法国的两位物理人 M. Tarzia 和 G. Biroli，在 2008 年预言了 VBG 这一新的量子磁性玻璃态（The valence bond glass phase, EPL 82, 67008 (2008)）。后来，来自德国斯图加特固体物理研究所的 J. Romhányi 博士他们，与凝聚态名家 Leon Balents 合作，也对 $\mathrm{B}{\mathrm{a}}_2\mathrm{Lu}(\mathrm{Y})\mathrm{Mo}{\mathrm{O}}_6$ 中这一非同寻常的 VBG 态进行了理论构建和相图预测，如上图所示。这些理论工作和 Cussen 课题组的实验工作，揭示出 VBG 态呈现自旋 dimers 的非晶结构，对电子和自旋输运均无能隙，但存在与 QSL 类似的自旋单态 (singlet)。而且，在自旋单态和自旋三重态之间还存在赝能隙 (single - triplet gap, $\sim 28\mathrm{meV}$)，展示出独特的长程价键关联。这一量子态，有一些基于 dimers 集合低能激发的特征，可以用 NMR 和磁弹探测等技术进行表征，虽然结果未必是唯一的。Cussen 教授他们的结果与文献中一系列相关体系的量子磁性态结果整理于下图中。

图 表格展示一系列面心立方结构的双层钙钛矿 ReB'B"O6 氧化物的量子磁性基态。

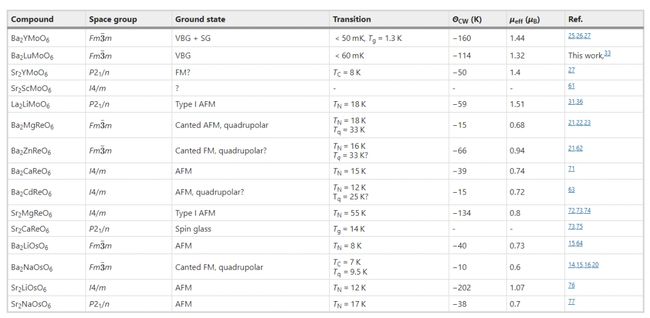
量子材料领域之外的读者可能会疑惑：这样的工作，无非就是在“量子磁性”的名号下确认了一个“新”的量子态，如此而已，谈不上有多大“原创、新颖和 impacting”吧？其实，我们应意识到，对量子磁性态基本性质和激发态开展深入研究，于量子材料领域和面向未来的量子信息领域，都有参考价值。事实上，回看高温超导相图，超导人可是花费了巨大努力，去关注超导穹顶周围的那些反铁磁 AFM、赝能隙 PG、电荷密度波 CDW、自旋密度波 SDW、奇异金属 SM、量子临界点 QCP、费米液体 FL 等量子态及其相互转变。个种缘由，无非一是为促进对超导物理的理解，二是为发现新的量子物理，即“无中生有”。这里关注 QSL 周围的其它量子磁性，给我们类似的感觉。物理人，要立足于重要的物理应用出口，要能洞察研究工作的物理意义与潜在价值。在此基础上，实际去做的，应该是受物理思维自发引导的研究：事情本身的 instant 意义并不重要，或者说我们其实还不知道它是否重要。对这里的（valence bond glass，VBG），大约也是如此！

Valence bond glass state in the 4d1 fcc antiferromagnet Ba2LuMoO6

O. H. J. Mustonen, H. M. Mutch, H. C. Walker, P. J. Baker, F. C. Coomer, R. S. Perry, C. Pughe, G. B. G. Stenning, C. Liu, S. E. Dutton & E. J. Cussen

npj Quantum Materials volume 7, Article number: 74 (2022)

https://www.nature.com/articles/s41535-022-00480-4

---

• 参考文献

wiki: Geometrical frustration

wiki: Quantum spin liquid

Savary, L.; Balents, L. (2017). “Quantum spin liquids: a review”. Reports on Progress in Physics. 80 (1): 016502. arXiv:1601.03742. Bibcode:2017RPPh…80a6502S. doi:10.1088/0034-4885/80/1/016502. PMID 27823986. S2CID 22285828.

wiki: Resonating valence bond theory

wiki: Spinon

Y. Jompol; et al. (2009). “Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid”. Science. 325 (5940): 597–601. arXiv:1002.2782. Bibcode:2009Sci…325…597J. doi:10.1126/science.1171769. PMID 19644117. S2CID 206193.

Schlappa, J; Wohlfeld, K; Zhou, K. J; Mourigal, M; Haverkort, M. W; Strocov, V. N; Hozoi, L; Monney, C; Nishimoto, S; Singh, S; Revcolevschi, A; Caux, J. S; Patthey, L; Rønnow, H. M; Van Den Brink, J; Schmitt, T (18 April 2012). “Spin–orbital separation in the quasi-one-dimensional Mott insulator Sr2CuO3”. Nature. 485 (7396): 82–5. arXiv:1205.1954. Bibcode:2012Natur.485…82S. doi:10.1038/nature10974. PMID 22522933. S2CID 205228324.
“Not-quite-so elementary, my dear electron”. 18 April 2012.

Ising (网名). “无中生有”个价键玻璃态.2022.10.07.

wiki: Spin ice