《数据挖掘与大数据分析》课堂学习笔记-10 第五章 聚类
聚类分析是常见的数据挖掘手段
本课来进行一个简单的学习
参考课程ppt及
聚类分析：如何用最通俗的话解释清楚？
深入浅出聚类算法
然后进行了一个简单的总结+个人理解&延伸
文章目录
- 1.引入
- 2.什么是聚类分析？
-
- 有监督学习：分类问题
- 无监督学习：聚类算法
- 3.簇
- 4.聚类的方法
-
- 1.K-Means聚类算法
-
- 【1】确定分组数
- 【2】随机选择K个值作为数据中心
- 【3】计算其他数值与数据中心的距离
- 【4】重新选择新的数据中心
- 【5】再次计算其他数据与新数据中心的距离
- 【6】再次重新选择数据中心
- 【7】再次计算其他数据与新数据中心的距离
- 方法小结
- Sklearn中的K-均值
1.引入
聚类问题是机器学习中无监督学习的典型代表，应用于数据分析、模式识别等多个实际问题。
接下来 举一个实际业务分析场景中的例子：
某零售公司在市面上主要有30款产品，这些产品的类别、销售量和销售额的差异很大，于是该公司的业务分析师想按照一定的标准，将30个产品划分为A、B、C三个等级，以便公司进行产品战略规划，那么他应该怎么做呢？
这个问题可以套用波士顿矩阵
以销售量、销售额为横纵坐标轴，然后计算中心轴 将每个产品落入波士顿矩阵中，就能得到大体的产品分类情况
此实际应用的关键为：应该使用什么标准去衡量和判断中心轴的划分！
直接拉取数据的平均值作为中心轴这种分类方法在实际中可能会造成数据的误判！
因为类别不同，数据之间的差异可能会呈现出族群的现象，这时有些数据可能会混入其他类别之中！
比如，我们可以举个很极限的例子，有A、B、C三个产品的销售量分别为100、50、1
很显然A、B产品为一类，C产品为一类；
但是如果按照平均值151/3=50.03，划分之后A为一类，B与C划分到了一类。
所以说 为了避免“因为中心轴的不合适选取而导致分类失败”，我们来介绍聚类这个分类分析方法
2.什么是聚类分析？
聚类原本上是统计学上的概念，现在属于机器学习中非监督学习的范畴，大多被应用在数据挖掘、数据分析的领域，简单来说 聚类可以用一个词概括
物以类聚
有监督学习：分类问题
在机器学习中，分类问题是最常见的一类问题，目标是确定一个物体所属的类别。
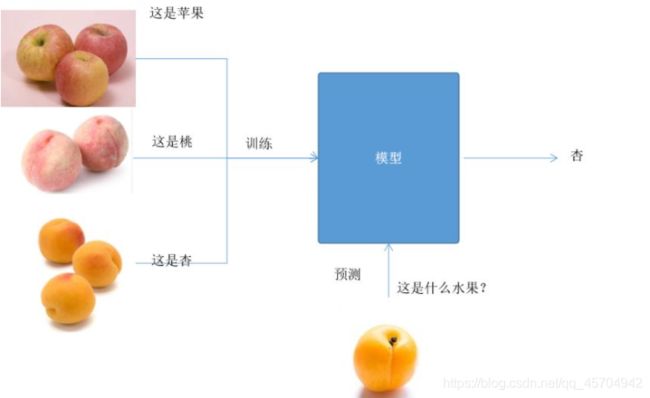
比如说：判定一个水果是苹果、杏，还是桃
判断一个生物是人还是狗还是鱼…
解决这些问题就是先给一些各种类型的水果、生物让算法进行学习，然后根据学习得到的经验对类型进行判定。
这种做法称为有监督学习，有训练、学习&进行预测的过程~
训练、学习阶段：用大量的样本让模型进行学习，从而得到一个判定水果类型的模型。
预测阶段：给一个样本，就可以用模型预测出类别了！
无监督学习：聚类算法
虽说聚类算法的目的也是确定一个物体的类别，但是！聚类和分类可是有很大不同的！
在聚类算法的应用中，我们不会给事先定义好的类别，
这个就是无监督学习
聚类算法必须
- 自己想办法把一批样本分开，分成多个类
- 保证每一个类中的样本之间时相似的
- 不同类样本之间是不同的
聚类算法中，类型被称为“簇”（cluster）。
举个栗子，我们要把这一堆水果进行分类，但是事先没有告诉有哪些水果、且没有一个训练好的模型。
聚类算法要自动将这堆水果进行归类！
聚类算法没有训练过程，这个是和分类算法最本质的区别~
聚类算法要根据自己定义的规则，将类似的样本划分在一起，不相似的样本分成不同的类。
我们是不知道聚类具体的划分标准的！要靠算法进行判断数据之间的相似性，把相似的数据放在一起
聚类最关键的工作是：探索和挖掘数据中的潜在差异和联系。
聚类的结论出来之前 我们是完全不知道每一类有什么特点的 一定要根据聚类的结果通过人的经验来分析，看看聚成的这一类大概有什么特点。
3.簇
聚类学习将数据集中的样本分成若干个互不相交的子集（称为簇cluster)
为了将数据集正确聚类，我们要保持簇内差异尽可能小、簇间差异尽可能大
4.聚类的方法
聚类算法有很多种
- 基于层次的聚类方法 CURE算法
- 基于划分的聚类方法 k均值算法
- 基于网格的聚类方法 STING算法
- 基于密度的聚类方法 DBSCAN算法
- 基于神经网络的聚类方法 SOM算法
- 基于图的聚类方法 Normalized cut
- …
1.K-Means聚类算法
此处学习了
聚类分析：如何用最通俗的话解释清楚？
&
【机器学习】非监督学习初探—聚类
另外 可以通过这个网站 自己设置参数 来感受一下聚类算法的效果~
网站中
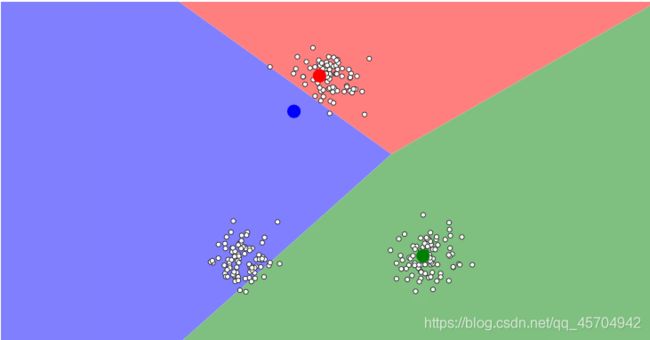
选择 randomly，Guassian Mixture，然后添加3个中心点，
经过多次反复聚类，最终确定中心点的位置
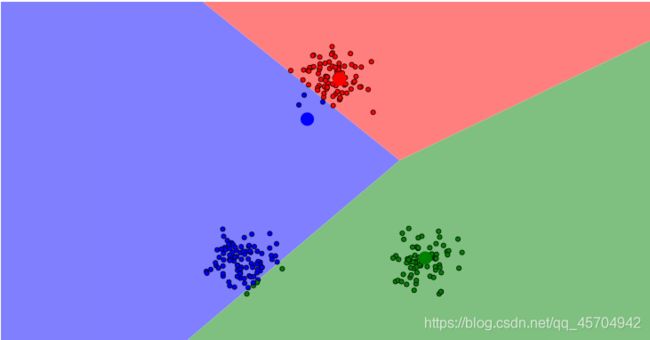
最终通过不断迭代 分组不再变化——
【1】确定分组数
K-Means算法中的“K”就是分组数
我们希望通过聚类后得到“K”个组数
给出例1——下面有8个数据 想分他个两类 那么K=2
例二
选择三个点
【2】随机选择K个值作为数据中心
这个数据中心的选择是完全随机的 也就是说怎么选择都是无所谓的 K=2—以A B两个为数据中心
下面来做个散点图
例二
数据集是随机分布的
对三个数据中心进行选择
【3】计算其他数值与数据中心的距离
如何判断数据中心周围的数据是否与数据中心相似呢？
引入欧式距离的概念
上面的例子中 是二维数据——公式直接变成勾股定理~
我们算出来其余六个点 距离 A B的距离 谁离得更近 谁与数据中心就是同一类
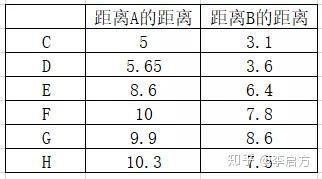
可以看到C-H第一次分组距离B的距离都比A更近
进行分组
- 第一组 A
- 第二组 B C D E F G H
例二
做一个分组——离每个数据中心较近的点被涂上相应的颜色~
【4】重新选择新的数据中心
得到了第一次分组的结果 再重复前两个步骤 重新选择每一组数据的数据中心
- 第一组 A（也只有他一个了！）
- 第二组 取7个数值的平均值 作为新的数据中心 命名为P 计算平均坐标 ——(5.14,5.14)
例二
这里数据还没有更新 只是变更了数据中心（可以看到蓝色的下去了）
【5】再次计算其他数据与新数据中心的距离
使用勾股定理（欧氏距离在二维的表现）计算其他数据与A P的欧氏距离
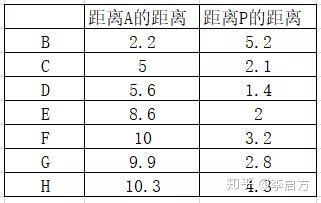
终于有离A要近一些的了~
- 第一组：A、B
- 第二组：C、D、E、F、G、H
例二
更新分组完成
【6】再次重新选择数据中心
疯狂迭代 跟之前一样 找到每一组的数据中心
- 第一组有两个值，平均坐标为（0.5 ，1），这是第一个新的数据中心，命名为O
- 第二组有六个值，平均值为（5.8 ， 5.6），这是第二个新的数据中心，命名为Q
【7】再次计算其他数据与新数据中心的距离
- 第一组：A、B
- 第二组：C、D、E、F、G、H
发现貌似没啥变化 第一组和第二组分组不变——
说明计算收敛已经结束了 不需要继续进行分组了
终于 我们的数据按照相似性分成了两组~
例二
分组不再变化——得出结论：
方法小结
上面举了两个例子 一个有数 一个有图
搭配来看效果更佳嗷~
看过两个例子 总结出方法~
重复进行 选择数据中心-计算距离-分组-再次选择数据中心-再次分组-…
直到分组之后所有的数据都不会再变化 也就得到了最终的聚合结果~
Sklearn中的K-均值
到Sklearn库中康一康封装好的聚类代码实现
点击Sklearn.cluster.KMeans来查看
其中比较重要的是这三个高亮的参数
n_clusters=8：
n_clusters指的是聚类默认分成8组。
根据不同情况 设置不同的分组。
分成几组就设置几个基准点嘛 这个不难理解~
max_iter=300：
max_iter指的是“最多进行多少次的调整中心点”。
可以看到我们上面的例子中 个位数数据&两个基准点分两组只调了两次中心点。
n_init=10：
n_init指的是对数据初始化多少次。
为什么要初始化很多次呢？
因为即使是同样的数据，设置同样数量的中心点，依然可能得到不同的结果。这就是K-均值的局限，所以需要初始化很多次，来查看不同的结果