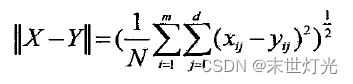高维多元时序数据之间的相似性度量
1. 简介
时间序列作为一种按时间顺序排列的特殊数据,是数据挖掘的重要研究内容,其中包括数据准备、数据选择、数据预处理、数据缩减、数据挖掘目标确定、挖掘算法确定、数据挖掘、模式解释及知识评价9个处理步骤W。数据挖掘方面的方法或算法,按挖掘任务的不同,可W分为W下几个大类:分类知识发现、数据聚类、关联规则发现、数据总结、序列模式发现、依赖关系或依赖模型发现、异常发现和趋势预测等。由于多变量时间序列多噪声、多变量、变量相关性及序列时间维度不等长等问题,増加了对其进行数据挖掘的难度。
单变量时间序列可以看成是向量,其相似度量最常用的两种方法是欧式距离和DTW,将其应用到多元时间序列(可用矩阵存储表达)。
令Q为多元时间序列矩阵,该时间序列共有n个变量,即有n列,每一列维度为m。再令C为另一个多元时间序列,有n个变量,每一列维度为l,m和l不一定相等。
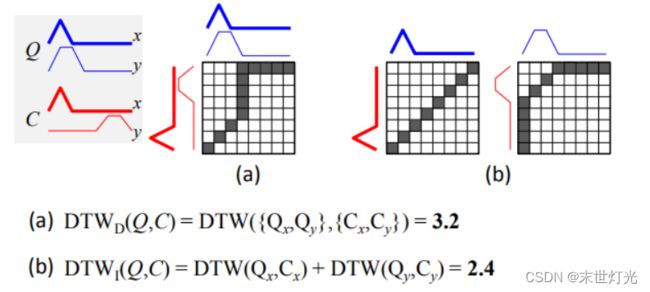
2. 矩阵DTW的两种原始方法
论文地址:https://epubs.siam.org/doi/10.1137/1.9781611974010.33
代码实现:
a:
def matrix_DTW_horizon(X,Y):
m = X.shape[0]
n = Y.shape[0]
matrix_DTW = {}
for i in range(m):
matrix_DTW[(i,-1)] = float('inf')
for i in range(n):
matrix_DTW[(-1,i)] = float('inf')
matrix_DTW[(-1,-1)] = 0
for i in range(m):
for j in range(n):
matrix_DTW[(i,j)] = dist(X[i,:],Y[j,:]) + min(matrix_DTW[(i-1,j)],matrix_DTW[(i,j-1)],matrix_DTW[(i-1,j-1)])
return np.sqrt(matrix_DTW[(m-1,n-1)])
def dist(a,b):
return np.sqrt(sum(np.power(a-b,2)))这里解释一下dist函数:
import numpy as np
a = np.array([1,2])
b = np.array([3,4])
c = np.power(a-b,2)
print(c)
d = sum(c)
print(d)
k = np.sqrt(d)
print(k)def matrix_DTW_vertical(X,Y):
distance = 0
n = X.shape[1]
for i in range(n):
temp = DTW(X[:,i],Y[:,i])
distance = distance + temp # 简单求和?
return distance3. 扩展的欧氏距离
对于两个长度为W、维度为d的多变量时间序列X![]() 、Y
、Y![]() 。它们之间的欧氏距离
。它们之间的欧氏距离
如下:
扩展的欧氏距离定义简单明了,计算也非常快捷。一般用于时间维数大小相同的多变量时间序列。对于时间维数大小不相等的多变量时间序列,若想使巧扩展的欧式距离计算相似性,可采用滑动窗口取最小值的方式。
4. 扩展的Frobenius范数距离
论文:基于Eros的多元时间序列相似度分析 (ceaj.org)
扩展 Frobenius 范数(Eros)的主元分析方法(Principal Component Analysis,PCA)可以检测两个矩阵的相似性,其主要步骤如下,首先,估算两个 MTS元的协方差矩阵,接着计算其特征值和特征向量,最后通过在MTS数据集中获得的特征值来测量相应的每个MTS元的相似性。
在范数概念的基础上,对于一个 mxn 的矩阵 A 的加权F-范数为:
5. PCA相似因子
6. CPCA_SWDTW
通过分别引入共同主成分分析和改进加权动态时间弯曲方法,提出一种考虑多元时间序列变量相关性和形状特性的相似性度量方法CPCA_SWDTW。首先,引入主成分分析方法(Principal Component Analysis,PCA),对具有内部相关性的MTS转换为相互独立的序列。为了将MTS序列转换到同一个维度空间,需要使用共同主成分分析方法(Combined Principal Component Analysis,CPCA)将MTS序列合并后进行主成分分析变换,再分解成相互独立的主成分序列。同时,由于各主成分序列相对于转换后的MTS序列的重要性不同,为了区别各主成分序列的重要性差异,将各维主成分序列的方差贡献率作为各维序列的权重。其次,在降维后的相互独立主成分序列基础上,针对现有动态时间弯曲算法没有考虑序列形态特性的问题,提出了一种基于局部形状特征改进的加权动态时间弯曲相似性度量方法(Shape based Weight Dynamic Time Warping,SWDTW),并用该算法对降维后的独立主成分序列进行相似性度量,从而作为多元时间序列的相似性度量指标。
为了将现有MTS各个变量转换成相互独立的变量,本章首先采用共同主成分分析方法CPCA,将MTS看成矩阵,通过计算各个变量之间的协方差矩阵,将当前变量映射到相互独立的特征空间。其本质上就是将现有的具有相关性的MTS转换成相互独立的MTS。
同时,PCA方法可以用贡献率较大的几个主成分表示原序列,可以对原序列进行降维。同时各个主成分序列由于贡献率不同,具有不同的重要性。因此,在对整个时间序列进行相似性度量时,可以将各个维度的重要性考虑在内,在综合各个维度的相似性度量值时将累积贡献率作为权重值。
在运用CPCA对原MTS进行转换,从m维空间转换为n维空间后,就可以运用改进的加权动态时间弯曲方法SWDTW对转换后的n维空间中的时间序列进行相似性度量。以下给出了基于CPCA变换和SWDTW的MTS相似性度量方法分析框架。
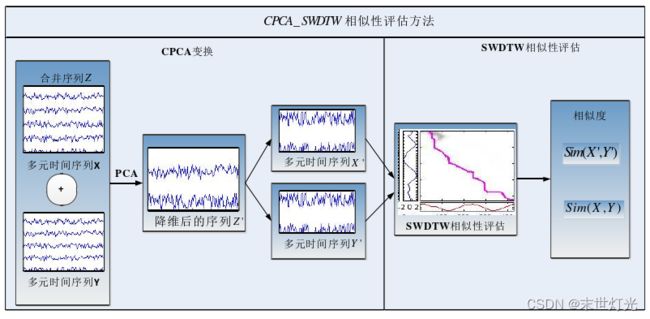 标基于CPCA变换和SWDTW的MTS相似性度量分析框架图
标基于CPCA变换和SWDTW的MTS相似性度量分析框架图
题