深度学习笔记：用卷积神经网络进行MNIST手写数字识别
目录
0. 前言
1. Sequential类 vs 函数式API
1.1 基于Sequential类的方式
1.2 基于函数式API的方式
1.3 神经网络的参数个数以及每层的数据维度变化
2. 编译和训练
2.1 数据加载和预处理
2.2 用原始的(整数值型)标签进行编译和训练
3. 模型评价
3.1 在测试集上的表现
3.2 出错的样本长啥样？
4 用分类编码(Categorical Encoding)型标签
5 Summary
0. 前言
上一篇深度学习笔记：基于Keras库的MNIST手写数字识别
https://blog.csdn.net/chenxy_bwave/article/details/121873968我们用全连接层(Dense layer)实现了一个分类器用于MNIST手写数字识别。但是由于MNIST的数据样本是28x28的图像，所以更适合于用卷积神经网络来实现它的识别任务。本文就来介绍如何构建一个简单的卷积神经网络用于MNIST手写数字识别。
首先把后面代码要用到的库先加载一下。
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import utils
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
1. Sequential类 vs 函数式API
Keras中定义模型有两种方法：一种是使用Sequential类，仅限于以层的线性堆叠的方式构建模型，线性堆叠也是最常用的神经网络结构；另一种是函数式API(functional API),用于由层模块构成有向无环图，以这种方式可以构建任意形式的网络结构。以下我们分别以这两种形式搭建一个用于MNIST识别的简单的卷积神经网络，以对比两种模型构建方式的不同之处。但是，在现在这个简单的例子中，两种形式的模型构建方式没有什么差异。
1.1 基于Sequential类的方式
model_seq = keras.Sequential([
layers.Conv2D(filters=32, kernel_size=3, activation="relu"),
layers.MaxPooling2D(pool_size=2),
layers.Conv2D(filters=64, kernel_size=3, activation="relu"),
layers.MaxPooling2D(pool_size=2),
layers.Conv2D(filters=128, kernel_size=3, activation="relu"),
layers.Flatten(),
layers.Dense(10, activation="softmax")
])
# **Build the model and displaying the model's summary**
model_seq.build(input_shape=(None,28,28,1))
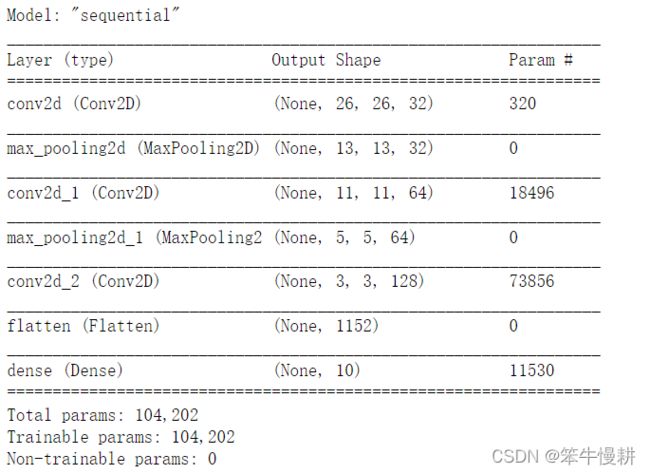
model_seq.summary() 
1.2 基于函数式API的方式
inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.MaxPooling2D(pool_size=2)(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
# **Displaying the model's summary**
model.summary()最后model.summary()打印出来的结果于上一节完全一致。这也说明了两种模型构建方式本质上是一致的。
但是要注意的一点是，Sequential类方式构建时，在调用model.summary()之前需要先调用model.bulild()，传入参数input_shape告诉模型它的输入数据的shape，否则没法计算参数量。当然，也可以它的第一层layers.Conv2D()中通过参数input_shape指定输入数据的shape。
1.3 神经网络的参数个数以及每层的数据维度变化
大家可能会好奇以上model.summary()打印出来的信息是怎么来的，具体来说，就是神经网络的参数的个数，以及层与层之间的数据维度是按什么规律变化的。
To be added.
2. 编译和训练
数据的加载和预处理在上一篇已经做了简单的解释，这里就不再赘述了。
这里我们考虑两种标签向量化的方法。
第一种方法是直接将标签列表转换为整数张量，其实就是用原始的整数型标签，即原来的{0,1,2,...9}标签值；
另一种方法是使用one-hot编码。one-hot编码是分类数据广泛使用的一种格式，也叫分类编码(categorical encoding)。
对应于两种标签表示方式，虽然都是使用交叉熵(crossentropy)损失函数，但是形式上有所不同。整数类型标签对应的损失函数为sparse_categorical_crossentropy；而使用分类编码标签时，对应的损失函数为categorical_crossentropy。
这一章的训练我们仍然使用{整数类型标签, sparse_categorical_crossentropy}，在以函数API方式构建的模型上进行训练.
2.1 数据加载和预处理
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype("float32") / 2552.2 用原始的(整数值型)标签进行编译和训练
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
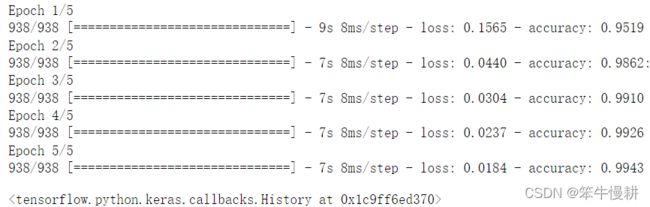
model.fit(train_images, train_labels, epochs=5, batch_size=64)
上一篇基于Dense layer的模型在训练集上的accuracy是略小于98.9%，而这里达到了99.4%! 虽然似乎差异不大，其实是一个非常大的进步，在这么高的accuracy范围取得0.1%的进步都是非常困难的。或者反过来看错误率会更加容易理解一一些，错误率从1.1%下降到0.6%，相对下降了45%!
3. 模型评价
3.1 在测试集上的表现
仍然用evaluate()来评估在测试集上的表现。
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(f"Test accuracy: {test_acc:.3f}")313/313 [==============================] - 1s 3ms/step - loss: 0.0267 - accuracy: 0.9917 Test accuracy: 0.992
同样，相比基于Dense layer的模型的98%有大幅度的提升。但是，如上所示，还是有0.83%的错误率，10000个测试样本有83个判断错误。下面我们来看看这些导致模型错判的样本究竟是长得怎么样，竟然骗过了神经网络的火眼金睛。
3.2 出错的样本长啥样？
首先用predict()计算模型对于每一个输入的输出。注意，
(1) evaluate()其实内部也是调用predict()的，但是它只给出了最终的loss和accuracy。
(2) 针对每个数据样本，输出是一个长度为10的向量，其中每个元素表示对应类别的概率，其中概率最大的即为预测值，概率值可以理解为结果的可信度。参考以下输出例。
predictions = model.predict(test_images)
print(predictions[2])
print(predictions[2].argmax())
test_labels[2][2.9075080e-09 9.9999452e-01 4.3390884e-07 3.4823213e-13 1.6539088e-06 8.4169738e-09 7.5451565e-09 2.9908574e-06 3.3132730e-07 1.9043126e-08] 1
Out[9]: 1
其中第2项为0.999，说明神经网络非常确信这就是一个1.
接下来我们根据预测结果原test_labels的对比把判断错误的数据样本抽取出来。error_index就是所有出错样本在test_images中的序号。
print(predictions.shape)
predicted_labels = predictions.argmax(axis=1)
print(predicted_labels, test_labels)
error_index = (predicted_labels != test_labels)
print(sum(error_index))以下把出错样本的图像，判断值与原标签 ，模型输出中最大的概率值打印出来（总共有83个错误，这里只打印了前10个出来）。
pred_probs = predictions[error_index]
pred_labels = predicted_labels[error_index]
gt_labels = test_labels[error_index]
error_images = test_images[error_index]
print(error_images.shape)
for k in range(0,len(gt_labels),10):
plt.imshow(error_images[k], cmap=plt.cm.binary)
plt.show()
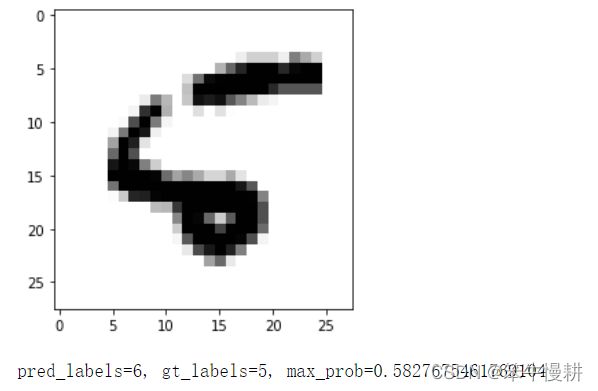
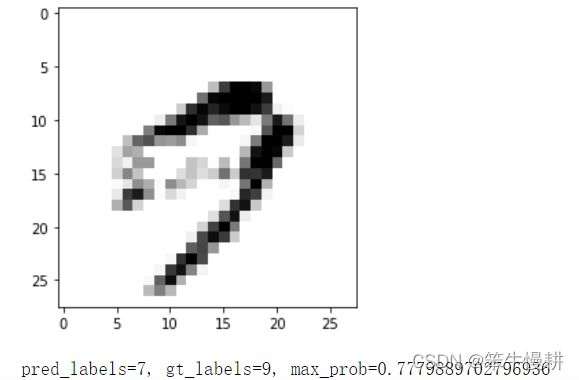
print('pred_labels={0}, gt_labels={1}, max_prob={2}'.format(pred_labels[k], gt_labels[k], np.max(pred_probs[k])))以下为打印结果（仅列几个例子，有兴趣的小伙伴自己运行以上代码观察结果）：
原值为5，本模型判断成6了，站在神经网络的角度来看，确实也有那么一点6的样子^-^。而且概率值只有58%，神经网络也不是觉得特别有把握。
这个判断错误站在人类的角度来说有点离谱，神经网络以83.5%的概率认为这是一个0！
这个有点为难了，9的头上闭环的那一段像素值太浅了，由此导致神经网络看错了？
4 用分类编码(Categorical Encoding)型标签
前面提到还有一种标签表示方式，即分类编码标签，也叫One-hot编码。
在这种编码中，每个标签被转换为一个维数为K的向量，K对应分类数。这个K维向量只有一个元素为1，其余元素为0。在本例中，原始标签已经被指定为0~9的整数，那么对应下标为该标签值的元素值被置为1，其余为0。在一般的情况下，只不过多了一个将标签种类赋予一个[0.K-1]的整数值的步骤，再基于该整数标签值进行one-hot编码。
比如说，原标签为3则转换为[0,0,0,1,0,0,...]，原标签为7则转换为[0,0,0,0,0,0,0,1,0,0,0].
这里我们用{分类编码标签, categorical_crossentropy}，在以Sequential方式构建的模型上进行训练。Keras提供了to_catgorical()函数用于对标签进行格式转换。
from tensorflow.keras.utils import to_categorical
train_labels_cat = to_categorical(train_labels)
test_labels_cat = to_categorical(test_labels)
model_seq.compile(optimizer="rmsprop",
loss="categorical_crossentropy",
metrics=["accuracy"])
model_seq.fit(train_images, train_labels_cat, epochs=5, batch_size=64)毫不意外地，训练结果与上面的训练结果高度吻合（细微的差异可以理解为训练过程的随机打乱顺序所致的随机性效应）
5 Summary
以上我们基于tensorflow.keras库搭建一个简单的卷积神经网络模型用于MNIST数据集（手写体数字）的识别，达到了99.13%的分辨准确度！
在这一篇中，顺便学习了以下几个知识点：
(1) 基于Sequential类和基于函数式API的模型构建方式的对比，
(2) 整数型标签表示方式以及One-Hot编码（分类编码, categorical encoding）标签表示方式
(3) 对出错样本的观察示例
期待后续更加精彩！
上一篇：深度学习笔记：基于Keras库的MNIST手写数字识别