机器学习课程讲义·第四章，支持向量机

本文是中央财经大学机器学习课程系列讲义第四篇，持续更新，不足之处敬请指正！

上期回顾

上期我们一起学习了决策树模型，重点介绍了决策树模型的基本思想、相关的损失函数以及为什么使用这样的损失函数；我们还讨论了如何使用决策树模型来解决回归问题；此外，我们借助决策树模型讲解了机器学习中的一种非常重要的思想：集成学习思想，并由此引出现在目前使用较为广泛的随机森林模型。

本期导读

本章我们将来学习机器学习基础核心算法中最复杂的模型：支持向量机，我们将首先针对线性可分的问题介绍支持向量机的基本思想，并引出硬间隔支持向量机。在讨论硬间隔支持向量机的过程中，我们将重点讲解一种常用的优化算法-拉格朗日乘子法。之后我们进一步放松线性可分的假设，讨论软间隔支持向量机模型。
本章我们还将学习到一种机器学习中十分重要的处理技巧：核技巧，讨论它在支持向量机中的应用。
最后，本章由分类问题到回归问题，讨论支持向量回归机模型。

符号形式

遵循第二章约定的符号形式。

假定$N$个数据集合，记为$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$,其中输入空间$x_i\in R^P$，输出空间$y_i\in R$；输入矩阵记为$X=(x_1,x_2,\cdots ,x_N{)}^T$，输出矩阵记为$Y=(y_1,y_2,\cdots ,y_N{)}^T$，即$X\in R^{N\times P}$，$Y\in R^{N\times 1}$。

引言

第二章我们学习了使用一般线性回归模型处理回归问题，对于分类问题，我们可以将线性回归模型得到的连续值通过映射函数映射到0到1的区间内，即得到逻辑回归模型。逻辑回归模型使用的映射函数是sigmoid函数，除此之外，我们还可以使用简单的符号函数进行映射，即： $$f(x)=\mathrm{sign}({\mathbf{w}}^T\mathbf{x}+b)\text{\hspace{1em}(4-1)}$$这就是感知机模型。关于感知机的历史和更多内容我们将在神经网络的章节中介绍，本章我们只从图形上来认识感知机模型。

如图4-1，感知机模型实际上是找到一个超平面，将线性可分的正负样本分成两部分，超平面的法向量是$w$（之后用$w$代表该超平面），超平面上的点满足${\mathbf{w}}^T\mathbf{x}+b=0$，正样本满足${\mathbf{w}}^T\mathbf{x}+b⩾0$，负样本满足${\mathbf{w}}^T\mathbf{x}+b⩽0$。

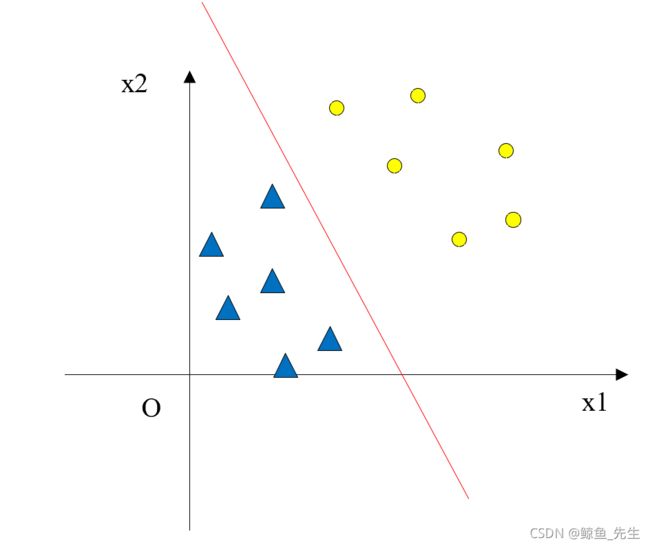
观察超平面${\mathbf{w}}^T\mathbf{x}+b=0$，如果对其稍微进行旋转，只要依然保证正负样本分别在超平面的上方和下方都是可以的，也就是说感知机拥有无穷多个解。那么哪个解（超平面）才是最优的呢？容易想到，最优超平面应该“尽可能”地将正负样本分开，以确保模型的泛化性能最好。

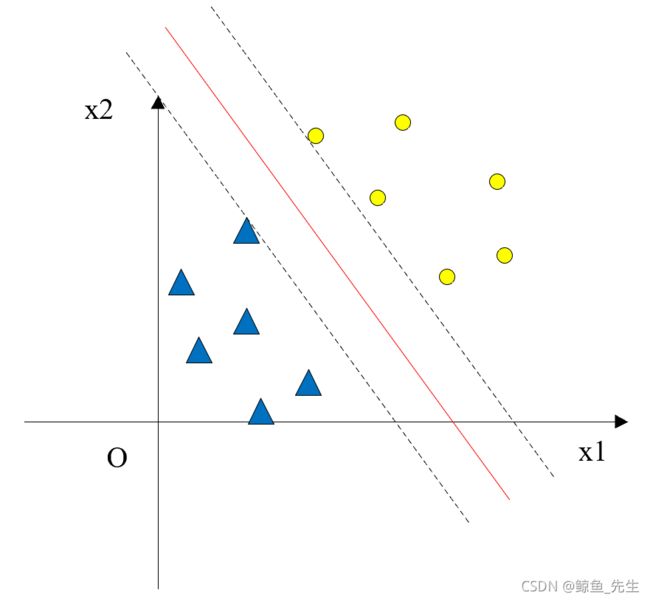
观察图4-2，找到一条超平面，使得其到正类样本最近的距离和到负类样本最近的聚类最大且相等，这样的超平面能够最大程度地将正负样本分开，这个超平面就是最优超平面，此时距离超平面最近的点（包括正类和负类）对超平面的确定有决定性作用，叫做支持向量，这就是支持向量机最初的构想。

支持向量机（Support Vector Machine，SVM）是Cortes和Vapnik于1995年提出的一种基于统计的分类模型，可以说在深度学习流行之前，支持向量机是最有效的一类统计机器学习模型。直至今天，对支持向量机算法的研究和应用依然是相关领域的热点。同时支持向量机也是机器学习经典算法中涉及数理知识最多的模型之一，掌握支持向量机的推导始末，其他机器学习模型的学习就自然不在话下了。

我们首先来总结支持向量机的主要内容。俗话说得好，SVM有三宝：间隔、对偶、核技巧。第一宝即上述对最大间隔的设定，第二宝是为了求解支持向量的优化目标，由于这个优化目标的原问题难以求解，我们可以引入拉格朗日对偶方法进行求解，第三宝“核技巧”一方面实现了输入空间向高维空间的映射，大大提高了模型的泛化性能，另一方面利用核函数的优良性质可以大大简化运算。由易到难，支持向量机分为硬间隔支持向量机、软间隔支持向量机以及核支持向量机，上述模型是分类模型，此外还有解决回归问题的支持向量回归机，接下来我们就逐一来认识她们。

硬间隔支持向量机

模型形式

首先介绍硬间隔支持向量机（hard-margin SVM）。硬间隔支持向量机解决线性可分问题，如引言中所述，最优的超平面应该是距离支持向量（距离超平面最近的点，包括正类的支持向量和负类的支持向量）最远的那个，设某支持向量点为$\mathbf{w}$，根据点到平面的距离公式，此距离可表示为： $$r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert }\text{\hspace{1em}(4-2)}$$不妨设输出空间$y_i\in \{-1,+1\}$，对于线性可分的数据集合，对数据进行完美分类的超平面应该满足以下条件：对于任意$x_i$有 $$\{\begin{array}{ll}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾0,& y_i=+1\\ {\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩽0,& y_i=-1\end{array}\text{\hspace{1em}(4-3)}$$我们可以将公式4-3统一记作：$$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)⩾0\text{\hspace{1em}(4-4)}$$对于${\mathbf{w}}^T\mathbf{x}+b$，对$\mathbf{w}和b$同时乘以一个不为0的数得到的超平面同原超平面一致，因此对$\mathbf{w}$和$b$进行缩放不影响求解。 我们可以适当缩放这两个参数，令距离超平面最近的支持向量点满足${\mathbf{w}}^T\mathbf{x}+b=1$，于是公式4-4变为： $$y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩾1\text{\hspace{1em}(4-5)}$$同时，公式4-2中的距离可以写成： $$r=\frac{1}{\Vert \mathbf{w}\Vert }\text{\hspace{1em}(4-6)}$$于是，支持向量机的模型形式可以表达如下：寻找超平面$\mathbf{w}$，使得所有的样本点均满足$y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩾1$，并且支持向量到该平面的距离$r=\frac{1}{\Vert \mathbf{w}\Vert }$最大。使用数学公式可以表达为： $$\begin{array}{l}{\max }_{\mathbf{w},b}\frac{1}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,N\end{array}\text{\hspace{1em}(4-7)}$$等价于： $$\begin{array}{l}{\min }_{\mathbf{w},b}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,N\end{array}\text{\hspace{1em}(4-8)}$$这是一个带约束的优化问题，优化目标是凸函数（黑塞矩阵正定），约束条件是线性约束（仿射约束），可行域是凸集，是一个典型的带约束凸优化问题，可以直接使用一些二次规划的套件（QP）进行求解。
同时我们注意到，由于$\mathbf{w}$是$p$维的，这是一个变量个数为$p+1$个，约束条件有$N$个的优化问题，当$p$比较大时，问题求解相对困难；更重要的是，很多时候原始的$\mathbf{x}$不能直接求解（如线性不可分等），我们通常需要将其映射到其它空间，该空间维度不确定（有些时候会达到无限大），这样求解就十分不易。为了解决这个问题，我们可以使用拉格朗日乘子法中的对偶方法。

补充：拉格朗日乘子法

一般形式

拉格朗日乘子法（Lagrange Multiplier Method）解决带约束的优化问题。首先从等式约束开始，设待优化的问题的标准形式为： $$\begin{array}{l}{\min }_{\mathbf{x}}f(\mathbf{x})\\ h_i(\mathbf{x})=0,i=1,\cdots ,p\end{array}\text{\hspace{1em}(4-9)}$$即求使$f(\mathbf{x})$最小的$\mathbf{x}$，有$p$个等式约束。如果目标是求最大值，取相反数变换成最小值即可。

勾走拉格朗日函数： $$L(\mathbf{x},\mathbf{\lambda })=f(\mathbf{x})+\sum _{i=1}^p{\mathbf{\lambda }}_i{h}_i(\mathbf{x})\text{\hspace{1em}(4-10)}$$可以去掉等式约束，转化成求拉格朗日函数的最小值，其中$\mathbf{\lambda }$是新引入的自变量，成为拉格朗日乘子。对所有自变量导，可以得到4-11所示方程组： $$\begin{array}{r}{\nabla }_{\mathbf{x}}f(\mathbf{x})+{\sum }_{i=1}^p{\lambda }_i{\nabla }_{\mathbf{x}}{h}_i(\mathbf{x})=0\\ h_i(\mathbf{x})=0\end{array}\text{\hspace{1em}(4-11)}$$求解该方程组即可得到最优解。这就是拉格朗日乘子法的一般形式。

几何意义

我们尝试从几何意义上理解拉格朗日乘子法。如图4-3所示，我们在二维中观察目标函数，画出其等高线（每条闭合线上的目标函数值相同）以及约束条件所在的曲线（如果$x$是二维的，有一个等式约束时可行域为曲线上的点，有两个以上等式约束时，可行域为不同曲线的交点或者没有交点时为空集），那么如果存在最优解，优解一定出现在等高线和约束曲线相切的地方。因为如果最优点在约束曲线和等高线的割点上，一定会存在另外两个割点，一个在原割点下方，其目标函数值比原割点小/大，一个在原割点上方，其目标函数值比原割点大/小，如图中矩形框中所示。（回忆：第二章LASSO回归最优解容易取得稀疏解的几何意义）
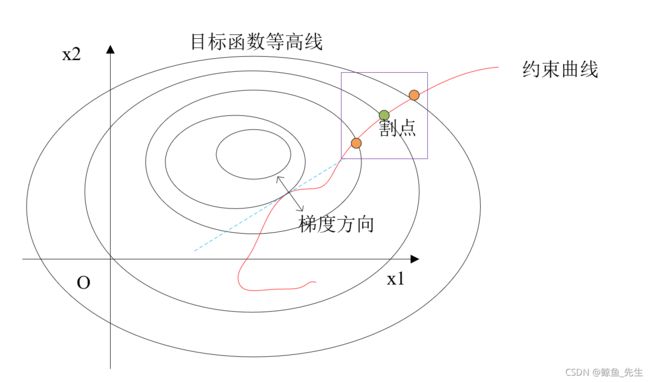明确了最优解在切点处后，容易想到，在切点处，等高线和约束曲线的法向量是共线的，而梯度向量正是曲线的法线。因此，在最优解处，目标函数的梯度和约束曲线的梯度共线（只有一个约束条件）。如果约束条件有多个，如图4-4，容易得出，此时目标函数的梯度是两条约束曲线梯度的线性组合。这就是公式4-11中第一个方程的含义，即： $${\nabla }_{\mathbf{x}}f(\mathbf{x})=-\sum _{i=1}^p{\lambda }_i{\nabla }_{\mathbf{x}}{h}_i(\mathbf{x})\text{\hspace{1em}(4-12)}$$

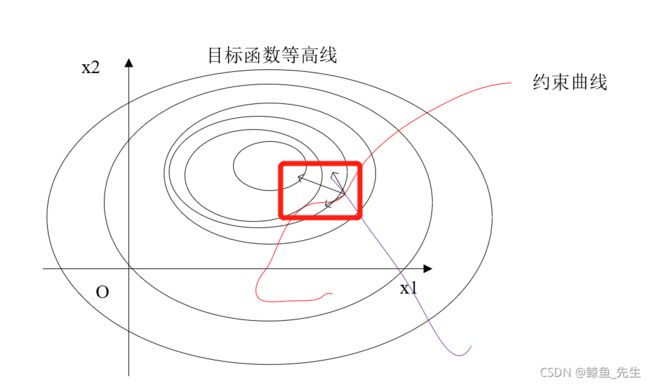
应用举例

回顾第二章讲的线性判别分析（LDA），我们的目标是最大化广义瑞利商，即： $$J=\frac{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}}\text{\hspace{1em}(4-13)}$$同支持向量机中对参数的处理一致，因为$\mathbf{w}$可以缩放，不妨设${\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1$，于是上述目标可以表达成以下最优化问题： $$\begin{array}{l}{\min }_{\mathbf{w}}-{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}\\ \text{ s.t. }{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}-1=0\end{array}\text{\hspace{1em}(4-14)}$$使用拉格朗日乘子法，有拉格朗日函数$L(\mathbf{w},\mathbf{\lambda })={\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_B\mathbf{w}+\lambda \left({\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_W\mathbf{w}-1\right)$，对其求梯度令梯度为0，容易得到：$$\mathbf{w}=\frac{1}{\lambda }{\mathbf{S}}_W^{-1}{\mathbf{S}}_B\mathbf{w}\text{\hspace{1em}(4-15)}$$这与之前我们得到的结论：$w\propto S_w^{-1}{S}_{b}w=S_w^{-1}\left(\overline{x_{c1}}-\overline{x_{c2}}\right){\left(\overline{x_{c1}}-\overline{x_{c2}}\right)}^{T}w\propto S_w^{-1}\left(\overline{x_{c1}}-\overline{x_{c2}}\right)$一致。

进一步分析，公式4-15可以有：${\mathbf{S}}_W^{-1}{\mathbf{S}}_B\mathbf{w}=\lambda \mathbf{w}$，即$\lambda$是${\mathbf{S}}_W^{-1}{\mathbf{S}}_B$的特征值，$\mathbf{w}$是对应的特征向量。进而可以对广义瑞利商写成如下形式： $$\frac{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_B\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_W\mathbf{w}}=\frac{{\mathbf{w}}^{\mathrm{T}}\left(\lambda {\mathbf{S}}_W\mathbf{w}\right)}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_W\mathbf{w}}=\lambda \text{\hspace{1em}(4-16)}$$也就是最优目标值实际上是矩阵${\mathbf{S}}_W^{-1}{\mathbf{S}}_B$的最大特征值，对应的最优解是最大特征值对应的特征向量。

课后练习题

利用拉格朗日乘子法证明周长一定时，等边三角形的面积最大。
提示：优化目标为求三角形面积的海伦公式。

拉格朗日对偶（弱对偶和强对偶）

弱对偶问题

上述讨论的拉格朗日乘子法的约束条件为等式约束，那对于不等式约束我们应该如何求解呢？

考虑以下优化问题： $$\begin{array}{l}{\min }_{\mathbf{x}}f(\mathbf{x})\\ g_i(\mathbf{x})⩽0i=1,\cdots ,m\\ h_i(\mathbf{x})=0i=1,\cdots ,p\end{array}\text{\hspace{1em}(4-17)}$$我们写出它的拉格朗日函数，如下： $$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })=f(\mathbf{x})+\sum _{i=1}^m{\lambda }_i{g}_i(\mathbf{x})+\sum _{i=1}^p{\nu }_i{h}_i(\mathbf{x})\text{\hspace{1em}(4-18)}$$称为广义拉格朗日函数，其中${\lambda }_i⩾0$。相应的优化问题可以写为： $$\underset{\mathbf{x}}{\min }\underset{\mathbf{\lambda },\mathbf{\nu },{\lambda }_i⩾0}{\max }L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })\text{\hspace{1em}(4-19)}$$也就是说首先固定$\mathbf{x}$，找到使得$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$最大的$\lambda ,\mathbf{\nu }$，然后求使得$L(\mathbf{x},{\mathbf{\lambda }}_{\ast },{\mathbf{\nu }}_{\ast })$最小的$\mathbf{x}$。

我们来简单证明一下为什么优化4-19和优化4-17会得到相同的解。

证明如下，分两种情况讨论：

1. 如果$\mathbf{x}$是可行解，也就是满足公式4-17中的约束条件，我们有$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })=f(\mathbf{x})+{\sum }_{i=1}^m{\lambda }_i{g}_i(\mathbf{x})$，因为有$h_i(\mathbf{x})=0$，第三项为0；同时我们要求${\lambda }_i⩾0$，并且$g_i(\mathbf{x})⩽0$，第二项的最大值为0，因此$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$的最大值为第一项，即$f(\mathbf{x})$。${\min }_{\mathbf{x}}{\max }_{\lambda ,\nu ,{\lambda }_i⩾0}L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$等价于${\min }_{x}f(\mathbf{x})$。也就是4-17的优化目标。
2. 如果$\mathbf{x}$不是可行解，即存在$g_i(\mathbf{x})>0$或者$h_i(\mathbf{x})\ne 0$，因为${\lambda }_i⩾0$，$\nu$没有限制，因此$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$的最大值是$+\infty$（令${\lambda }_i$取$+\infty$或$\nu$取$sign(h_i(\mathbf{x}))\infty$，无法求解最小值。

证毕。

我们已经证明4-19的优化问题与4-17的优化问题等价，下面介绍拉格朗日对偶。

首先定义4-19所示的优化问题为原问题，原问题首先固定$\mathbf{x}$，找到使得$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$最大的$\lambda ,\mathbf{\nu }$，然后求使得$L(\mathbf{x},{\mathbf{\lambda }}_{\ast },{\mathbf{\nu }}_{\ast })$最小的$\mathbf{x}$。原问题的对偶问题定义如下： $$\underset{\lambda ,\nu ,{\lambda }_i⩾0}{\max }\underset{\mathbf{x}}{\min }L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })\text{\hspace{1em}(4-20)}$$即首先固定$\lambda ,\mathbf{\nu }$，找到使得$L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$最小的$\mathbf{x}$，然后求使得$L(\mathbf{x},{\mathbf{\lambda }}_{\ast },{\mathbf{\nu }}_{\ast })$最大的$\lambda ,\mathbf{\nu }$。

在后面支持向量机的学习中我们可以发现，对偶问题往往比原问题更容易求解。

下面介绍关于原问题和对偶问题的弱对偶定理（Weak Duality），如下：$$\underset{\mathbf{\lambda },\mathbf{\nu },{\lambda }_i⩾0}{\max }\underset{\mathbf{x}}{\min }L(\mathbf{x},\mathbf{x},\mathbf{\lambda },\mathbf{\nu })⩽\underset{\mathbf{x}}{\min }\underset{\mathbf{\lambda },\mathbf{\nu },{\lambda }_i⩾0}{\max }L(\mathbf{x},\mathbf{\lambda },\mathbf{\nu })$$即对偶问题目标函数的值小于等于原问题目标函数的值。证明起来也比较容易，设${\mathbf{x}}_1,{\mathbf{\lambda }}_1,{\mathbf{\nu }}_1$是原问题的最优解，${\mathbf{x}}_2,{\mathbf{\lambda }}_2,{\mathbf{\nu }}_2$是对偶问题的最优解，容易有 ： $$L\left({\mathbf{x}}_1,{\mathbf{\lambda }}_1,{\mathbf{\nu }}_1\right)⩾L\left({\mathbf{x}}_1,{\mathbf{\lambda }}_2,{\mathbf{\nu }}_2\right)⩾L\left({\mathbf{x}}_2,{\mathbf{\lambda }}_2,{\mathbf{\nu }}_2\right)$$证毕。

强对偶问题

即便是有了弱对偶定理，我们可以保证对偶问题的解对应的目标函数是原问题目标函数值的下界，但是依然无法准确求出原问题的解和对应的目标函数值。强对偶（Strong Duality）帮我们解决了这个问题，强对偶的定义是原问题和对偶问题有相同的最优解。

首先介绍强对偶的一个充分条件-Slater条件，它指出：一个凸优化问题如果存在一个解使得所有不等式约束都是严格满足的，也就是$g_i(\mathbf{x})⩽0$中等号总是不满足，那么在不等式约束趋于内至少存在一个可行点$\left({\mathbf{x}}^{\ast },{\mathbf{\lambda }}^{\ast },{\mathbf{\nu }}^{\ast }\right)$既是对欧问题的最优解，也是原问题的最优解。

这里我们不再对Slater条件进行进一步的讨论，但是补充一下什么事凸优化问题，见板书。

关于强对偶问题的例题见课件。

KKT条件

KKT条件（Karush-Kuhn-Tucker）给出了带约束优化问题取极值的一阶必要条件。对于4-17表示的优化问题，对应的拉格朗日函数为公式4-18，则最优解$\mathbf{x}$满足4-21所述条件： $$\{\begin{array}{l}\nabla f+{\sum }_j^p{\lambda }_j\nabla h_i+{\sum }_i^q{\mu }_i\nabla g_i=0\\ h_j=0,j=1,2,\cdots ,n\\ g_i\le 0,i=1,2,\cdots ,m\\ {\mu }_i\ge 0\\ {\mu }_i{g}_i=0\end{array}\text{\hspace{1em}(4-21)}$$下面分别对这五个方程进行介绍：

1. 第一个方程说明目标函数的梯度是等式和不等式约束梯度的线性组合（参见上述讨论）；
2. 第二个方程对应原优化问题的等式约束；
3. 第三个方程对应原优化问题的非等式约束；
4. 第四个方程式引入拉格朗日乘子（此处成为KKT乘子）需要满足的条件，成为对偶松弛条件；
5. 第五个方程成为互补松弛条件，如果对于第$k$个不等式约束，对应的$u_i$为0，则该条件称为非活跃约束，最优解不在该条件的边界上；如果对于第$k$个不等式约束，对应的$u_i$不为0，则$g_i=0$，则该条件称为活跃约束，最优解在该条件的边界上。

对于一般优化问题，KKT条件是去机制的必要条件，如果最优化问题是一个凸优化问题，则KKT条件是取得极值的充要条件。

补充知识完毕。

模型求解

我们回到问题的求解上来。考虑硬间隔支持向量机的优化目标公式4-8：
$$\begin{array}{l}{\min }_{w,b}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,N\end{array}\text{\hspace{1em}(4-8)}$$首先观察优化问题的目标函数是一个二次函数，二次函数的黑塞矩阵正定，为凸函数，约束条件是仿射函数，可行域为凸集，因此这是一个典型的凸优化问题；由于硬间隔支持向量机假设数据是线性可分的，因此一定存在解，假设${\mathbf{w}}_0$和${\mathbf{b}}_0$是一组解，有$y_i\left({\mathbf{w}}_0^{\mathrm{T}}{\mathbf{x}}_i+b_0\right)⩾1$，则一定有$\alpha {\mathbf{w}}_0$和$\alpha {\mathbf{b}}_0$是另一组解，$\alpha$不为0。且当$\alpha >1$时，不等式约束严格满足。 因此该优化问题满足Slater条件，强对偶关系成立。

容易写出它对应的拉格朗日函数： $$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-\sum _{i=1}^N{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)\text{\hspace{1em}(4-22)}$$
根据拉格朗日乘子法，最优化问题应该是：
$$\underset{\mathbf{w},b}{\min }\underset{{\alpha }_i⩾0}{\max }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(4-23)}$$注意$L(\mathbf{w},b,\mathbf{\alpha })$是一个关于$\alpha$的一次方程，如果先以$\alpha$为自变量求梯度，令梯度为0向量的话，无法求解处最优的$\alpha$。由于强对偶成立，因此求解其对偶问题： $$\underset{{\alpha }_i⩾0}{\max }\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(4-24)}$$令梯度为0向量，有${\nabla }_{w}L=\mathbf{w}-{\sum }_{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i=0$和$\frac{\partial L}{\partial b}={\sum }_{i=1}^N{\alpha }_i{y}_i=0$，求解得到： $$\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(4-25)}$$ $$\mathbf{w}=\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i\text{\hspace{1em}(4-26)}$$
将4-25和4-26带入到朗格朗日函数中可以消除$\mathbf{w}$和$b$：$$\begin{array}{l}L=\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\sum }_{i=1}^N{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)=\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\sum }_{i=1}^N\left({\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+{\alpha }_i{y}_{i}b-{\alpha }_i\right)\\ =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\sum }_{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i-{\sum }_{i=1}^N{\alpha }_i{y}_{i}b+{\sum }_{i=1}^N{\alpha }_i=\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\mathbf{w}}^{\mathrm{T}}{\sum }_{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i-b{\sum }_{i=1}^N{\alpha }_i{y}_i+{\sum }_{i=1}^N{\alpha }_i\\ =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+{\sum }_{i=1}^N{\alpha }_i=-\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+{\sum }_{i=1}^N{\alpha }_i=-\frac{1}{2}{\left({\sum }_{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i\right)}^{\mathrm{T}}\left({\sum }_{j=1}^N{\alpha }_j{y}_j{\mathbf{x}}_j\right)+{\sum }_{i=1}^N{\alpha }_i\end{array}\text{\hspace{1em}(4-27)}$$
同时别忘了我们还有两个约束条件，即所有的${\alpha }_i$大于等于0以及我们得到的关系式4-25。最后我们的优化问题变成： $$\begin{array}{l}{\min }_{\alpha }\left(\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j-{\sum }_{i=1}^N{\alpha }_i\right)\\ {\alpha }_i⩾0，i=1,2,\dots N\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}\text{\hspace{1em}(4-28)}$$

对于熟悉优化问题的同学们而言，这是一个典型的凸二次优化问题，可以用一些求解QP问题的套件来具体求解，也可以直接使用SMO算法求解（SMO算法挖坑）。

求出$\alpha$后，可以利用公式4-26求解$\mathbf{w}$，再利用互补松弛条件找到一个不为0的${\alpha }_i$求$b$（可以求得$b=y_p-{\mathbf{w}}^T{\mathbf{x}}_p$，其中${\mathbf{x}}_p$是第$p$个${\alpha }_p$不为0的数据）。

模型解析

通过对硬间隔支持向量机的图形化分析，我们知道对分类起到关键作用的实际上是“支持向量”，也就是前面图中虚线上的数据点。在实际的模型求解中，这些数据也起到至关重要的作用。

考虑互补松弛条件${\alpha }_i\left(1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\right)=0$，实际上有大量的${\alpha }_i$求解出来是0，这些${\alpha }_i$对应的数据点就是“支持向量”以外的点，这些点对模型的求解没有作用。换句话说，不管添加多少个数据点，只要这些数据点不是支持向量，SVM的最优解不变。

上述特性通过求解过程也很容易理解。因为我们对$\mathbf{w}$的求解依赖的是公式4-26，而公式4-26中的${\alpha }_i$为0对应的$y_i{\mathbf{x}}_i$起不到任何作用。对$b$的求解也是如此。

此外，我们发现，新的优化问题跟原问题相比，变量的个数为$N$个，约束条件有$N+1$个，$N$是数据 的数量，也就是说现在问题的求解难度只跟数据集大小有关，跟自变量（或者经过特征转换过的自变量）的空间大小无关。

软间隔支持向量机

模型形式

硬间隔支持向量机有一个基本假设是数据是线性可分的，这在实际情况中很难出现，因此需要对其进行改进。

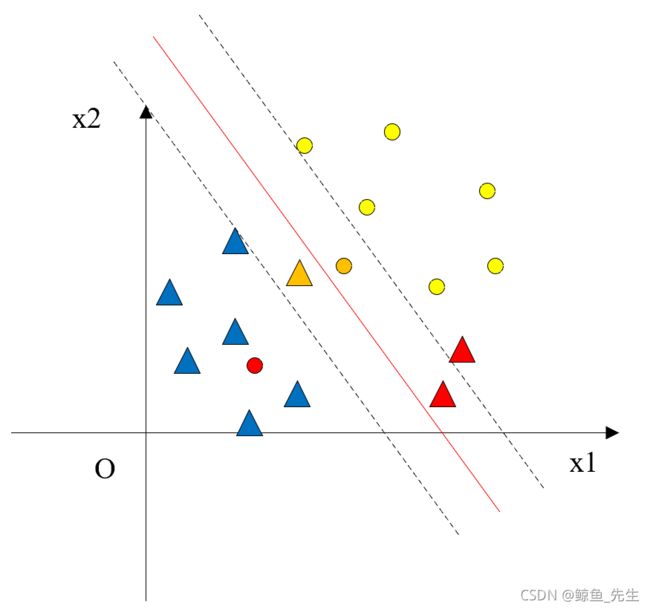
软间隔支持向量机设置松弛变量，以此来放松对线性可分的限制。在硬间隔支持向量机中，我们假设支持向量到超平面的距离为1，因此有约束条件：$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1$，设松弛变量${\xi }_i$是一个大于等于0的实数，那些支持向量以外的点（图4-5中的橙色点）以及不能被正确分类的点（图4-6中的红色点）到超平面的距离记作$1-{\xi }_i$，同时我们应该在目标函数中对不能正确划分的数据进行惩罚，惩罚系数为$C>0$。于是，新的优化问题变成了如下形式： $$\begin{array}{l}{\min }_{\mathbf{w},b,\mathbf{\xi }}\left(\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+C{\sum }_{i=1}^N{\xi }_i\right)\\ y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ {\xi }_i⩾0,i=1,\cdots ,N\end{array}\text{\hspace{1em}(4-29)}$$

另外需要说明的是，松弛变量和折页损失函数效果相同，后者可以写作：

可以证明，4-29所示的优化问题满足Slater条件，强对偶关系成立。因此可以使用拉格朗日对偶方法，求解如下最优化问题：
$$\underset{{\alpha }_i⩾0,{\xi }_i⩾0,\mathbf{\beta }}{\max }\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha },\mathbf{\xi },\mathbf{\beta }))\text{\hspace{1em}(4-30)}$$其中拉格朗日函数：

$$L(\mathbf{w},b,\mathbf{\alpha },\mathbf{\xi },\mathbf{\beta })=\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1+{\xi }_i\right)-\sum _{i=1}^N{\beta }_i{\xi }_i\text{\hspace{1em}(4-31)}$$

模型求解

首先求以$\mathbf{w}$和$b$为自变量的最小值，求梯度令梯度为0可得： $${\nabla }_{\mathbf{w}}L=\mathbf{w}-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i=0\frac{\partial L}{\partial b}=\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(4-32)}$$
因此有： $$\sum _{i=1}^N{\alpha }_i{y}_i=0\mathbf{w}=\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{x}}_i\text{\hspace{1em}(4-33)}$$
将4-33代入到拉格朗日函数中有：$$\begin{array}{rl}L(\mathbf{w},b,\mathbf{\alpha },\mathbf{\xi },\mathbf{\beta })& =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1+{\xi }_i\right)-\sum _{i=1}^N{\beta }_i{\xi }_i\\ & =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\beta }_i{\xi }_i-\sum _{i=1}^N{\alpha }_i{\xi }_i-\sum _{i=1}^N{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)\\ & =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+\sum _{i=1}^N\left(C-{\alpha }_i-{\beta }_i\right){\xi }_i-\sum _{i=1}^N\left({\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+{\alpha }_i{y}_{i}b-{\alpha }_i\right)\\ & =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-\sum _{i=1}^N{\alpha }_i{y}_i{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b+\sum _{i=1}^N{\alpha }_i+\sum _{i=1}^N\left(C-{\alpha }_i-{\beta }_i\right){\xi }_i\\ & =\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}-{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+\sum _{i=1}^N{\alpha }_i+\sum _{i=1}^N\left(C-{\alpha }_i-{\beta }_i\right){\xi }_i=-\frac{1}{2}{\mathbf{w}}^{\mathrm{T}}\mathbf{w}+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j+\sum _{i=1}^N{\alpha }_i+\sum _{i=1}^N\left(C-{\alpha }_i-{\beta }_i\right){\xi }_i\end{array}\text{\hspace{1em}(4-34)}$$
通过比较可以看出，4-34比4-27仅仅多了最后一项${\sum }_{i=1}^N\left(C-{\alpha }_i-{\beta }_i\right){\xi }_i$，我们可以继续对$\mathbf{\xi }$求梯度，可以得到：
$$\frac{\partial L}{\partial {\xi }_i}=C-{\alpha }_i-{\beta }_i=0\text{\hspace{1em}(4-35)}$$
同时别忘了我们的两个约束条件，即所有的${\alpha }_i$大于等于0以及我们得到的关系式4-25，另外还有公式4-35以及${\beta }_i⩾0$，可以得到$0⩽{\alpha }_i⩽C$。于是，最终的优化问题变成： $$\begin{array}{l}{\min }_{\alpha }\left(\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j-{\sum }_{i=1}^N{\alpha }_i\right)\\ 0⩽{\alpha }_i⩽C，i=1,2,\dots N\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}\text{\hspace{1em}(4-36)}$$

模型解析

优化问题4-36进一步可以写成矩阵形式： $$\begin{array}{l}{\min }_{\alpha }\frac{1}{2}{\mathbf{\alpha }}^{\mathrm{T}}\mathbf{Q}\mathbf{\alpha }-{\mathbf{e}}^{\mathrm{T}}\mathbf{\alpha }\\ 0⩽{\alpha }_i⩽C\\ {\mathbf{y}}^{\mathrm{T}}\mathbf{\alpha }=0\end{array}\text{\hspace{1em}(4-37)}$$
其中$Q_{ij}=y_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j={\left(y_1{\mathbf{x}}_1,\cdots ,y_N{\mathbf{x}}_N\right)}^T\left(y_1{\mathbf{x}}_1,\cdots ,y_N{\mathbf{x}}_N\right)$，很明显是一个半正定矩阵，它也是目标函数的黑塞矩阵，黑塞矩阵半正定，说明目标函数是一个凸函数，约束条件都是线性的，可行域是凸集，因此该问题是凸优化问题，在最优点处 满足KKT条件。
原问题的两个不等式约束必须满足互补松弛性，即： $$\begin{array}{rl}{\alpha }_i\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1+{\xi }_i\right)=0,& i=1,\cdots ,N\\ {\beta }_i{\xi }_i=0,& i=1,\cdots ,N\end{array}\text{\hspace{1em}(4-38)}$$同时还要满足原问题中的约束条件，即： $$\begin{array}{l}{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ {\xi }_i⩾0,i=1,\cdots ,N\end{array}\text{\hspace{1em}(4-39)}$$以及KKT乘子大于等于0： $$\begin{array}{rl}{\alpha }_i⩾0,& i=1,\cdots ,N\\ {\beta }_i⩾0,& i=1,\cdots ,N\end{array}\text{\hspace{1em}(4-40)}$$以及梯度为0给我们的信息：$${\alpha }_i+{\beta }_i=C\text{\hspace{1em}(4-41)}$$
结合4-38到4-41，我们分三种情况对模型进行解析。

1. 当${\alpha }_i=0$时，$\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1+{\xi }_i\right)$没有约束，${\beta }_i=C$；因为${\beta }_i{\xi }_i=0$，所以${\xi }_i=0$，结合4-39的第一个不等式推导出$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1$。也就是说，当${\alpha }_i=0$时，对应的数据到超平面的点比支持向量点到超平面的距离（即1）要大，这些数据点对模型没有影响，为自由向量。
2. 当${\alpha }_i=C$时，根据互补松弛性的第一个公式，有$\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1+{\xi }_i\right)=0$，即$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)=1-{\xi }_i$；根据公式4-41， ${\beta }_i=0$，互补松弛性对${\xi }_i$没有约束，约束条件中有${\xi }_i⩾0$，因此$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)=1-{\xi }_i⩽1$，也就是说，当${\alpha }_i=C$时，对应的数据到超平面的点比支持向量点到超平面的距离（即1）要小，这些数据点时违反硬间隔不等式约束的数据点（即不能不线性划分的点）。
3. 当$0⩽{\alpha }_i⩽C$时，我们既有$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1$又有$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)=1-{\xi }_i⩽1$，因此$y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)=1-{\xi }_i=1$。也就是说，当$0⩽{\alpha }_i⩽C$时，对应的数据点是支持向量。

支持向量机的核技巧

模型形式

上文提到，对于硬间隔支持向量机，利用拉格朗日对偶方法优化问题可以写成4-28，对于软间隔支持向量机，利用拉格朗日对偶方法优化问题可以写成4-36。

同时，值得注意的是即便不使用拉格朗日对偶方法，原优化问题也是一个凸优化问题，一样可以借助一些QP套件进行求解。之所以使用拉格朗日乘子对偶方法，是想将原来$p+1$个自变量、$N$个约束条件的优化问题转化成$N$个自变量、$N+1$个约束条件的优化问题。这样一来，优化问题的复杂度就跟输入空间的大小无关，只跟样本数量有关了。这样的方法特别适合输入空间比较大的优化问题，尤其是在原输入空间线性不可分的情况下，需要首先进行特征转换，转换后的新特征空间的维度有可能会很大甚至是无穷维。

然而，我们观察使用拉格朗日对偶之后的优化问题，尽管需要优化的变量数量有变化，但是依然没法彻底解决维度太大带来的计算问题。因为在计算${\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$（${\mathbf{x}}_i$可以属于原来的输入空间，也可以属于新的特征空间），即计算输入向量的内积时，还是受数据维度的影响。如果输入向量是经过特征转换后的特征空间，这个空间可能很大，计算起来会非常麻烦。而对于大部分问题，一般来说使用特征转换后效果会要好得多。因此最好有一种方法能够帮助我们彻底摆脱计算内积时特征空间维度的影响。于是，核技巧横空出世！

核技巧的基本思想是：既然计算输入变量的内积时会受到特征转换后特征空间维度的影响，那么可以想办法将特征转换和内积计算结合起来。我们一起来看一下这样的思路是否可行。

我们将特征转换后的特征向量记作${\mathbf{z}}_i,i=1,2,\dots ,N$,特征转换函数记作$\Phi \left(\cdot \right)$，即${\mathbf{z}}_i=\Phi \left({\mathbf{x}}_i\right)$，特征向量的内积${\mathbf{z}}_i^T{\mathbf{z}}_j=\Phi \left({\mathbf{x}}_i\right)\Phi \left({\mathbf{x}}_j\right)$。我们以硬间隔支持向量机对应的优化问题4-28进行示范，软间隔支持向量机的形式可以由其推而广之。

硬间隔支持向量机的优化问题用矩阵形式可以写成：$$\begin{array}{l}{\min }_{\alpha }\frac{1}{2}{\mathbf{\alpha }}^{\mathrm{T}}\mathbf{Q}\mathbf{\alpha }-{\mathbf{e}}^{\mathrm{T}}\mathbf{\alpha }\\ {\alpha }_i⩾0,i=1,2,\dots N\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}\text{\hspace{1em}(4-42)}$$

其中$Q_{ij}=y_i{y}_j\Phi {\left({\mathbf{x}}_i\right)}^T\Phi \left({\mathbf{x}}_j\right)={\left(y_1\Phi \left({\mathbf{x}}_i\right)\cdots ,y_N\Phi \left({\mathbf{x}}_i\right)\right)}^T\left(y_1{\mathbf{x}}_1,\cdots ,y_N\Phi \left({\mathbf{x}}_N\right)\right)$。

定义核函数，将特征转换和特征转换后的内积两个步骤合并：$$K_{\Phi }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\Phi ({\mathbf{x}}_i{)}^T\Phi \left({\mathbf{x}}_j\right)\text{\hspace{1em}(4-43)}$$

于是有： $$Q_{ij}=y_i{y}_j{K}_{\Phi }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\text{\hspace{1em}(4-44)}$$接下来需要找到合适的核函数，$K_{\Phi }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$使得相关运算不再受特征空间的维度影响。

我们不妨先来看看一个特例，对于二阶多项式的特征转换，我们将原始的输入变量${\mathbf{x}}_i$映射到二阶多项式对应的空间：$${\Phi }_2({\mathbf{x}}_{\mathbf{i}})=\left(1,{\mathbf{x}}_{i1},{\mathbf{x}}_{i2},\dots ,{\mathbf{x}}_{ip},{\mathbf{x}}_i^2,{\mathbf{x}}_{i1}{\mathbf{x}}_{i2},\dots ,{\mathbf{x}}_{i1}{\mathbf{x}}_{ip},{\mathbf{x}}_{i2}{\mathbf{x}}_{i1},{\mathbf{x}}_{i2}^2,\dots ,{\mathbf{x}}_{i2}{\mathbf{x}}_{ip},\dots ,{\mathbf{x}}_{ip}^2\right)\text{\hspace{1em}(4-45)}$$

那么我们有：

$$\begin{array}{rl}{K}_{\Phi }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\Phi {\left({\mathbf{x}}_i\right)}^T\Phi \left({\mathbf{x}}_j\right)& =1+\sum _{d=1}^p{x}_{id}{x}_{jd}+\sum _{d=1}^p\sum _{d=1}^p{x}_{id}{x}_{id}{x}_{jd}{x}_{jd}\\ & =1+\sum _{i=1}^p{x}_{id}{x}_{jd}+\sum _{d=1}^p{x}_{id}{x}_{jd}\sum _{d=1}^p{x}_{id}{x}_{jd}\\ & =1+{{\mathbf{x}}_{\mathbf{i}}}^T{\mathbf{x}}_{\mathbf{j}}+\left({{\mathbf{x}}_{\mathbf{i}}}^T{\mathbf{x}}_{\mathbf{j}}\right)\left({{\mathbf{x}}_{\mathbf{i}}}^T{\mathbf{x}}_{\mathbf{j}}\right)\end{array}\text{\hspace{1em}(4-46)}$$
二次多项式转换后的特征空间维度是$p^2+1$， 经过核函数处理后，相关的运算只与$\mathbf{x}$（维度是$p$）有关，而与特征空间的维度无关。

也就是说，经过核函数的运算后，尽管原始输入空间使用了特征转换，但是矩阵$Q$各元素的相关运算$Q_{ij}=y_i{y}_j{K}_{\Phi }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$却不再跟特征空间有关。我们使用核函数实现了上面的要求。

二次多项式特征转换更一般的形式可以写成：$${\Phi }_2({\mathbf{x}}_{\mathbf{i}})=\left(1,\sqrt{2\gamma }{\mathbf{x}}_{i1},\dots ,\sqrt{2\gamma }{\mathbf{x}}_{id},\gamma {\mathbf{x}}_{i1}^2,\dots ,\gamma {\mathbf{x}}_{ip}^2\right)\text{\hspace{1em}(4-47)}$$对应的核函数为： $$K_2\left({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}}\right)={\left(1+\gamma {{\mathbf{x}}_{\mathbf{i}}}^T{\mathbf{x}}_{\mathbf{j}}\right)}^2\text{\hspace{1em}(4-48)}$$

称为二次多项式核，其中$\gamma >0$。已经证明二次多项式核是符合我们要求的核函数，推而广之，更高次的多项式核也是符合我们要求的核函数，感兴趣的同学们可以自行证明。n次多项式核的形式可以统一写成：$$K_n\left({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}}\right)={\left(\zeta +\gamma {{\mathbf{x}}_{\mathbf{i}}}^T{\mathbf{x}}_{\mathbf{j}}\right)}^n\text{\hspace{1em}(4-48)}$$其中$\gamma >0,\zeta$