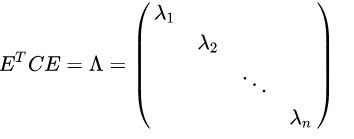山东大学机器学习实验7 PCA+ SVM 人脸识别

山东大学机器学习实验7 PCA+ SVM 人脸识别

实验学时： 4 实验日期：2021.12.6

实验题目：PCA in Face Recognition

实验目的

In this exercise, you will learn how to apply PCA to the images to reduce data dimension, and then use SVM classifier to realize face recognition.

使用PCA实现图像的降维，并且应用SVM实现人脸识别

实验环境

软件环境

​ Windows 10 + Matlab R2020a

硬件环境

​ CPU: Intel® Core™ i5-8300H CPU @ 2.30GHz 2.30 GHz

​ GPU: NVIDIA GeForce GTX 1050Ti

实验步骤与内容

了解PCA

Dimensionality Reduction

如何从一个高维数据，学习到一个有用的低维数据呢？Called "Feature Learning"即学习一个更好的，经常是更小维度的representation of the Data

个人理解就是：有些东西是一个D维度来表示的，但是你通过降维，提取出关键的维度，使用一个K(K < D) 的维度也能很好地表现出这个东西。而低维度的数据在很多时候能够有加速运算等优点

并且Fewer Dim 意味着Less chances of over fitting 且 Better generalization

Linear Dimensionality Reduction

一种简单的方法是进行一个线性降维

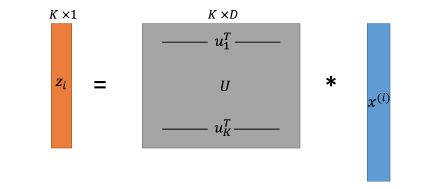
从一个D维的X 映射到 K维度的Z 只需要通过一个K X D 维度的矩阵即可

个人理解其实就是类似于DNN里面最基础的全连接层，进行一个线性D -> K的线性加权，反之对应于矩阵U的参数，也能线性分解，得到D维度的X

But 如何去学一个最好的矩阵$U$使得我们降维之后的误差最小呢？

引入了一个主成分分析原则PCA

Principle Component Analysis

"Best" 可以从两个方面衡量 一个是Max Variance 另外一个是Smallest Reconstruction Error 即要么你在构建这几个主要维度的时候能够让

​ 为什么方差大好呢？想想坐标轴，如果方差最大的那个方向，往往是最有代表性的， 蕴含信息最多的。所以其实PCA也就是每次找一个方差最大的方向作为一个轴或者叫 Feature

​ 另外是重建之后的error最小。因为将为必然会造成数据信息的损失，这点能够体现在 reconstruction里面，所以重建效果最好的也是最好的。而且可以证明两者等价。

然后通过计算协方差矩阵，得到协方差矩阵的特征值以及特征向量，选择特征值最大的K个特征即可得到Best Matrix U 实现降维

协方差矩阵(三维为例)

或者计算方式如下：

Algorithm Steps：

1. 中心化、去平均值
2. 计算协方差矩阵，因为去中心化了，所以此时$S=\frac{1}{N}{\sum }_{i=1}^N{x}^{(i)}{\left(x^{(i)}\right)}^T$
3. 用特征值分解的方法求协方差矩阵的特征值以及特征向量
4. 根据特征值Sort，选取最大的K个，将他们的特征向量组成特征向量矩阵$U$
5. 计算将为之后的数据:$Z=U^{T}X$

此外，得到协方差矩阵的特征值方法有

• 特征值分解协方差矩阵
• 奇异值分解协方差矩阵(SVD分解)

SVM多分类原理

基础的SVM是一个二分类器，如何实现多分类呢？

one-against-one

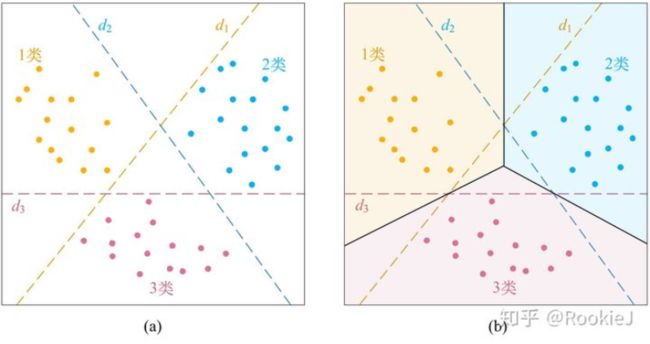
设训练集数据共 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6TvJosFK-1639294057575)(https://www.zhihu.com/equation?tex=M)] 个类，one-against-one方法是在每两个类之间都构造一个binary SVM。以下图(a)为例，共三类(二维)数据，虚线 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JV52hE6L-1639294057576)(https://www.zhihu.com/equation?tex=d_{12})] 表示1类和2类数据之间的binary SVM的决策边界， [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pkgZElxw-1639294057577)(https://www.zhihu.com/equation?tex=d_{13})] 表示1类和3类之间的决策边界， [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Y0V8fpcd-1639294057578)(https://www.zhihu.com/equation?tex=d_{23})] 则表示2类和3类之间的决策边界。

对于测试数据，则采用投票策略进行分类

• 每个binary SVM根据其决策函数对新数据$X_{new}$​有一个预测(投票)，

  以 i 类和j类之间的binary SVM为例，若对 $X_{new}$ 的预测为i类，则i类得票加1；反之j类加一票。

• 最终得票最多的类别就是对 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-moFh34yI-1639294057579)(https://www.zhihu.com/equation?tex=\mathbf+x_{new})] 的预测

One-Against-All

对于每一个类，将其作为+1类，而其余M-1个类的所有样本作为-1类，构造一个binary SVM。如下图(a)所示，对于黄点所示的1类，将2类和3类都当成-1类，构造binary SVM，其决策边界为$d_1$;对于蓝点所示的2类，则将1类和3类都当成-1类，构造binary SVM，其决策边界为$d_2$;同理得到$d_3$

对于测试数据$X_{new}$ ，M个决策函数M个输出。选择概率最大的作为分类结果。

---

Task Description

The images are organized in 40 directories, each of which
consists of 10 images. Note that, in each directories, the images are taken from
the same person.

图像数据被组织再40个目录里面，每个目录都是一个人，由10张图片组成

To construct a set of training data, we randomly pick 5∼7 images from each
categories, while leaving the others as test data. Please first apply PCA to the
images to reduce data dimension, and then use SVM classifier to realize face
recognition. Specifically, for a given face image, find who is in the image

为了构建一组训练数据，我们从每个目录(人)中随机选取 5∼7 个图像，而将其他类别作为测试数据。先将 PCA 应用到 图像降维，然后使用SVM分类器实现人脸识别。具体来说，对于给定的人脸图像，找出图像中的人。

Report the classification accuracy based on your training data by varying parameter K(i.e., the number of projections in PCA)

根据训练数据以及不同的参数K，报告你的分类准确率

---

What I do

在本实验中我实现了：

• 在PCA中，求解特征值和特征向量用了特征值分解的方法
• 在PCA中，针对于数据的 “小样本” 数据的特点，即特征数远大于样本数目，求解特征值和特征向量用了SVD的方法，大大加快了速度。
• 在SVM中，使用了一对多的分类方式来实现多分类
• 在SVM中，使用了一对一的分类方式，在相同的降维的维度下，获得到准确率往往优于大于等于一对多的情况
• 找出了误分类的部分图片，并且直观展示。

Experiment

Analyze Data

分析数据发现，每一张image都是一个灰度图,Size = 112 X 92

即可以认为每条数据的feature 都是 112 X 92 = 10304 维度的，所以维度很高，需要降维，使用PCA降维

除此之外一共有40个人， 每人10张picture，也就是大概有200-280条训练数据，120-200条测试数据

数据预处理

这里是把400个数据条目都读入，然后把图片flatten 即: 112 * 92 = 10304，整个data size = 400 * 10304

加载数据即首先随机产生一个5~7的随机数来作为训练数据的比例，然后在每个人脸文件夹中随机抽取对应个数的照片作为训练数据，其余的作为测试数据。

其余的数据处理：

• 在一对多时，

编写基础PCA

整体思路

​ 首先中心化，然后求协方差矩阵，size = N * N, N = 10304

​ 然后利用matlab提供的eig函数求解协方差矩阵特征值以及特征向量，这一步是PCA中 代价最高的步骤，然后对特征值排序，取对应的前K个特征向量构成变换矩阵U size = N*K

​ 最后用原始数据 * U 得到新数据，size = M * K，然后按照比例划分对应的训练集以及 测试集即可。

优化点：

​ 因为最初不知道K的大体范围是多少，我以为需要达到1000~10000的size，为了解决这个问题，采用一个比例，即排名前几的特征值的总和达到所有特征值的和的比例满足条件，例如我设置了

$rates=[0.1,0.3,0.4,0.5,0.6,0.7,0.75,0.8,0.85,0.9];$ 只要满足要求就记录下K值，结果发现K的值非常非常小，如下：
$K=[1,2,4,6,10,19,27,38,55,82];$

几乎一百以内就可以了，比例以及K值关系如下图：

所以就可以根据这几个K值去进行降维，然后SVM

最初的PCA 代码见最后。

---

编写SVM(1 To 1 & 1 To All)

One To All:

思路简述：四十个人，即四十个类别，每次找一个类别标为正类，其余的都认为是负样本，然后进行SVM的二分类训练，训练一个针对于这个类别的W和B的值。

然后进行测试：测试的时候，对于一个给定的测试数据test_xi，需要对他进行40次计算，然后求作为正样本的值最大的那一个类别，即为这个数据的label。

然后和真正的Label，求交集，得到个数，推出准确率。

One To One:

思路简述：四十个人，即四十个类别，每次选两个类别即 $C_{40}^2=780$个pair，对每一个Pari都计算一个W和B，得到一个W的矩阵以及一个B的矩阵。

然后进行测试：测试的时候，对于一个给定的测试数据test_xi，需要对他进行40次计算，然后求作为正样本的值最大的那一个类别，即为这个数据的label。

然后和真正的Label，求交集，得到个数，推出准确率。

对于按比例求得的K 分别进行一对多和一对一的多分类，得到的结果如下图：

Rate	K	准确率(One To All)	准确率(One To One)
10%	K = 1	5.50%	20.00%
30%	K = 2	22.50%	52.50%
40%	K = 4	42.50%	95.50%
50%	K = 6	70.00%	99.50%
60%	K = 10	95.50%	100%
70%	K = 19	100%	100%
75%	K = 27	100%	100%
80%	K = 38	100%	100%
85%	K = 55	100%	100%
90%	K = 82	100%	100%

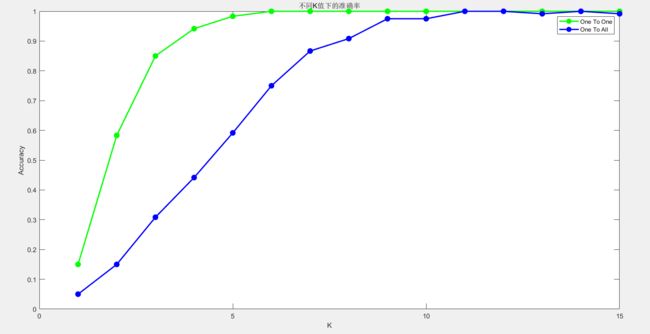
根据这个图就可以发现

• One To One的多分类效果好于One To All
• One To One在K=10所有就达到最好的效果了，而One To All 可能是在10-20之间

所以改变PCA的K值选择策略，不是按照比例填充K，而是直接进行赋K值

K = 1 : 1 : 15 即从1到15进行测试，得到的效果如下图

具体数据如下：

K	准确率(One To All)	准确率(One To One)
K = 1	5.00%	15.00%
K = 2	15.00%	58.33%
K = 3	30.83%	85.00%
K = 4	44.17%	94.17%
K = 5	59.17%	98.33%
K = 6	75.00%	100%
K = 7	86.67%	100%
K = 8	90.83%	100%
K = 9	97.50%	100%
K = 10	97.50%	100%
K = 11	100%	100%
K = 12	100%	100%
K = 13	99.17%	100%
K = 14	100%	100%
K = 15	99.17%	100%

找出部分误分类的人脸图像

根据分类结果，可以轻而易举的找出原始人脸图像以及被误认为的人脸的样子

输出信息以及图片如下：

Time Cost

时间效率是一个很大的因素，记录了一下PCA的时间，大概需要90~100s

统计时间花费均值如下：平均花费93s才能进行一次PCA降维

如果我要对多个K值进行计算并且加上SVM优化的话，时间将会达到数小时，那么如何提高时间效率呢？

SVD求解特征值特征向量

具体的数学推导，在结论分析与体会中

大概的思路是：对于小样本数据即feature个数远大于数据个数，(10304 >> 400)的这种情况，如果使用SVD进行一个求解，那么将会大大加快速度。

即协方差矩阵改为$X^{\prime }\ast X$ 得到的$SIZE=400\ast 400$然后同样是eig求解该协方差矩阵的特征值以及特征向量，然后利用SVD的左奇异向量以及奇异值(此时认为奇异值等于特征值)求解出变换矩阵$SIZE=N\ast K$，然后元数据和变化矩阵相乘，得到变换之后的数据即$SIZE=M\ast K$

而中间相比于原来的$10304\ast 10304$矩阵的特征值的求解来说$400\ast 400$的求解快了接近$10^5$的数量级！！！球的平均时间如下：

得到的准确率图如下：

具体数据如下：

K	准确率(One To All)	准确率(One To One)	TimeCost
K = 1	5.00%	17.50%
K = 2	16.67%	53.33%
K = 3	35.83%	86.67%
K = 4	42.50%	97.50%
K = 5	56.67%	98.33%
K = 6	70.83%	100%
K = 7	75.83%	100%
K = 8	93.33%	100%
K = 9	96.67%	100%
K = 10	98.33%	100%
K = 11	100%	100%
K = 12	99.17%	100%
K = 13	100%	100%
K = 14	98.33%	100%
K = 15	99.17%	100%

找出部分误分类的人脸如下图：有些确实是比较像的(红框标注)

除此之外，对比一对一以及一对多的SVM，虽然一对一的效果好，但是对应的花费时间也是比较长的，记录如下，可以看到一对一的时间总是比一对多久。

至此全部结束~ ~ ~

---

结论分析与体会

SVD奇异值分解与PCA的关系

假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。P即变换矩阵。

上面维度不变

如果要降维，将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，把这个称为feature的压缩。用数学语言表示就是

​ SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量

SVD式子:

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U’

其他降维方法

还有很多降维方法，比如SVD奇异值分解 FA因子分析法 ICA独立成分分析法等…

Multi-Class SVM

除了基础的一对一 以及 一对多分类之外，还有一种只需求解一个优化问题的多分类方法。

引用自：

J. Weston and C. Watkins. 1998. Multi-class support vector machines. Technical Report CSD-TR-98-04, Department of Computer Science, Royal Holloway, University of London.

J. Weston and C. Watkins. Support vector machines for multi-class pattern recognition In Proceedings of the Seventh European Symposium on Artificial Neural Networks, April 1999.

这种方法类似于一对多，构造M个二类的决策函数，其中第m个函数${\omega }_m^T\varphi (x_t)+b_m$ 将第m类和其余类分开。形成的优化问题如下：

解这个优化问题得到全部M个决策函数

决策函数为：

数学理论

补充一点数学理论：

原始数据矩阵对应的协方差矩阵$C$ 与 变换之后的$Z=U^{T}X$对应的协方差矩阵$D$之间的关系

$D=\frac{1}{m}Z{Z}^T=\frac{1}{m}(U^{T}X)(U^{T}X{)}^T=U^{T}CU$

此外$C$是一个对称矩阵，有如下性质

1. 实对称矩阵不同特征值对应的特征向量必然正交
2. 设特征向量 $\lambda$ 重数为 r，则必然存在 r 个线性无关的特征向量对应于$\lambda$ ，因此可以将这 r 个特征向量单位正交化。

由上面两条可知，一个 n 行 n 列的实对称矩阵一定可以找到 n 个单位正交特征向量，设这 n 个特征向量为 $e_1,e_2...e_n$ 按列组成矩阵$E=(e_1,e_2...e_n)$

这时，所需要的对角矩阵就是之前的$U^T=E^T$

即协方差矩阵的特征向量单位化后代的矩阵

不足之处

• 如果想要测试多个K的PCA效果，假设使用特征值分解的情况，其实更好的方案是，使用一次eig，求出特征值之后，再针对不同的K进行处理，即无需每次K单独进行一次Eig求特征值。 但是整体效果是一样的。
• 代码封装已经比较好了，但是为了不同的测试，可能存在一些冗余

实验源代码

lab72.m 主函数

%% ================读取数据================
clear,clc;
% 随机选择取5--7张作为训练集
train_percent = randi([5,7]);% 随机一个5-7
train_percent= 7;
% ===初始参数===
dimx = 112;dimy = 92;
class_num = 40;
% ===数据读取=== Dim : (class_num*train_percent,dimx*dimy)
[train_datas,test_datas] = LoadData(train_percent,dimx,dimy,class_num);
%rates = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.75,0.8,0.85,0.9];
%% 大概算了一下 K = 1 2 2 4 6 10 19 27 38 55 82
% 不用rate 直接用K 因为121 在K=10就100%了 所以这次选择从 1 : 15 15次
K = linspace(1,15,15);

%% ================PCA降维================
Datas = [train_datas;test_datas];
misclasses11 = cell(15,1);
misclasses1all = cell(15,1);
SVMFLAGs=[1,0];
sumt = 0;
t1end = zeros(15,1);
t2end = zeros(15,1);
for SVMFLAGi = 1:2 
    for i = 1:15
        t0 = tic;
        %[new_train_datas,new_test_datas] = MyPCA2(Datas,K(i),train_percent,class_num);
        [new_train_datas,new_test_datas] = MyPCASVD(Datas,K(i),train_percent,class_num);
        sumt = sumt + toc(t0);
        %% ================SVM多分类================
        %SVMFLAG = 0;% 0:1对多SVM 多分类 
        %SVMFLAG = 1;% 0:1对1SVM 多分类
        SVMFLAG = SVMFLAGs(SVMFLAGi);
        if SVMFLAG == 1
            t1 = tic;
            [misclasses11{i},accuracy11(i)] = MySVM1(new_train_datas,new_test_datas,class_num,K(i),train_percent);
            t1end(i) = t1end(i) + toc(t1);
        else
            t2 = tic;
            [misclasses1all{i},accuracy1all(i)] = MySVM0(new_train_datas,new_test_datas,class_num,K(i),train_percent);
            t2end(i) = t2end(i) + toc(t2);
        end
    end
    
end
avg_timecost= sumt/30;
fprintf('使用特征值分解的PCA的平均时间花费为:%f s\n',avg_timecost);

%% 准确率
figure
plot(K,accuracy11,'.-','LineWidth',2,'color','g','MarkerSize',30)
hold on
plot(K,accuracy1all,'.-','LineWidth',2,'color','b','MarkerSize',30)
xlabel('K')
ylabel('Accuracy')
title('不同K值下的准确率(使用PCA-SVD)')
legend('One To One','One To All');
%% 对比SVM 的效率
figure
plot(K,t1end,'.-','LineWidth',2,'color','g','MarkerSize',30)
hold on
plot(K,t2end,'.-','LineWidth',2,'color','b','MarkerSize',30)
xlabel('K')
ylabel('TimeCost')
title('不同K值下的SVM代价时间(使用PCA-SVD)')
legend('One To One','One To All');

%% 找几张错误的图片
ori = misclasses{4}{1}(:,1);
pre = misclasses{4}{1}(:,2);
difference = find(ori~=pre);
for i=1:length(difference)
    fprintf('误认为S%d 是 S%d\n',ori(difference(i)),pre(difference(i)));
    path = ['orl_faces\s'];
    personid= randi([1,10]);
    filename1 = [path,num2str(ori(difference(i))),'\',num2str(personid),'.pgm'];
    ori_img = double(imread(filename1));
    filename2 = [path,num2str(pre(difference(i))),'\',num2str(personid),'.pgm'];
    pre_img = double(imread(filename2));
    figure
    subplot(2,1,1);
    imshow(uint8(ori_img)),title('原人脸图像');
    subplot(2,1,2);
    imshow(uint8(pre_img)),title('被误认为的人脸')
end

基础PCA的代码 以比例定K值

MyPCA.m

%% ================PCA降维================
function [newtrainData,newtestData,K] = MyPCA(Datas,rate,train_percent,class_num)
fprintf(' =======Do PCA Dimensionality Reduction...=======\n');
% Step 1: 中心化
    mean_val = mean(Datas);
    newData1 = Datas - mean_val;
% Step 2: 求协方差矩阵
    C = newData1'*newData1 / size(newData1,1);
% Step 3: 计算特征向量和特征值
    %[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V
    %其列是对应的右特征向量，使得 A*V = V*D。
    [V,D] = eig(C);
% Step 4: 排序
    [val,order] = sort(diag(-D));% 降序
    eigenvalue = diag(D); % 得到特征值
    eigenvector = V(:,order); % 特征向量
    eigenvalue = eigenvalue(order); % 特征值也重新排序
% Step 5: 取前K行，组成矩阵U 然后计算
    % 原特征相当于有112*92=10304个特征
    % 可以选K=[1000 3000 5000 6000 7000 8000 9000 10000]
    % 此处 使用rate比例 来动态定义K
    K = 0;
    sumeigenval = sum(eigenvalue);
    for i = 1:length(eigenvalue)
        rating = sum(eigenvalue(1:i,1),1)/sumeigenval;
        if rating >= rate
            K = i;
            break;
        end
    end
    fprintf(' ================Rate = %f================\n',rate);
    fprintf(' =============This Turn K = %d.==============\n',K);
    U = eigenvector(:,1:K);
    % M*K = M*N * N*K
    newData = newData1 * U;
    newtrainData = newData(1:train_percent*class_num,:);
    newtestData = newData(train_percent*class_num+1:400,:);
    fprintf(' ==========Dimension From 10304 Lower To %d==========\n',K);
    fprintf(' =============== Done PCA ===============\n');
end

使用具体K值的PCA代码

MyPCA2.m

%% ================PCA2降维================
function [newtrainData,newtestData,K] = MyPCA2(Datas,K,train_percent,class_num)
fprintf(' =======Do PCA Dimensionality Reduction...=======\n');

% Step 1: 中心化
    mean_val = mean(Datas);
    newData1 = Datas - mean_val;
% Step 2: 求协方差矩阵
    C = newData1'*newData1 / size(newData1,1);
% Step 3: 计算特征向量和特征值
    %[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V
    %其列是对应的右特征向量，使得 A*V = V*D。
    [V,D] = eig(C);
% Step 4: 排序
    [val,order] = sort(diag(-D));% 降序
    eigenvalue = diag(D); % 得到特征值
    eigenvector = V(:,order); % 特征向量
    eigenvalue = eigenvalue(order); % 特征值也重新排序
% Step 5: 取前K行，组成矩阵U 然后计算
    % 原特征相当于有112*92=10304个特征
    fprintf(' =============This Turn K = %d.==============\n',K);
    U = eigenvector(:,1:K);
    newData = newData1 * U;
    newtrainData = newData(1:train_percent*class_num,:);
    newtestData = newData(train_percent*class_num+1:400,:);
    fprintf(' ==========Dimension From 10304 Lower To %d==========\n',K);
    fprintf(' =============== Done PCA ===============\n');
    
end

使用SVD的PCA

MyPCASVD.m

%% ================PCA2降维================
function [newtrainData,newtestData,K] = MyPCASVD(Datas,K,train_percent,class_num)
fprintf(' =======Do PCA Dimensionality Reduction(Based on SVD)...=======\n');
Datas = Datas';
t0 = tic;
[NN,Train_NUM]=size(Datas);
% Step 1: 中心化
    mean_val = mean(Datas,2);
    newData1 = Datas - mean_val*ones(1,Train_NUM);
% Step 2: 求协方差矩阵  ！这里改了！
    C = newData1'*newData1 / Train_NUM;
% Step 3: 计算特征向量和特征值
    %[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V
    %其列是对应的右特征向量，使得 A*V = V*D。
    %[V,D] = eig(C);
    
    % 使用SVD分解
    %[V,D,U] = svd(C,'econ');
    [V,S]=Find_K_Max_Eigen(C,K);
    %Vector: 400*K value:1*K
    % 左奇异向量 以及 奇异值 M*K
    disc_value=S;% 
    disc_set=zeros(NN,K);
    
    qiyizhi = ones(K,K);
    for i = 1:K
        qiyizhi(i,i) = disc_value(i);
    end
    
    newData1=newData1/sqrt(Train_NUM-1);
    
    %disc_set = 10000 * 8  data 10000 * 400
    for k=1:K
        % 映射回feature N*M   *  M*K  ->  N * K
        disc_set(:,k)=(1/sqrt(disc_value(k)))*newData1*V(:,k);
    end
    
% Step 5: 取前K行，组成矩阵U 然后计算
    % 原特征相当于有112*92=10304个特征
    fprintf(' =============This Turn K = %d.==============\n',K);
    newData = newData1'*disc_set;
    newtrainData = newData(1:train_percent*class_num,:);
    newtestData = newData(train_percent*class_num+1:400,:);
    fprintf(' ==========Dimension From 10304 Lower To %d==========\n',K);
    fprintf(' =============== Done PCA ===============\n');
    toc(t0);
end

MySVM1.m

实现一对一的SVM多分类

%% ================1to1 SVM多分类================
% 1对1 即任意选出两个类作为二分类的SVM训练集
% 分别贴上+-标签，训练 C40 2 = 40*39/2 = 780次
function [misclass,hit_rate] = MySVM1(train_X,test_X,class_num,k,train_percent)
    % Step 1: 标签分配 
    tp = train_percent;
    other = 10 - train_percent;
    train_times = class_num*(class_num-1)/2;
    data1 = cell(train_times,1);
    data2 = cell(train_times,1);
    index = 1;
    OneOneLabels = zeros(train_times,2);
    for i = 1:39
            for j = i+1:40
                % 成对放进元组里面，并且对应进行记录
                data1{index,1} = [[train_X(i*tp-(tp-1):i*tp,:),ones(tp,1)];[train_X(j*tp-(tp-1):j*tp,:),-ones(tp,1)]];
                data2{index,1} = [[test_X(i*other-(other-1):i*other,:),ones(other,1)];[test_X(j*other-(other-1):j*other,:),-ones(other,1)]];
                OneOneLabels(index,1) = i;
                OneOneLabels(index,2) = j;
                index = index + 1;
            end
    end
    fprintf(' =======Strat Training...=======\n');
    % Step 2: 训练
    A = zeros(train_times,2*tp);
    W = zeros(train_times,size(train_X,2));
    B = zeros(train_times,1);
    for i = 1:train_times
       svm = MysvmTrain(data1{i,1}(:,1:k),data1{i,1}(:,k+1),1);
       A(i,:) =  svm.a';
       for j = 1:size(train_X,2)
          W(i,j) = sum(A(i,:)'.*data1{i,1}(:,k+1).*data1{i,1}(:,j));
       end
       B(i,1) = sum(svm.Ysv-svm.Xsv*W(i,:)')/svm.svnum;
    end
    fprintf(' =======Training Finish=======\n');
    % Step 3: 测试
    fprintf(' =======Strat Testing...=======\n');
    labels_num = zeros(size(test_X,1),train_times);
    for i = 1:train_times
       labels_num(:,i) = (test_X*W(i,:)')'+B(i,1); 
    end
    % 分类结果
    labels_svm = zeros(40,39);
    for i = 1:40
         labels_svm(i,:) = find(OneOneLabels(:,1)==i | OneOneLabels(:,2)==i);
    end
    %统计每一类在各个分类器分类正确率、个数，投票方案
    Predict_Labels = zeros(size(test_X,1),1);
    for i = 1:size(test_X,1)
        VoteCounts = zeros(40,1);
        for j = 1:40
           for m = 1:39
               if labels_num(i,labels_svm(j,m)) > 0 && OneOneLabels(labels_svm(j,m),1) == j
                   VoteCounts(j,1) = VoteCounts(j,1) + 1;
               elseif labels_num(i,labels_svm(j,m)) < 0 && OneOneLabels(labels_svm(j,m),2) == j
                   VoteCounts(j,1) = VoteCounts(j,1) + 1;
               end
           end  
        end
        [~,index] = max(VoteCounts);
        Predict_Labels(i,1) = index;
    end
    Ori_Labels = zeros(size(test_X,1),1);
    for i = 1:40
       Ori_Labels((i-1)*other+1:(i-1)*other+other,1) = i; 
    end
    hit = find(Ori_Labels==Predict_Labels); % 160*1全是label
    hit_rate = length(hit)/size(test_X,1);
    % 找出误分类的
    miss = find(Ori_Labels~=Predict_Labels);
    % 记录误分类
    misclass = cell(1,1);
    misclass{1} = [Ori_Labels,Predict_Labels];
    fprintf(' =======Test Finish!=======\n');
    fprintf(' =======Accuracy = %f=======\n',hit_rate);
end
% 测试集的标签看比例就能推出来

MySVM0.m

实现一对多的SVM多分类

%% ================1to多 SVM多分类================
% 1对多 即任意选出一个类进行训练 这类是正其余都是负
% 训练 40次
function [misclass,hit_rate] = MySVM0(train_X,test_X,class_num,k,train_percent)
% Step 1: 
    class_nums = 40;
    data1 = cell(class_nums,1);
    data2 = cell(class_nums,1);
    for i = 1:class_nums
       data1{i,1} = LabelData(i,train_X,7);
       data2{i,1} = LabelData(i,test_X,3);
    end
% Step 2: 训练
    A = zeros(class_nums,size(train_X,1));
    W = zeros(class_nums,size(train_X,2));
    B = zeros(class_nums,1);
    for i = 1:class_nums
       svm = MysvmTrain(data1{i,1}(:,1:k),data1{i,1}(:,k+1),1);
       A(i,:) =  svm.a';
       for j = 1:size(train_X,2)
          W(i,j) = sum(A(i,:)'.*data1{i,1}(:,k+1).*data1{i,1}(:,j));
       end
       B(i,1) = sum(svm.Ysv-svm.Xsv*W(i,:)')/svm.svnum;
    end
% Step 3 测试
    labels_num = zeros(size(test_X,1),class_nums);
    for i = 1:class_nums
       labels_num(:,i) = (test_X*W(i,:)')'+B(i,1); 
    end
    predict_labels = zeros(size(test_X,1),1);
    % 转化为标签的具体整数值
    for i = 1:size(test_X,1)
        [~,index] = max(labels_num(i,:));
        predict_labels(i,1) = index;
    end
    ori_labels = zeros(size(test_X,1),1);
    %有规律的换算过去，得到测试集合的标签
    for i = 1:class_nums
       ori_labels((i-1)*3+1:(i-1)*3+3,1) = i; 
    end
    hit = find(ori_labels==predict_labels); % 160*1全是label
    hit_rate = length(hit)/size(test_X,1);
    % 找出误分类的
    miss = find(ori_labels~=predict_labels);
    % 记录误分类
    misclass = cell(1,1);
    misclass{1} = [ori_labels,predict_labels];
    fprintf(' =======Test Finish!=======\n');
    fprintf(' =======Accuracy = %f=======\n',hit_rate);
    
end

LoadData.m

进行加载数据的函数

%% ================读取数据的函数================
function [train_datas,test_datas] = LoadData(train_percent,dimx,dimy,class_num)
    % train_datas: 40*7,112*92 
    fprintf(' Train_Percent = %d%%\n',train_percent*10);
    fprintf(' ================Loading Datas...================\n');
    path = ['orl_faces\'];
    test_percent = 10-train_percent;
    for i = 1 : class_num
        personid = ['s',num2str(i)];
        index = randperm(10);
        % train Data
        %fprintf(' ================Loading Training Datas...================\n');
        for j = 1:train_percent
            filename = [path,personid,'\',num2str(index(j)),'.pgm'];
            img = double(imread(filename));
            % 这里存取没用张量，而是每张图片flatten存
            train_datas(train_percent*(i-1)+j,:) = reshape(img,1,dimx*dimy);
        end
        % test Data
        
        for j = 1:test_percent
            filename = [path,personid,'\',num2str(index(j)),'.pgm'];
            img = double(imread(filename));
            % 这里存取没用张量，而是每张图片flatten存
            test_datas(test_percent*(i-1)+j,:) = reshape(img,1,dimx*dimy);
        end
    end
    fprintf(' ================Loading Finish!================\n');
end

LabelData.m

用在一对多里面标注Label

%% ================标注Data的label================
function data = LabelData(index,X,n)
    len = size(X,1);
    % 
    if index == 1
        % 把1-7 表正，其余的标-1
        data = [[X(1:n,:),ones(n,1)];[X(n+1:len,:),-ones(len-n,1)]];
    else
        % 找到对应样本的位置，选出来标1 其余的标-1，分了三段
        data = [[X(1:n*(index-1),:),-ones(n*(index-1),1)];[X(n*index-n+1:n*index,:),ones(n,1)];[X(n*index+1:len,:),-ones(len-n*index,1)]];
    end
end

Find_K_Max_Eigen.m

找K个特征值以及特征向量

function [Eigen_Vector,Eigen_Value]=Find_K_Max_Eigen(Matrix,Eigen_NUM)

[NN,NN]=size(Matrix);
[V,S]=eig(Matrix); %Note this is equivalent to; [V,S]=eig(St,SL); also equivalent to [V,S]=eig(Sn,St); %

S=diag(S);
[S,index]=sort(S);

Eigen_Vector=zeros(NN,Eigen_NUM);
Eigen_Value=zeros(1,Eigen_NUM);

p=NN;
for t=1:Eigen_NUM
    Eigen_Vector(:,t)=V(:,index(p));
    Eigen_Value(t)=S(p);
    p=p-1;
end

MysvmTrain.m

用于训练一个二分类SVM模型的函数

%% ================SVM的训练函数================
function svm  = MysvmTrain(X,Y,C)
    %二次规划用来求解问题，使用quadprog
    options = optimset;
    options.largeScale = 'off'; %LargeScale指大规模搜索，off表示在规模搜索模式关闭
    options.Display = 'off'; %表示无输出
    n = length(Y);  
    %使用线性核   
    H = (Y.*X)*(Y.*X)';
    H=(H+H')/2;
    f = -ones(n,1); %f'为1*n个-1
    A = [];
    b = [];
    Aeq = Y'; 
    beq = 0;
    lb = zeros(n,1); 
    ub = C*ones(n,1);
    a0 = zeros(n,1);  % a0是解的初始近似值
    a = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
    epsilon = 1e-9;
    sv_label = find(abs(a)> epsilon);
    svm.sva = a(sv_label);
    svm.Xsv = X(sv_label,:);
    svm.Ysv = Y(sv_label);
    svm.svnum = length(sv_label);
    svm.a = a;
end

en_NUM);

p=NN;
for t=1:Eigen_NUM
Eigen_Vector(:,t)=V(:,index§);
Eigen_Value(t)=S§;
p=p-1;
end

> MysvmTrain.m
>
> 用于训练一个二分类SVM模型的函数

```matlab
%% ================SVM的训练函数================
function svm  = MysvmTrain(X,Y,C)
    %二次规划用来求解问题，使用quadprog
    options = optimset;
    options.largeScale = 'off'; %LargeScale指大规模搜索，off表示在规模搜索模式关闭
    options.Display = 'off'; %表示无输出
    n = length(Y);  
    %使用线性核   
    H = (Y.*X)*(Y.*X)';
    H=(H+H')/2;
    f = -ones(n,1); %f'为1*n个-1
    A = [];
    b = [];
    Aeq = Y'; 
    beq = 0;
    lb = zeros(n,1); 
    ub = C*ones(n,1);
    a0 = zeros(n,1);  % a0是解的初始近似值
    a = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
    epsilon = 1e-9;
    sv_label = find(abs(a)> epsilon);
    svm.sva = a(sv_label);
    svm.Xsv = X(sv_label,:);
    svm.Ysv = Y(sv_label);
    svm.svnum = length(sv_label);
    svm.a = a;
end