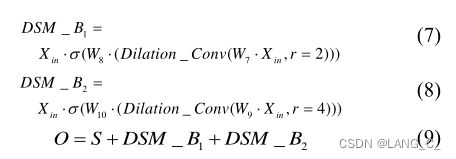【论文精读】TMI2022.FCP-Net

语义分割论文

论文：FCP-Net: A Feature-Compression-Pyramid Network Guided by Game-Theoretic Interactions for Medical Image Segmentation

论文地址：https://ieeexplore.ieee.org/document/9667534

Published in: IEEE Transactions on Medical Imaging ( Volume: 41, Issue: 6, June 2022)

---

目录

语义分割论文

摘要

尚未解决的问题：

一、主要亮点

二、网络结构

1.FCP-Net

2.An embedded feature ensemble for separable convolution module

3. Dilated spatial mapping and channel attention modules 

4. Branch layer fusion module 

5. Decoder

四、损失函数

1.合作博弈：夏普利值（shapley value）性质与算法

2.这部分其实没有看太懂，唉。。。

三、实验部分

1. 消融实验​

---

摘要

医学图像分割是疾病诊断和分析的关键步骤，具有重要的临床应用价值。DeepLabv3+等深度神经网络方法已成功应用于医学图像分割，但多层特征很少无缝集成到不同的注意机制中，很少有研究探讨医学图像分割与分类任务之间的交互作用。

在此，我们提出了一个由博弈论相互作用和混合损失函数(HLF)引导的特征-压缩-金字塔网络(FCP-Net)用于医学图像分割。该方法由分割分支、分类分支和交互分支组成。在编码阶段，利用嵌入特征集成、膨胀空间映射与通道注意(DSMCA)和分支层融合三个模块，提出了一种新的分割分支策略。

这些模块可以有效提取空间信息，高效识别各种特征之间的空间相关性，并充分集成不同分支的多接收野特征。在解码阶段，利用DSMCA模块和多尺度特征融合模块建立多个跳接增强融合特征。引入分类和交互分支是为了探索分类信息任务对分割任务的潜在好处。我们从博弈论的角度进一步探讨了分割和分类分支的相互作用，并设计了一个HLF。基于该HLF，分割、分类和交互分支可以在整个训练过程中相互协作学习和教授，从而利用分割任务和分类任务之间的联合信息，提高泛化性能。利用包括ISIC2017、ISIC2018、REFUGE、Kvasir-SEG、BUSI和PH2在内的多个数据集对所提出的模型进行了评估，结果证明其与其他最先进的技术相比具有竞争力。

---

尚未解决的问题：

1. attention权重的稳定性以及注意机制与残差块之间的互补性尚未被充分利用，以缓解病灶分割的挑战；
2. 多层次特征很少完美地集成到不同的注意机制中，这可能导致低层次特征的冗余使用；
3. 为了学习额外的特征表示，提高模型的泛化能力，以往的多任务学习方法通常使用特征通过模块或两步训练策略，这增加了模型的参数和推理的复杂性。

一、主要亮点

• 特征压缩金字塔网络(FCP-Net)，由三个分支组成，如分割(主要分支)、分类和交互分支，来提取目标的空间信息、通道信息和多尺度信息
• 由博弈论相互作用和混合损失函数(HLF)指导，通过这种交互，不同分支可以在整个训练过程中相互协作学习和教授，从而利用分割任务和分类任务之间的联合信息，提高泛化性能。

二、网络结构

1.FCP-Net

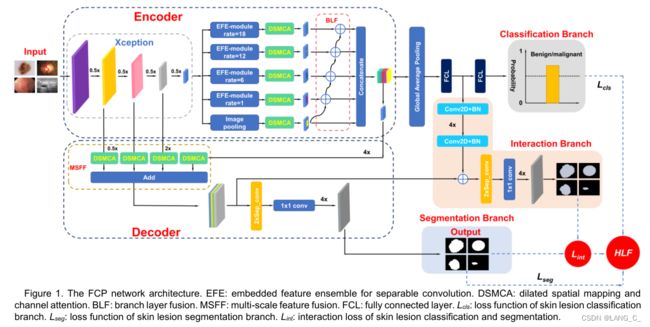
提出的FCP-Net由三个分支组成，分别是分割、分类和交互(见图1)。其中最主要的分支是用于医学图像分割的分割分支。分类分支和交互分支是辅助分支，用于探索分割和分类之间的交互作用。在分割分支中，编码器网络用于学习输入数据的潜在表示，解码器网络用于从编码器模块重建信息。本文提出了一种新的编码策略，包括EFE、DSMCA和BLF模块。这三个组件用于:

1. Embedded Feature Ensembles基于上下文信息和权重的特征响应自适应重新校准：采用EFE模块自适应捕获卷积层信道之间的显式关系。通过使用轻量级注意机制，这是为了专注于有用的功能，同时抑制其他功能。
2. Dilated Spatial Mapping And Channel Attention捕捉不同特征之间的空间相关性，并将注意力集中在通道关系上，以提高性能：为了有效地提取和利用多尺度上下文信息。
3. Branch Layer Fusion分别对目标进行多分支信息集成：利用BLF模块集成不同分支间的多接收域信息。

在编码器网络的末端为分割分支添加分类分支。分类分支包括一个全局平均池化层、两个全连接层和一个激活函数，可以预测输入图像的良恶性。交互分支提供分类分支和分割分支之间的交互信息。如前所述，交互分支只在训练阶段使用。

2.An embedded feature ensemble for separable convolution module

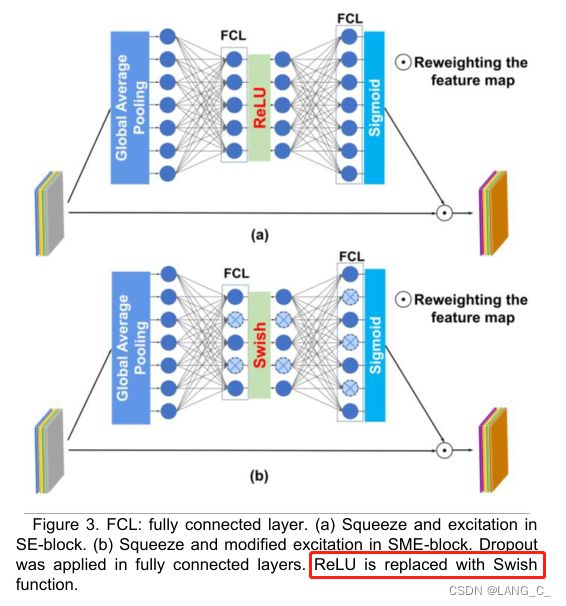
受SE网络的启发，提出通过一个注意力机制和残差块的EFE模块用来捕获卷积层通道之间的关系；第一个组件是深度可分离卷积，然后送入squeeze and multi-excitation (SME) 中，SME是通过改进SE获得的，用来自适应地捕获信道信息。

将激活函数改为Swish，然后在全连接层之后添加Dropout层，用于防止不同通道之间的复杂协同适应，从而促进每个通道自己编码有用的信息。SME块的数学表达式可以表示为:

Sep的可分离卷积的输出；

深度可分离卷积（Depthwise seperable convolution）

3. Dilated spatial mapping and channel attention modules 

这一模块用于捕获上下文信息并提取有用的特征，为了缓解多层次特征没有完美地融入到不同的注意力机制中。

文章说模块需要满足三个标准：

1. 一种多尺度融合方法，能够对多尺度信息进行集成，并学习聚集信息的非线性相互作用
2. 模块应该自适应地将局部特性与其全局依赖结合起来，比如通道注意力和位置注意力
3. 模块需要尽可能少的参数

然后提出了自己的DSMCA模块，一种结合通道和多感知场空间注意机制的结构

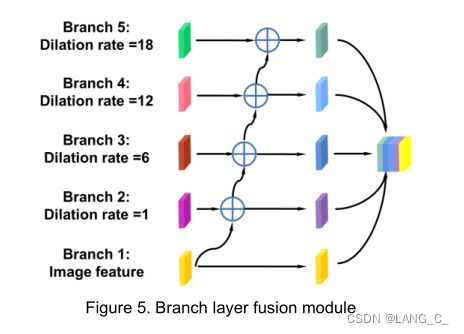
4. Branch layer fusion module 

作者为了提升不同大小病变的分割性能，使用了一个5分支融合模块来获取多感受野信息。将扩张率较大的分支与扩张率较小的分支合并以融合多范围上下文信息，融合通过“add”操作实现。

5. Decoder

之前的编码器解码器一般都是直接跳跃连接来提供信息，作者提出了一个MSFF模块来聚合多尺度上下文如上图，将四个尺度的特征由DSCMA模块独立细化通过不同的上下采样到同一尺度，进行相加操作。该模块的输出被传输到两个深度可分离的卷积层。然后进行第二次双线性上采样。与DeepLabv3+中简单的单级融合不同，MSFF模块的输入来自编码器网络中的四个不同阶段，我们在所有四个阶段都使用DSMCA模块，以专注于更多信息的功能。

四、损失函数

1.合作博弈：夏普利值（shapley value）性质与算法

游戏理论之Shapley Value（Shapley值）

2.这部分其实没有看太懂，唉。。。

三、实验部分

1. 消融实验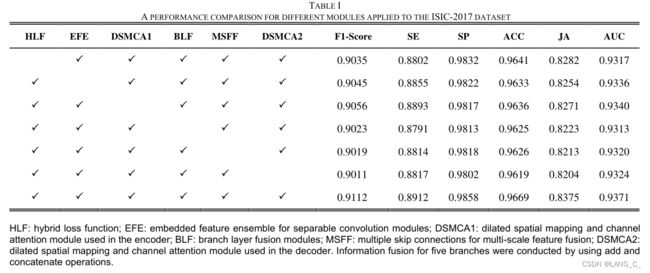

2.

• 需要注意的是，虽然SME板块起源于SE板块，但这两个板块有很大的不同。首先，SE块在第一密集层之后使用ReLU作为激活函数，但是ReLU在高层层的表现不是很好。然后我们用Swish激活函数替换它。其次，EFE模块的输入通道过多。SME有助于网络聚焦重要渠道，避免过拟合。在SME区块中，我们利用dropout在训练阶段随机丢弃一些通道，这样可以限制不同通道之间的交互，使得保留的通道中包含的信息更有利于模型的泛化。此外，我们还将SME块和残差块结合起来，以缓解注意力导致一些高频噪声传播到网络深层的问题。
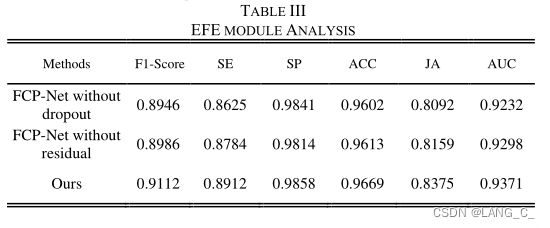
• 表III列出了这些方法的度量比较。可以看出，dropout或residual方法严重影响了模型的性能，我们提出的EFE模块比没有dropout或residual块的EFE模块性能要好得多。

  

• 如图所示的结果清楚地表明，当SME块有dropout层时，输入分辨率的变化对权重的MSD影响不大。这说明EFE模块保证了不同尺度目标注意权值的稳定性。
• DSMCA由SME块和多个扩张空间映射(DSM)块组成，该块可以沿着通道和空间分别对特征映射进行重新校准，然后合并输出。利用DSM块体探索不同特征之间的空间关系，重点关注感兴趣区域，并整合多尺度上下文信息。