浅析分支定界法在SLAM技术中的应用

参考文献

• SLAM主要步骤

• [概览]自动驾驶与AR增强现实中的关键技术：SLAM

• 浅谈国内SLAM技术发展现状

• SLAM技术的具体实现步骤

• 非常难得的 CMOS sensor 工作原理的深入技术科普

• 三步读懂CMOS图像传感器的工作原理

• 三角测距激光雷达原理

• SLAM在VR/AR领域重要吗？

• *深度优先搜索介绍

• *什么是整数规划？

• *分支定界法求整数规划

内容概要

• SLAM介绍
• Cartographer介绍
• 分支定界法讲解
• 应用演示
• 反思总结

SLAM介绍

• 经历了近30余年的发展，SLAM技术已日益成熟，从最早在军事中应用，如勇气号火星探测车，为了执行任务，借助SLAM技术在无法实时遥控的未知行星上来进行导航与避障。到如今，SLAM技术已广泛应用于民用场所，小到家庭中的扫地机，大到无人驾驶的汽车都应用了SLAM技术，以及在AR及VR领域均有SLAM技术的身影。

主要分类

• 视觉slam简称为Vslam

  • 眼睛是人类获取外界信息的主要来源。视觉SLAM也具有类似特点，它可以从环境中获取海量的、富于冗余的纹理信息，拥有超强的场景辨识能力。早期的视觉SLAM基于滤波理论，其非线性的误差模型和巨大的计算量成为了它实用落地的障碍。

  • 近年来，随着具有稀疏性的非线性优化理论(Bundle Adjustment)以及相机技术、计算性能的进步，实时运行的视觉SLAM已经不再是梦想。视觉SLAM的优点是它所利用的丰富纹理信息。例如两块尺寸相同内容却不同的广告牌，基于点云的激光SLAM算法无法区别他们，而视觉则可以轻易分辨。这带来了重定位、场景分类上无可比拟的巨大优势。

  • 同时，视觉信息可以较为容易的被用来跟踪和预测场景中的动态目标，如行人、车辆等，对于在复杂动态场景中的应用这是至关重要的。通过对比我们发现，激光SLAM和视觉SLAM各擅胜场，单独使用都有其局限性，而融合使用则可能具有巨大的取长补短的潜力。例如，视觉在纹理丰富的动态环境中稳定工作，并能为激光SLAM提供非常准确的点云匹配，而激光雷达提供的精确方向和距离信息在正确匹配的点云上会发挥更大的威力。而在光照严重不足或纹理缺失的环境中，激光SLAM的定位工作使得视觉可以借助不多的信息进行场景记录。

• 激光slam

  • 激光SLAM采用2D或3D激光雷达（也叫单线或多线激光雷达），2D激光雷达一般用于室内机器人上（如扫地机器人），而3D激光雷达一般使用于无人驾驶领域。激光雷达的出现和普及使得测量更快更准，信息更丰富。激光雷达采集到的物体信息呈现出一系列分散的、具有准确角度和距离信息的点，被称为点云。

  • 通常，激光SLAM系统通过对不同时刻两片点云的匹配与比对，计算激光雷达相对运动的距离和姿态的改变，也就完成了对机器人自身的定位。激光雷达测距比较准确，误差模型简单，在强光直射以外的环境中运行稳定，点云的处理也比较容易。同时，点云信息本身包含直接的几何关系，使得机器人的路径规划和导航变得直观。激光SLAM理论研究也相对成熟，落地产品更丰富。

传感器介绍

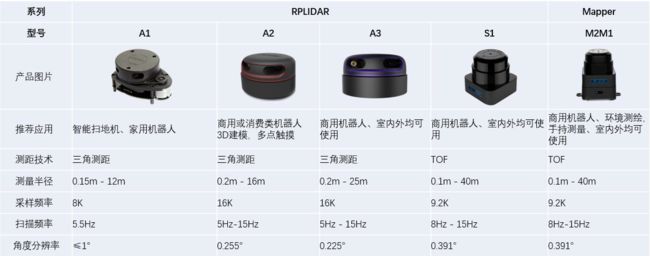
激光雷达传感器

• 采用了激光三角测距技术

  ​ 目前激光雷达的测量原理主要有脉冲法、相干法和三角法3种，脉冲法和相干光法对激光雷达的硬件要求高，但测量精度比激光三角法要高得多，故多用于军事领域。而激光三角测距法因其成本低，精度满足大部分商用及民用要求，故得到了广泛关注。

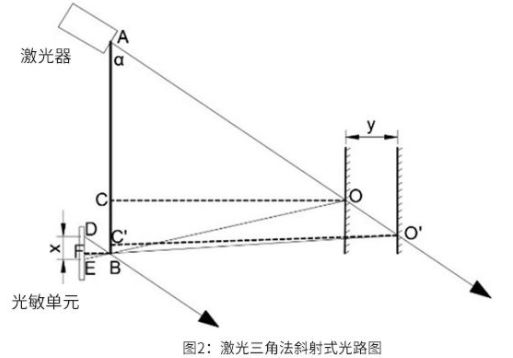
  ​ 激光三角测距法主要是通过一束激光以一定的入射角度照射被测目标，激光在目标表面发生反射和散射，在另一角度利用透镜对反射激光汇聚成像，光斑成像在CCD（Charge－coupled Device，感光耦合组件）位置传感器上。当被测物体沿激光方向发生移动时，位置传感器上的光斑将产生移动，其位移大小对应被测物体的移动距离，因此可通过算法设计，由光斑位移距离计算出被测物体与基线的距离值。由于入射光和反射光构成一个三角形，对光斑位移的计算运用了几何三角定理，故该测量法被称为激光三角测距法。按入射光束与被测物体表面法线的角度关系，激光三角测距法可分为斜射式和直射式两种。

  ​ 无论是直射式还是斜射式激光三角测距法，均可实现对被测物体的高精度、非接触测量，但直射式分辨率没有斜射式高。思岚科技的RPLIDAR系列激光雷达也采用了斜射式的激光三角测距法

  参考

  

​ 得到的数据是当前目标物体与雷达的距离值、夹角信息。

• 除配备激光雷达外，还需要机器人具有IMU（惯性测量单元）、里程计来为激光雷达提供辅助数据，否则SLAM系统也难以得到运行。总的来说，SLAM技术本身是一个对于外部系统有着多种依赖的算法，这是一个切实的工程问题。我们知道很多机器人，比如扫地机是不可能装一个PC进去的。为了让SLAM能在这类设备里运行，除了解决激光雷达成本外，还要对SLAM技术做出很好的优化。

• 三角测距原理介绍

• 发光部件：激光

• 感光部件：CMOS (Complementary Metal Oxide Semiconductor，互补金属氧化物场效应管)，光信号转电信号的传感器。

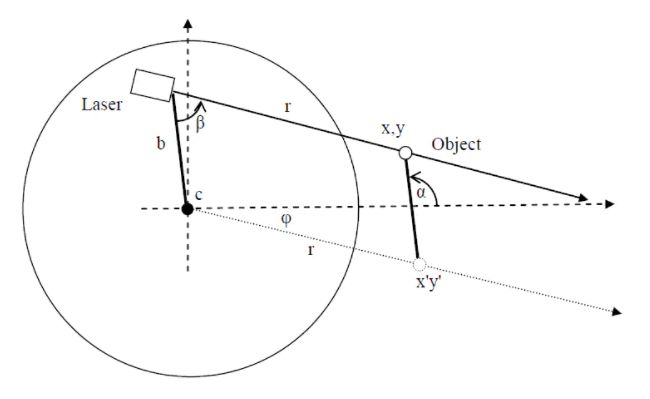
• 焦距是$f$，物体$Object$离平面的垂直距离是$q$，激光器和焦点间的距离是$s$，过焦点平行于激光方向的虚线，它跟$Imager$的交点位置一般是预先知道的（确定好$\beta$就知道了），物体激光反射后成像在$Imager$上的点位置离该处的距离为$X$。从图中很容易看出来，$s,d$,$\beta $ 组成的三角形跟 $X$,$f$ 组成的三角形是相似三角形，于是有：

  $$\begin{array}{r}\frac{f}{X}=\frac{q}{s},则q=\frac{f\times s}{x}\end{array}$$

  又由于：

  $$\begin{array}{r}sin\beta =\frac{q}{d},则d=\frac{q}{sin\beta }\end{array}$$

  最后得：

  $$\begin{array}{r}d=\frac{f\times s}{X\times sin\beta }\end{array}$$

• 因为f,s,beta都是预先可以已知的量，唯一需要测量的就是X，因此，测出X就测出了d，即得到物体离激光器的距离了。从图中可以轻易的看出，如果d的距离变短了，则X就会变大，d变大了，X就变小。从Imager测出X只要计算出得到的光斑的中心即可获得距离X。

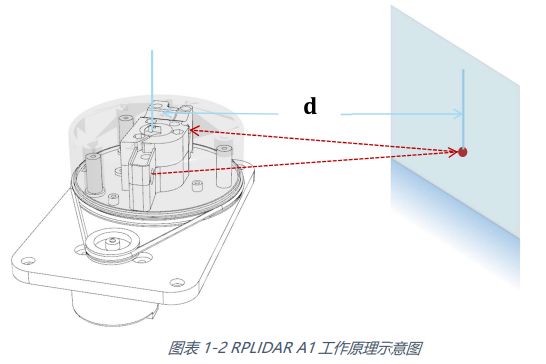
• 如何做成激光雷达

  将激光器和成像器固定在一起，做成一个固定的装置，然后旋转，即可获得周围360°的扫描结果了。

  

• 参数说明

  TOF(time-of-flight)

里程计

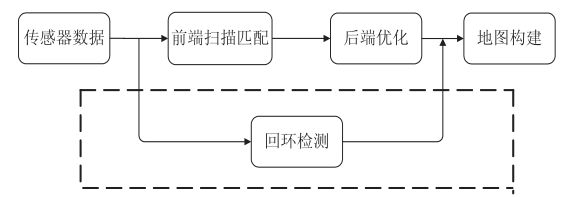
激光SLAM框架

• 传感器数据：图像、深度、距离等

  • 在视觉SLAM中主要为相机图像信息的读取和预处理。如果是在机器人中，还可能有码盘、惯性传感器(IMU)等信息的读取和同步。
  • 上图就是我们所说的点云，它只能反映机器人所在环境中的一个部分。而预处理主要是对激光雷达原始数据进行优化，并将一些有问题的数据进行剔除，或进行滤波。

• 前端扫描匹配：通过读取相邻两帧激光传感器扫描信息之间的关系来估计自身的位姿。

  • 匹配是很关键的一步，它的好坏将会直接影响SLAM构建的地图精度，其主要是把当前在局部环境上的一个点云数据，在已经建立地图上寻找到对应的位置。与我们玩的拼图游戏有点相似，就是在已经拼好的画面中找到相似之处，确定新的拼图该放的位置。而在SLAM过程中，需要将激光雷达当前采集的点云（红色部分）匹配拼接到原有地图中

    

• 后端优化：用来减少扫描匹配后产生的累积误差，并利用地图构建模块生成环境地图信息。

  • 后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在VO之后，又称为后端（Back End）

  • 数据融合与简单的贴图是有很大差异的，因为外部环境不仅有静态的，还有动态的，此时，如果在机器人旁边闯入了一只小狗，实际在进程数据融合的过程会更为复杂，需要用到很多概率算法，且处理难度很大。

    

• 回环检测：通过检测当前位置的估计值和历史位置的 估计值是否相同，来消除累积误差，从而减少地图漂移的现象。

  • 回环检测（Loop Closing）。回环检测判断机器人是否到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。

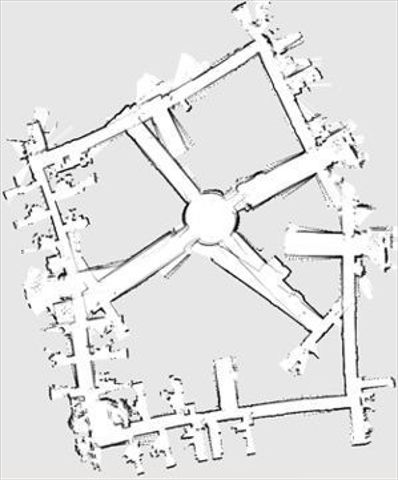
  • 举例来说，如果遇到回环问题，匹配算法不够优秀，或者在环境中存在很不巧的干扰，当机器人绕着环境走一圈后，便有可能出现原本应该闭合的一个环形走廊断开了。

    

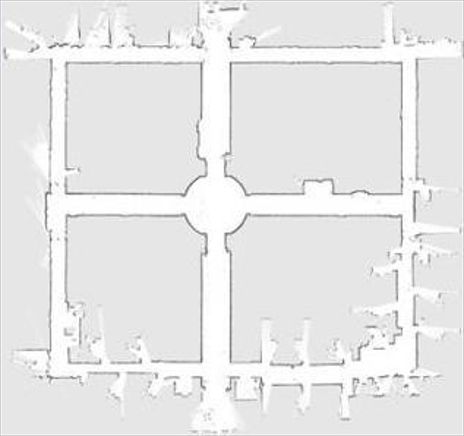
    比如正常地图应该这样：

    

  • 在环境较大场景，回环问题是不得不面对的，但现实总是不理想，即使拥有了高精度的激光雷达传感器，也难免存在一定误差，而回环的难点在于，在一开始的少许误差并不会被发觉，直到机器人走完一圈后，随着误差的不断累积，导致了环路无法闭合，出现这种情况一般很难回天。

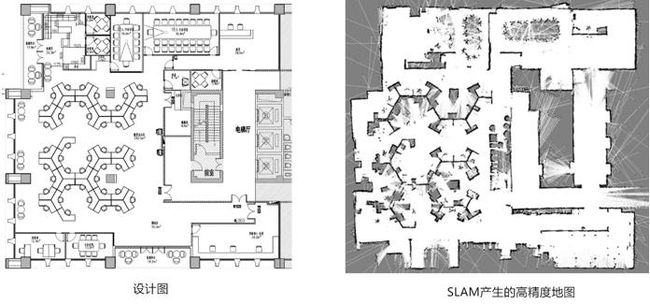
  • 以下是思岚科技员工在他们办公室进行的测试，当机器人已经绕场一周后，ROS构建的地图出现了中断，而利用SLAMWARE模块构建的地图是一个完美的闭环，它与思岚科技办公室的设计图完美重合。

    

• 地图构建：形成栅格地图、点云图

  • 它根据估计的轨迹，建立与任务要求对应的地图。

主要功能

• 激光建图
• 导航避障
• 建图与导航避障

落地项目

• 机器人(扫地机器人、市面上大部分能移动的机器人)

  

• 自动驾驶

  达摩院的快递车

  

• VR、AR

  定位、虚拟与现实的匹配

Cartographer介绍

Cartographer_Google的论文

• SLAM目前是一种实时建立地图的有效方式，实时生成可视化平面图有助于操作者评估捕获数据的质量和覆盖范围。构建便携式捕获平台需要在有限的计算资源下操作。我们介绍了在我们的背包地图平台中使用的方法，它实现了实时地图绘制和5厘米分辨率的环路闭合。为了实现实时闭环检测，我们使用了一种分支定界方法来计算scan-to-submap匹配作为约束，实验证明这个算法比较有竞争力。
• 传统的建图方式是通过CAD(计算机辅助设计)，通过激光卷尺来测量，但是这种方式很慢并且测量人员会先入为主的认为建筑物都是直的，不能很好的描述空间的真实情况。使用SLAM可以迅速而准确地测量大小和复杂程度的建筑物，而手动测量则需要更长数量级的时间。
• SLAM在这一领域的应用并不是一个新的想法，也不是本文的重点。相反，本文的贡献是一种新的方法，以减少计算回环检测要求的激光距离数据。这种技术使我们能够绘制非常大的楼层，数万平方米，同时为运营商提供充分优化的实时结果。

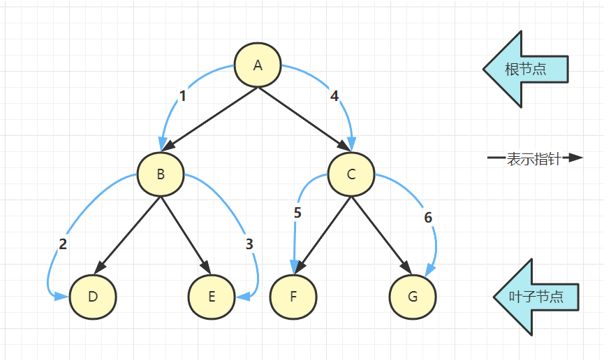
其主要思想是将可能的子集表示为树中的节点，其中根节点表示所有可能的解，在我们的例子中是W。每个节点的子节点构成其父节点的一个分区，因此它们一起表示相同的可能性集。叶子节点是单例 （singletons）;每一个代表一个可行的解决方案。注意，该算法是精确的。它提供了与单纯方法相同的解决方案，只要内部节点c的得分©是其元素得分的上界。在这种情况下，无论什么时候一个节点是有界的，这个子树中都不存在一个比目前已知的最好的解更好的解。 —-Cartographer_Google的论文

分支定界法讲解

深度优先搜索

• 对于一颗二叉树来说，形似如下图形式的顺序依次访问每个节点的搜索方式叫做DFS，深度优先搜索。

• 

认识整数规划

先了解线性规划

• 线性规划(Linear Programming 简记 LP)是了运筹学中数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出 求解线性规划的单纯形法以来，线性规划在理论上趋向成熟，在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划现代管理中经常采用的基本方法之一。 在解决实际问题时，需要把问题归结成一个线性规划数学模型，关键及难点在于选适当的决策变量建立恰当的模型，这直接影响到问题的求解。

• 线性规划问题的目标函数及约束条件均为线性函数；约束条件记为 s.t.(即 subject to)。目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以 是小于号也可以是大于号。

• 一般线性规划问题的数学标准型为

  $$\begin{array}{r}maxz=\sum _{j=1}^n{c}_j{x}_j\end{array}\text{\hspace{1em}(3)}$$

  $$\begin{array}{r}s.t.\{\begin{array}{l}{\sum }_{j=1}^n{a}_{ij}{x}_j=b_{i}i=1,2,...,m\\ x_j\ge 0j=1,2,...,n\end{array}\end{array}\text{\hspace{1em}(4)}$$

• 例题

  某机床厂生产甲、乙两种机床，每台销售后的利润分别为4000元与3000元。生产甲机床需用A、B机器加工，加工时间分别为每台2小时和1小时；生产乙机床需用A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？

  机床	利润	加工机器&工时(\h)
  甲	4000元	A (2)、B (1)
  乙	3000元	[A (1)、B (1)、C (1)]

  上述问题的数学模型：

  设该厂生产$x_1$$ 台甲机床和 $$x_2$$乙机床时总利润最大，则$$x_1$$,$$x_2$应满足

  $$\begin{array}{r}(目标函数)maxz=4x_1+3x_2\end{array}\text{\hspace{1em}(1)}$$

  $$\begin{array}{r}s.t.(约束条件)\{\begin{array}{l}2x_1+x_2\le 10\\ x_1+x_2\le 8\\ x_2\le 7\\ x_1,x_2\ge 0\end{array}\end{array}\text{\hspace{1em}(2)}$$

• 上述例题中变量$$x_1,x_2$$称之为决策变量，(1)式被称为问题的目标函数，(2)中的几个不等式是问题的约束条件，记为s.t.(即subject to)。由于上面的目标函数及约束条件为线性函数，故被称为线性规划问题。

线性规划问题的解的概念

• 可行解：满足4个约束条件的解，称为可行解。 而使目标函数达到最大值的可行解叫最优解。
• 可行域：所有可行解构成的集合称为问题的可行域，记为R 。

求线性规划解的方法

• 图解法（高中常用方法）

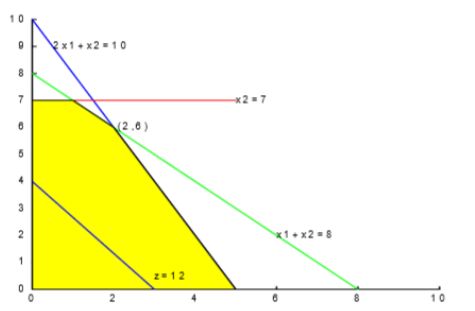
  简单直观，适用于二维决策变量，它有助于了解线性规划问题求解的基本原理。。对于每一固定的值z，使目标函数值等于z的点构成的直线称为目标函数等位线，当z变动时，我们得到一族平行直线。

  

  图解法简单直观,对于每一固定的值z，使目标函数值等于z的点构成的直线称为目标函数等位线，当z变动时，我们得到一族平行直线。等位线向上平移即可找到事目标函数有最大值的点。不难看出最优解为(2,6)，带入目标函数即可。

• 单纯形法（计算机常用方法）

  当变量变多时，我们不能简单的画出图像，并且为了能够让计算机计算，我们需要借助单纯形法。单纯形法是求解线性规划问题最常用、最有效的算法之一。

  线性规划之单纯形法描述

  这个算法的思想可以用几何术语描述如下：

  先在可行域中找到一个极点，然后检查一下是不是在邻接极点除可以让目标函数取值更佳。如果不是，当前顶点就是最优点，然后算法停止；如果是，转而处理那个能让目标函数取值更佳的邻接顶点。有限步以后，该算法要么发现了一个取到最优解的极点，要么证明了最优解不存在。

  参考《算法设计与分析基础》潘彦译 P267

整数规划的分类

• 如不加特殊说明，一般指整数线性规划。对于整数线性规划模型大致可分为两类：

  • 变量全限制为整数时，称纯（完全）整数规划。
  • 变量部分限制为整数的，称混合整数规划。

整数规划特点

• 原线性规划有优解，当自变量限制为整数后，其整数规划解出现下述情况：

  • 原线性规划优解全是整数，则整数规划优解与线性规划优解一致。
  • 整数规划无可行解。
  • 有可行解（当然就存在优解），但优解值变差。

• 整数规划优解不能按照实数优解简单取整而获得。

• 例题1

  原线性规划为：

  $$\begin{array}{rl}& minz=x_1+x_2\\ & 2x_1+4x_2=5,x_1\ge 0,x_2\ge 0\end{array}$$

  $$\begin{array}{r}其最优实数解为:x_1=0,x_2=\frac{5}{4},minz=\frac{5}{4}\end{array}$$

• 例题2

  原线性规划为：

  $$\begin{array}{rl}& minz=x_1+x_2\\ & 2x_1+4x_2=6,x_1\ge 0,x_2\ge 0\end{array}$$

  $$\begin{array}{r}其最优实数解为:x_1=0,x_2=\frac{3}{2},minz=\frac{3}{2}\end{array}$$

  $$\begin{array}{r}若限制整数得:x_1=1,x_2=1,minz=2\end{array}$$

整数规划如何求解

• 分枝定界法—可求纯或混合整数线性规划。
• 割平面法—可求纯或混合整数线性规划。
• 隐枚举法—求解“0-1”整数规划：
  • 过滤隐枚举法
  • 分枝隐枚举法
• 匈牙利法—解决指派问题（“0-1”规划特殊情形）
• 蒙特卡洛法—求解各种类型规划

分枝定界法

分枝定界是一种深度优先的树搜索算法。通过对树进行剪枝，可以缩小了搜索范围，大大减小计算量。但同时又不会遗漏最优解。请现在就记住，分枝定界思想，就是不断缩小搜索范围的过程。

主要思路

• 对有约束条件的优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分枝与定界内容。

• 通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。这就是分枝定界法的主要思路。

• 分枝定界法可用于解纯整数或混合的整数规划问题。在本世纪六十年代初由 Land Doig 和 Dakin 等人提出的。由于这方法灵活且便于用计算机求解，所以现在它已是解整数规划的重要方法。目前已成功地应用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。

举例分析

​ 设有最大化的整数规划问题$A$，与它相应的线性规划为问题$B$，从解问题$B$开始，若其最优解不符合$A$的整数条件，那么$B$的最优目标函数必是$A$的最优目标函$z^{\ast }$的上界,记作$\overline{z}$；

而$A$的任意可行解的目标函数值将是$z^{\ast }$的一个下界 $\underline{z}$。

分支定界法就是将$B$的可行域分成子区域的方法。逐步减小$\overline{z}$和增大$\underline{z}$，最终求到$z^{\ast }$。

• 例

  $$Maxz=40x_1+90x_2$$

  $$\begin{array}{r}s.t.\{\begin{array}{l}9x_1+7x_2\le 56\\ 7x_1+20x_2\le 70\\ x_1,x_2\ge 0,且为整数\end{array}\end{array}$$

  解：

  • 先不考虑整数限制，即解相应的线性规划$B$，得最优解为：

    $$x_1=4.8092,x_2=1.8168,z=355.8779$$

    可见她不符合整数条件。这时$z$是问题$A$ 的最优目标函数值$z^{\ast }$的上界，记作$\overline{z}$。而$x_1=0，x_2=0$显然是问题A的一个整数可行解，这时$z=0$,是$z^{\ast }$的一个下界，记作$\underline{z}$,即$ 0\le z^* \le 355$。

  • 因为$x_1,x_2$当前均为非整数，故不满足整数要求，任选一个进行分枝。设选$x_1$进行分枝，把可行集分成2个子集(以下为增加的约束)：

    $$x_1\le [4.8092]=4,x_1\ge [4.8092]+1=5$$

    因为4与5之间无整数，故这两个子集的整数解必与原可行集合整数解一致。这一步称为分枝。这两个子集的规划及求解如下：

    • 问题$B_1:$

      $$Maxz=40x_1+90x_2$$

      $$\begin{array}{r}\{\begin{array}{l}9x_1+7x_2\le 56\\ 7x_1+20x_2\le 70\\ 0\le x_1\le 4,x_2\ge 0\end{array}\end{array}$$

      $$最优解为:x_1=4.0,x_2=2.1,z_1=349$$

    • 问题$B_2:$

      $$Maxz=40x_1+90x_2$$

      $$\begin{array}{r}\{\begin{array}{l}9x_1+7x_2\le 56\\ 7x_1+20x_2\le 70\\ x_1\ge 5,x_2\ge 0\end{array}\end{array}$$

      $$最优解为:x_1=5.0,x_2=1.57,z_1=341.4$$

    • 再定界：$0\le z^{\ast }\le 349$

  • 对问题$B_1:$再对不是整数的$x_2$进行分枝得问题$B_{11}$和$B_{12}$，它们的最优解为：

    • $B_{11}:x_1=4,x_2=2,z_{11}=340$

    • $B_{12}:x_1=1.43,x_2=3.00,z_{12}=327.14$

    • 由开头所说，线性规划$B$的最优目标函数值必是$A$的最优目标函数$z^{\ast }$的上界,记作$\overline{z}$，整数规划$A$的任意可行解的目标函数值将是$z^{\ast }$的一个下界$\underline{z}$。

    • 再定界有：$340\le z^{\ast }\le 349$，并将不在这个范围内的$B_{12}$剪枝。

  • 对问题$B_2$再进行分枝得问题$B_{21}$和$B_{22}$，它们的最优解为：

    • $B_{21}:x_1=5.44,x_2=1.00,z_{22}=308$
    • $B_{22}无可行解$
    • 再定界有：$340\le z^{\ast }\le 341$,将$B_{21},B_{22}$ 剪枝。

  • 于是可以断定原问题的最优解为：

    $$x_1=4,x_2=2,z^{\ast }=340$$

  • 但是我认为现在还不能断定这个解就是原问题的最优解，刚开始是选择的是x1,我认为可能还需要对x2进行这样的分枝定界才能最终确定最优解是什么，可能理解的不准确仅作参考。

• 图解如下

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kfAGMBdf-1658380611043)(https://s2.loli.net/2022/03/11/g3ybaIxYeNlLqSA.png)]

• 这部分只能把抽象的方法讲清楚，具体的代码实现和数学计算细节请参考论文Cartographer_Google的论文，我全文翻译的看过一遍，但是还有很多细节概念不理解，为了不误人子弟就暂不深究。

实际应用

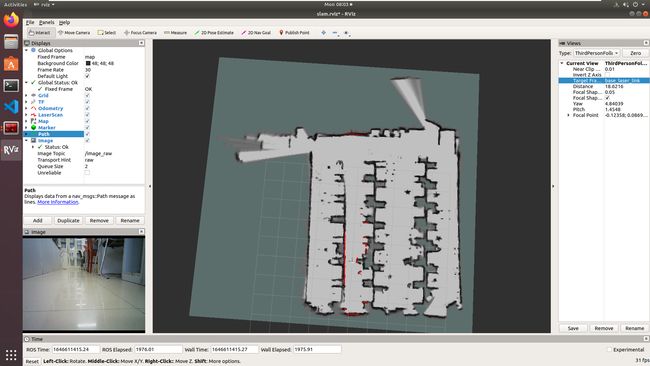
室内建图

室内导航避障

上传到b站视频：https://www.bilibili.com/video/BV1U3411W7AK/

错误修订

• 将原来B2的子问题B11改为B21
• 二叉树部分，原来写的头节点改为根节点