图示时序卷积网络(Temporal Convolutional Networks)结构与过程
参考:
Temporal Convolutional Networks and Forecasting - Unit8 翻译原意为主, 加入部分补充说明
Darts: unit8co/darts: A python library for easy manipulation and forecasting of time series. (github.com)
Darts-TCN 例子: darts/05-TCN-examples.ipynb at master · unit8co/darts (github.com)
TCN论文: 《An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling》
卷积网络(Convolutional Neural Network, CNN)过去广泛应用于图像领域, 最近有工作发现, 经过改造的 CNN 可以高效完成序列(sequence)建模与预测. 本文详细说明了时序卷积网络(Temporal Convolutional Network, TCN)中的基本块(block)结构, 并且借助开源时间序列预测库 Darts, 用 TCN 实现在真实数据集上的准确预测.
下面对 TCN 的相关描述参考了文献《An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling》, 具体参考位置以[*]标出.
Motivation
长期以来, 深度学习领域通常采用循环神经网络(Recurrent Neural Network, RNN)完成序列建模任务, 比如 LSTM 和 GRU. 然而, [*]指出 CNN 在序列建模上潜力巨大, 并且在许多任务上表现甚至超过 RNN, 同时避免了 RNN 的共性问题, 比如梯度爆炸/消失、长期记忆差; 并且CNN 支持并行计算, 因此效率高于 RNN. 下面将详细介绍 [*] 提出的 TCN 结构, 文中参数命名与 Darts 实现保持一致, 以粗体表示.
模型基本原理
TCN 有以下 4 个关键特性:
- 一维卷积(1DConv)
- 卷积层输入输出 length 相同
- 因果(causal)卷积
- 膨胀(dilated)卷积
译者注:
- 本文中 length 表示时间序列的长度, size 表示每个时刻的特征数. 特征维度 size 对应 channel, 卷积操作发生在 length 维度上.
- 下文中会出现两类 length, 一是指 TCN 网络的输入输出 length, 二者是相等的, 不加粗; 二是指数据的 input_length 和 output_length, 可以不相等, 加粗.
1DConv 一维卷积
一维卷积的输入输出都是三维 tensor, TCN 中, 输入 shape 为 (batch_size, input_length, input_size), 输出 shape 为 (batch_size, input_length, output_size).
TCN 每一层的输入和输出 length 相同, 只有第三维(size)不同, 单变量场景(一元时间序列)下, input_size 和 output_size 都是 1. 更一般的多元问题中, 二者可以大于 1, 并且 input_size 和 output_size 可以不相等, 比如输入为多元, 目标输出只有一元.
例一: input_size == output_size == 1
下面首先说明最简单的情形, 即 batch_size、input_size、output_size 都等于 1, 卷积核大小(kernel_size)为 3.

如图, 卷积操作中, 一个输出元素, 对应连续的 kernel_size 长的输入元素. 计算方式是与 kernel_size 长的 kernel 向量做点积. 计算下一个输出元时, 卷积核向右"滑动"一位(这里滑动一位即卷积层设置 stride=1, 是预测任务中的普遍设置). 注意, 计算时, 卷积核不断移动, 但是卷积核权重保持不变, 每个输出元素都是由相同的权重计算而来. 下图展示了连续两个输出元素对应的输入子序列:

注意: 为了简洁表示, 这里没有展示 kernel 的点积操作, 只需记住所有 input 到 output 的卷积计算中, 都需要这样的点积操作. 下文同理.
例二: input_size == 2
当 size > 1 时, 对应 CNN 层的多个 channel, 上述过程对每个 channel 执行, 但不同 channel 的 kernel 权重不同. 如下图所示:
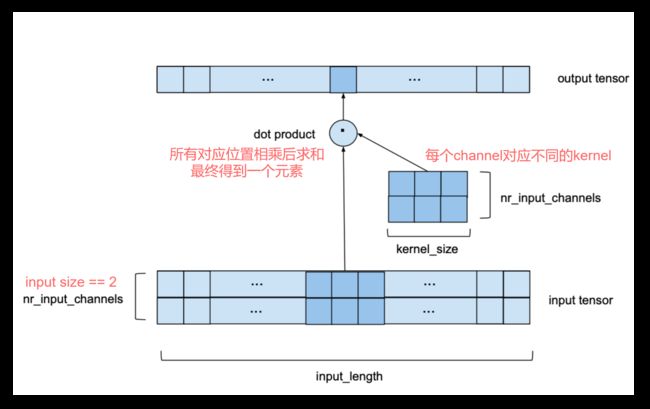 可以发现, 该过程体现出二维卷积的特点, 可以看做输入 tensor 的 shape 为(input_length, input_channel) (注:原文中写的是 size*channel, 应为笔误), 卷积核 shape 为(kernel_size, input_channel)的 2DConv. 但其本质依然是 1DConv, 因为固定了卷积核的宽度为 input_channel, 所以 kernel 只沿着 length 维度移动.
可以发现, 该过程体现出二维卷积的特点, 可以看做输入 tensor 的 shape 为(input_length, input_channel) (注:原文中写的是 size*channel, 应为笔误), 卷积核 shape 为(kernel_size, input_channel)的 2DConv. 但其本质依然是 1DConv, 因为固定了卷积核的宽度为 input_channel, 所以 kernel 只沿着 length 维度移动.
同样, 如果 output_channel 也大于 1, 那么对每一个 outpu_channel 也做上述操作, 并且 kernel 的权重不同. 此时, 总权重数目为 kernel_size * input_channel * output_channel.
channel 的取值与对应层的位置有关, 输入层的 input_channel = input_size, 输出层 output_channel = output_size. Darts 中其他位置的 channel 数都为 num_filters.
输入输出 length 相等
由上面的例子可以看出, 卷积计算下, 输出 tensor 的 length 与输入 tensor 往往不相等(kernel_size>1 时, 输出 length 小于输入 length). 为了保证相等, 则需要对输入 tensor 补零(zero-padding), 即在 length 维度上向左右两侧补充 0 元素, 由此调节输出 tensor 的 length. TCN 中的补零方式将在下一节(因果卷积)中说明.
因果卷积
所谓因果, 即序列中任意位置 i 上的元素只受它之前的元素影响, 而不受后面元素的影响. 换言之, 预测位置 i 的元素, 应当仅用 i 之前观察到的元素, 而不能用未来的观察. 这样就对补零方式提出了要求.
传统图像处理中, 往往在四周对称补零, 而在因果卷积中, 只在输入 tensor 的 length 维度左侧补零.
不难理解, 要满足"因果"的要求, 输出 tensor 的首元素只能参考输入 tensor 的首元素, 这样不足 kernel_size 的部分必须用 0 补全; 而 output tensor 的尾元素也不能参考未来的元素, 所以 input tensor 的右侧补零没有意义. 如下图所示:
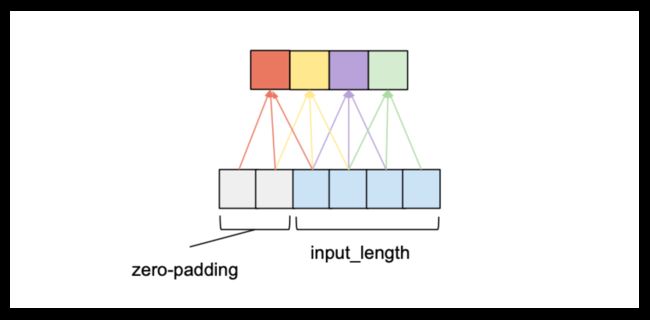
这里 input_length=4, kernel_size=3, 需要在左侧补足 kernel_size 的大小, 才能得到首元素(红色方格).
在没有膨胀卷积时, 补零的数目为 kernel_size - 1.
膨胀卷积
感受域
首先说明感受域(receptive field)的概念: 感受域表示一个输出元素受到多少输入元素的影响, 由卷积网络结构决定. 如下图所示, 2 层 kernel_size = 3 的卷积网络, 感受域大小为 5.

推广到一般情形: kernel 长为 k 的 n 层卷积层, 感受域为: r = 1 + n × ( k − 1 ) r = 1 + n\times(k-1) r=1+n×(k−1)
为什么需要膨胀卷积
序列预测任务中, 我们希望感受域尽可能大, 最好能够覆盖整个 input_length, 这样就能够利用已知的全部信息进行预测, 文中称为 full history coverage.
普通卷积下, 根据公式, 假设 input_length = l l l, 需要的卷积层数为: n = ⌈ ( l − 1 ) / ( k − 1 ) ⌉ n = \lceil (l-1) / (k-1) \rceil n=⌈(l−1)/(k−1)⌉, 与 l l l 是线性关系.
当 l l l 比较大时, 就需要很多层卷积网络, 需要学习的权重参数过多, 并且过深的网络存在退化问题, 不利于训练.
引入膨胀卷积就是为了提高感受域的增加速率, 以降低网络层数.
什么是膨胀卷积
上文所述的普通卷积网络作用于输入 tensor 的连续元素, 而膨胀卷积中, 卷积核对应的输入元素间有间隔. dilation 的值就是间隔大小, 默认情况下 dilation=1, 下图展示了 dilation=2 的情景, 这里 kernel_size=3, input_length=4.

可以看到, 参与卷积的输入元素下标间距为 2. 相比普通卷积, 同样的卷积核大小, 得到感受域为 5. 此时感受域变为: r = 1 + n × d × ( k − 1 ) r = 1+n\times d\times (k-1) r=1+n×d×(k−1), 获得常数级提升. 此处以 d 表示 dilation 值.
进一步, 令 d 随 n (网络深度)指数级增加, 取 dilation_base 记为 b, 在第 i 层, d = b i d = b^i d=bi, 下图给出一个例子. 其中 input_length = 10, kernel_size=3, dilation_base = 2, 三层卷积网络即实现完全覆盖.
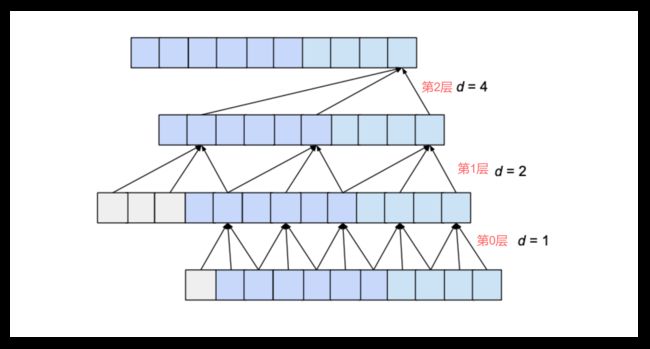
这里只展示了输出 tensor 的末尾元素计算以及对应的补零位置, 实际上, 上面的网络结构最多支持 length=15 的全覆盖.
如此, n 层 TCN 网络的感受域长度 w 为:
w = 1 + ∑ i = 0 n − 1 ( k − 1 ) × b i = 1 + ( k − 1 ) × b n − 1 b − 1 w=1+\sum_{i=0}^{n-1}(k-1)\times b^i = 1+(k-1)\times \frac{b^n-1}{b-1} w=1+i=0∑n−1(k−1)×bi=1+(k−1)×b−1bn−1
此处 k 为 kernel_size, b 为 dilation_base.
注意, 不合适的 k 和 b 可能导致空洞, 比如, 若 b=3, k=2:
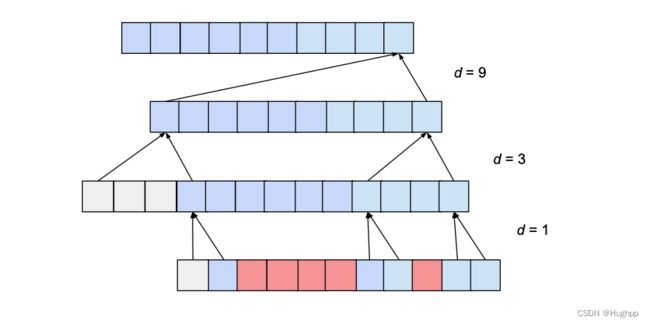
虽然长度上满足要求, 但是红色方格的元素并没有被覆盖到, 这样的设置是不合理的. 需要将 k 增大到 3 , 或 b 减小到 2. 一般地, 要实现无空洞的全覆盖, 应保证 b ≤ k b \le k b≤k.
因此, 要实现对 length = l l l 的全覆盖, 层数 n :
n = ⌈ l o g b ( ( l − 1 ) ( b − 1 ) ( k − 1 ) + 1 ) ⌉ n = \left\lceil log_b\left( \frac{(l-1)(b-1)}{(k-1)} +1 \right) \right\rceil n=⌈logb((k−1)(l−1)(b−1)+1)⌉
这样一来, 网络层数由线性增长减低到指数增长.
补零个数
限制 input_length 每层都相等的情况下, 第 i 层补零个数 p 为: $p = b^i \times (k-1) $
解释: 因为每层实际的有效 length 都为 input_length, 补 0 的个数即为卷积核总跨度-1(总跨度由 k 和 d 决定, 应去掉首元素占一个位置).
TCN 全貌
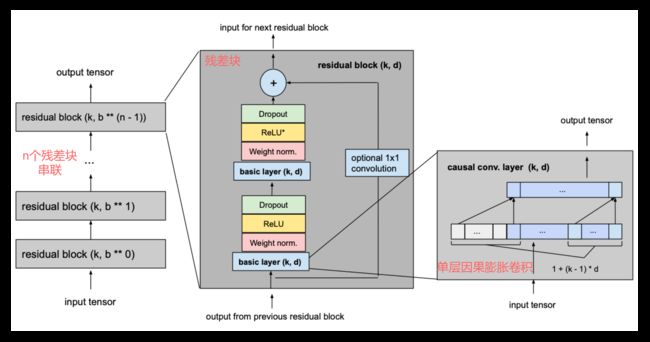
整合上述设计, TCN 整体结构如下:
训练与预测
在时间序列预测任务中, 通过已知序列预测未来的序列, 通常原始数据集较长, 训练时输入一段连续的子序列.
TCN 的输出输出 length 相等, 因此网络输出的序列长度与 input_length 相等.
根据预测需要, 具体向后预测的步数(即 output_length)不超过 input_length 即可(向后预测的长度也称为 forecasting horizon), 允许输入输出序列出现部分重叠. 如下图所示:
模型其他改进
[*]以上述 TCN 为基础, 添加了一些深度学习常用的改进设计, 包括残差连接(residual connection)、正则化(regularization)、激活函数(activation function).
残差块(residual block)
残差是将网络输出与原始输入相加作为最终输出结果, 是常用的深度学习优化技巧.
残差块构造是对基础模型的最大改变. 将原有 TCN 中的各层因果膨胀卷积层替换成为一个残差块, 块内是两层 dilation 相同的 1DConv 层, 并添加残差连接, 如下图所示.

这里残差连接的 1*1 卷积起到变换输入 channel 数的作用, 保证与网络输出的 channel 一致, 才能相加.
Darts 中, 除输入层和输出层的 channel 有变化, 中间各层的输入输出 channel 相等, 由 num_filters 指定. 而输出层输出层涉及到 channel 的调整, 残差连接中需要用到 1*1 卷积.
这一步的改进中, 增加了一层膨胀卷积, 因此感受域也变长了, 第 n 块的感受域长度 w , 和全覆盖要求的残差块个数 n 计算公式更新为:
w = 1 + ∑ i = 0 n − 1 2 ⋅ ( k − 1 ) ⋅ b i = 1 + 2 ⋅ ( k − 1 ) ⋅ b n − 1 b − 1 n = ⌈ l o g b ( ( l − 1 ) ( b − 1 ) ( k − 1 ) ⋅ 2 + 1 ) ⌉ w=1+\sum_{i=0}^{n-1}2\cdot(k-1)\cdot b^i = 1+2\cdot (k-1)\cdot \frac{b^n-1}{b-1} \\ n = \left\lceil log_b\left( \frac{(l-1)(b-1)}{(k-1) \cdot 2} +1 \right) \right\rceil w=1+i=0∑n−12⋅(k−1)⋅bi=1+2⋅(k−1)⋅b−1bn−1n=⌈logb((k−1)⋅2(l−1)(b−1)+1)⌉
激活函数, 归一化(normalization)和正则化
使用 ReLU 作为激活函数.
为避免梯度爆炸问题, 加入 weight normalization 层.
为避免过拟合, 加入 dropout 层引入正则化.
最终一个残差块结构如下:

第二层 ReLU 的星号表示最后一个输出层不加激活函数, 以支持负数输出(这与[*]中的设计不同).
最终版 TCN
这里, l l l 为输入子序列长度 input_length; k k k 为卷积核大小 kernel_size; b b b 为膨胀底数 dilation_base, 且保证 b ≤ k b\le k b≤k ; n n n 为残差块总数, 由完全覆盖公式计算得到.
Darts 用例
下面介绍使用 Darts 库 TCN 预测时间序列的流程.
准备数据集
这里用到 Kaggle dataset, 使用西班牙的每小时发电量数据, 预测"run-of-river hydroelectricity(川流式水力发电)"的值, 为了缩小问题规模, 将每天的发电量取均值得到粒度为"天"的序列.
from darts import TimeSeries
from darts.dataprocessing.transformers import MissingValuesFiller
import pandas as pd
df = pd.read_csv('energy_dataset.csv', delimiter=",")
df['time'] = pd.to_datetime(df['time'], utc=True)
df['time']= df.time.dt.tz_localize(None)
df_day_avg = df.groupby(df['time'].astype(str).str.split(" ").str[0]).mean().reset_index()
value_filler = MissingValuesFiller()
series = value_filler.transform(TimeSeries.from_dataframe(df_day_avg, 'time', ['generation hydro run-of-river and poundage']))
series.plot()
序列可视化:
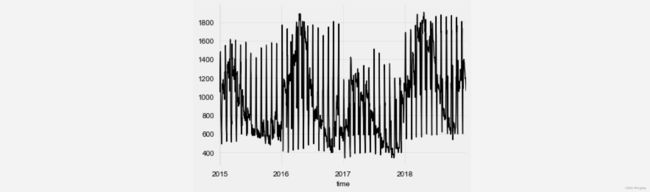
可以看到, 数据有每年的季节性变化, 还出现有规律的峰值(大约以月为间隔), 因此, 最好在全局日期之外, 加入"current day of the month(每月几号)"作为额外特征, 有利于快速收敛. 这样输入通道数(input_size)为 2.
series = series.add_datetime_attribute('day', one_hot=True)
最后, 将数据集划分为训练集和验证集, 并标准化(standardization).
from darts.dataprocessing.transformers import Scaler
train, val = series.split_after(pd.Timestamp('20170901'))
scaler = Scaler()
train_transformed = scaler.fit_transform(train)
val_transformed = scaler.transform(val)
series_transformed = scaler.transform(series)
模型创建与训练
设置 output_length = 7 表示每次预测一周.
训练和验证时, 目标序列关注电量, 不带处理数据集时额外加入的"每月几号"参数.
from darts.models import TCNModel
model = TCNModel(
input_size=train.width,
n_epochs=20,
input_length=365,
output_length=7,
dropout=0,
dilation_base=2,
weight_norm=True,
kernel_size=7,
num_filters=4,
random_state=0
)
model.fit(
training_series=train_transformed,
target_series=train_transformed['0'],
val_training_series=val_transformed,
val_target_series=val_transformed['0'],
verbose=True
)
模型评估
这里想使用训练好的模型, 在验证集的不同时间点上做测试, 这里使用了 backtest 函数, 并将 stride 设置为 5 以节约时间.
测试时输入的数据与训练不同, 但不再更新模型参数.
pred_series = model.backtest(
series_transformed,
target_series=series_transformed['0'],
start=pd.Timestamp('20170901'),
forecast_horizon=7,
stride=5,
retrain=False,
verbose=True,
use_full_output_length=True
)
最后将测试结果与真实值对比, 并可视化:
from darts.metrics import r2_score
import matplotlib.pyplot as plt
series_transformed[900:]['0'].plot(label='actual')
pred_series.plot(label=('historic 7 day forecasts'))
r2_score_value = r2_score(series_transformed['0'], pred_series)
plt.title('R2:' + str(r2_score_value))
plt.legend()
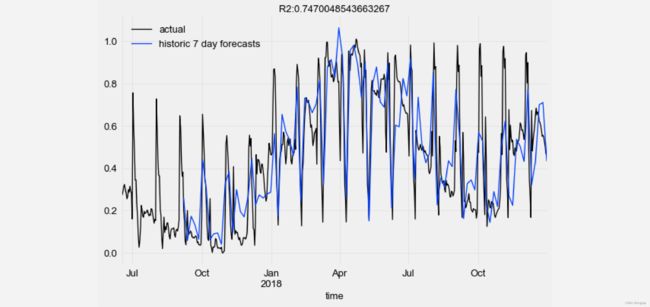
更多相关细节, 可参考 darts/05-TCN-examples.ipynb at master · unit8co/darts (github.com)