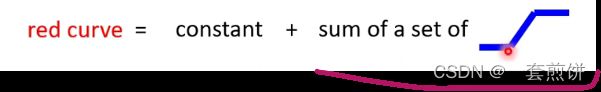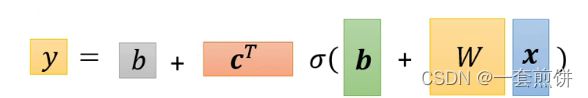李宏毅2021/2022春机器学习-深度学习的基本概念（2）
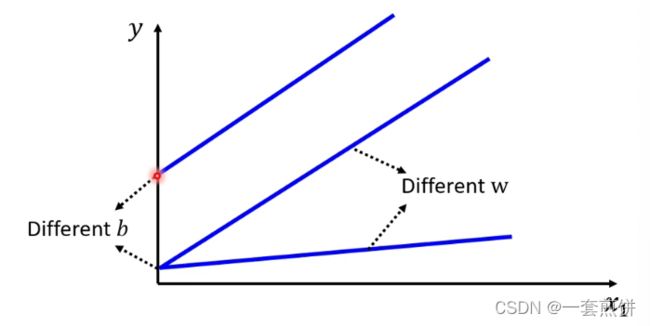
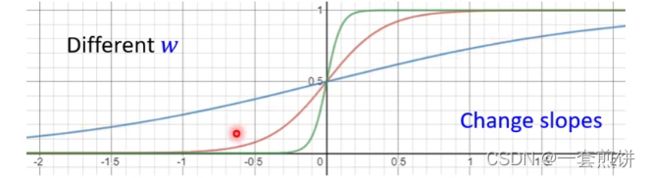
Linear model 是太过简单的，x1和y的关系：可以用一条带有斜率的直线表示，随着x1的增大，y 也会逐渐增大。可以设定不同的w 来改变斜线的斜率，可以设定不同的b来改变斜线的与y轴的交叉点。，但是无论怎么改变w和b 他都是一条直线。并且是y随着x1的改变而发生变化。
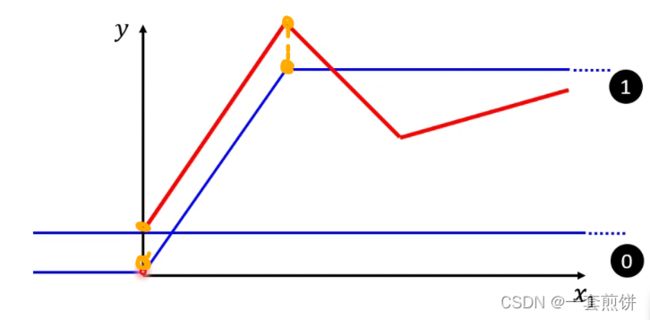
如图所示：
(前一天观看的人数越多，隔天的人数也就越多)
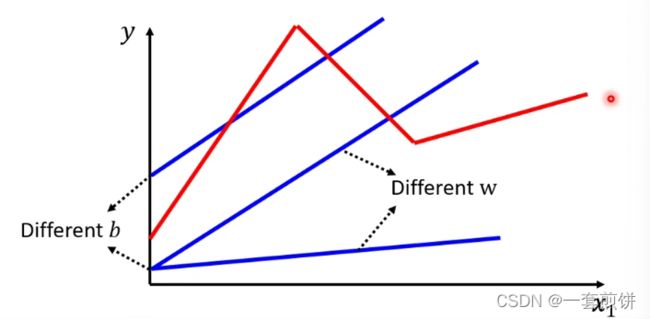
但是，现实的阅读量可能并不是如上图当中所显示的。
（阅读量会出现红色线所表示的这样），无论怎么改变w和b都无法出现红色线，没办法用Linear model 制造出红色线。所以Linear model有很大的限制，叫做model bias。
model bias：没办法模拟真实的情况，在这种情况我们就要书写一个更有弹性，更复杂，有未知的函数。
那如何写这个函数呢？
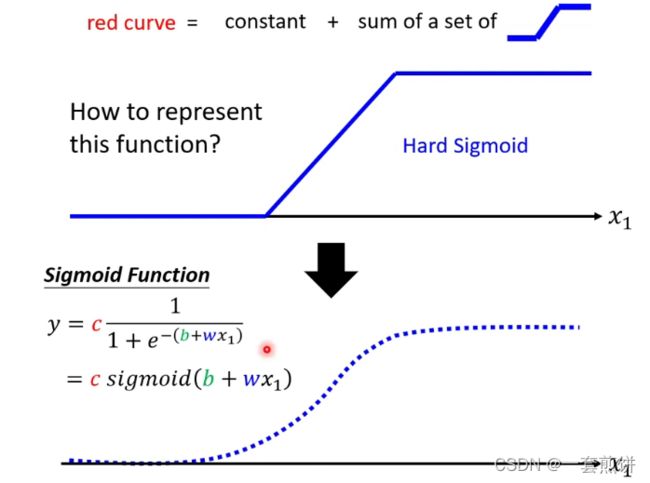
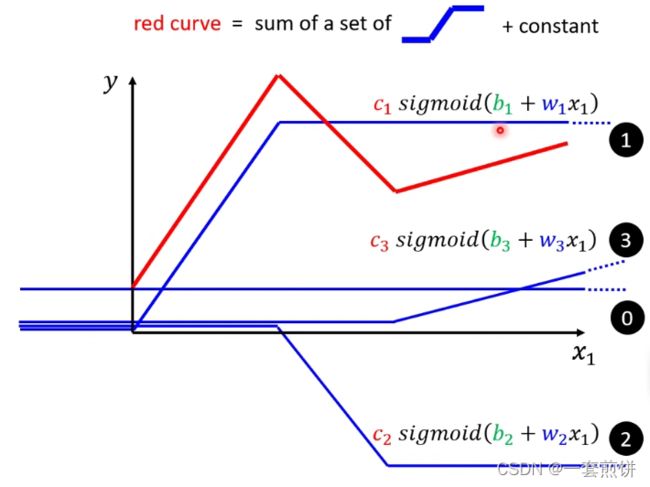
可以观察到红色线的函数时一个常数加上一个固定的函数，那这个固定的函数就是形如下图的函数
那这常数项的值是有多大呢？就是看红色线与x轴的交点在哪里，那常数项就跟x轴的交点一样大。
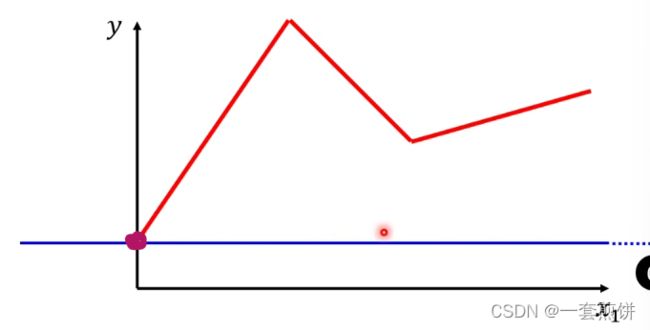
那怎么知道常数项加上蓝色的函数就是红色线呢？
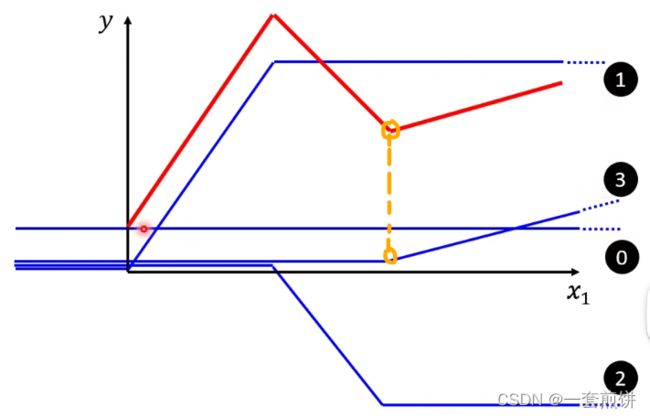
（1）蓝色线斜坡的起点设在红色线的起点的地方，胁迫的终点也是红色线的拐点处，并且蓝色线的斜坡的斜率和红色线的斜率一样。0线+1线就是红色线转折之前的部分。（得到的就是红线起点到第一个转折点之间的线）
（2）再加第二个蓝色线（第二个函数）：看红色线的第二个转折点出现在哪里，所以这条蓝色的线得斜坡就在红线函数的第一个转折点到第二个转折点之间。0线+1线+2线就得到红色线。（得到的时红线第一个转折点与第二个转折点之间的线）
（3）第二个转折点之后的部分怎么产生的呢？加上第三个蓝色的线（
）第二个转折点与蓝色线的转折点一样。斜率也是一样的，所以0线+1线+2线+3先后就得到红色的线
Piecewise Linear Curves
形如红色线的就叫做Piecewise Linear Curves，都是一个常数加上一堆的蓝色线，红色线的形状越复杂，蓝色的线就越多。
如果不是Piecewise Linear Curves （锯齿状的线）
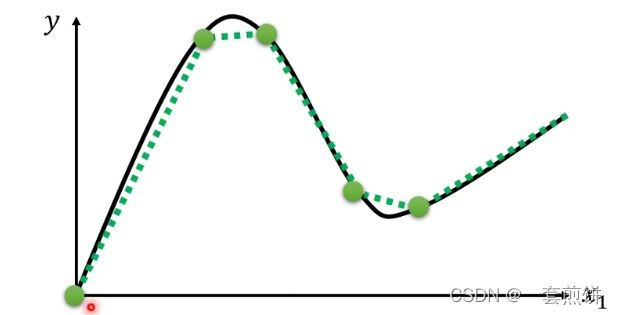
如果是曲线的话：可以现在曲线上取一些点，再把这些点用直线连接起来，变成Piecewise Linear Curves。如图所示：
（连接起来的线与原来的曲线非常的接近）
所以通过上面的这个例子我们知道可以用Piecewise Linear Curves去逼近任意一条曲线，然后用一堆蓝色的线组合起来。
蓝色线的函数应该如何表示呢？（可以用一条曲线去逼近）
假设输入的x1的值时无穷大的时候，指数部分就会消失，曲线就会收敛到c的部分，变成常数c.
假设输入的x1的值是负无穷大的时候，y的值就趋近于0。
如何制造出合适的Hard sigmoid呢？和w，b，c有关。
举例：
（1）
改变w，就会改变S线的斜破的斜度。
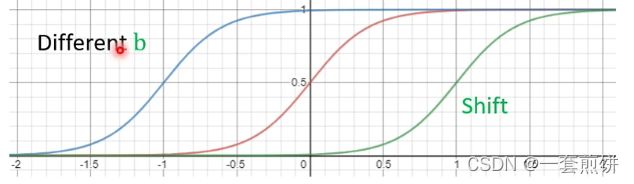
（2）
改变b，会发生S 线的左右移动。
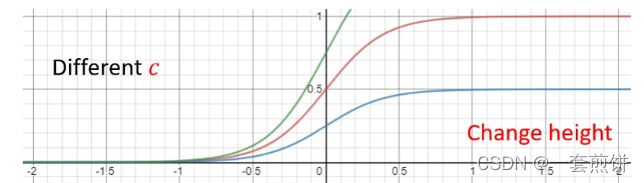
（3）
改变c，会改变S 线的高度。
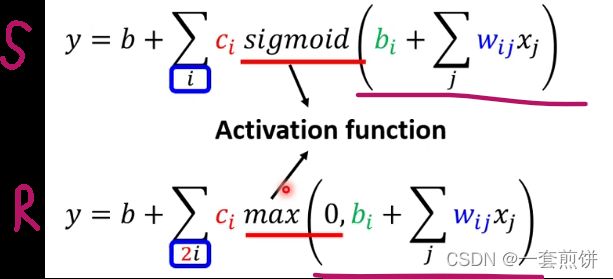
总结来说：上面的过程就是红色线的函数表达式的建立，就是常数加上多个Sigmoid。S线的形状是由w,b,c有关。
把下图中的0，1，2，3线加起来得到的表达式： 
第一个函数对新的模型又很多的bias，所以我们建立了第二个函数（更具弹性），同理，也可以根据上图中的第三个函数建立第四个函数，形式式一样的。
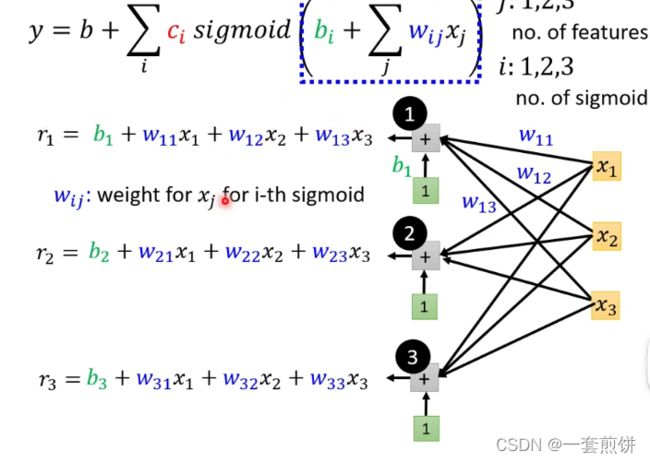
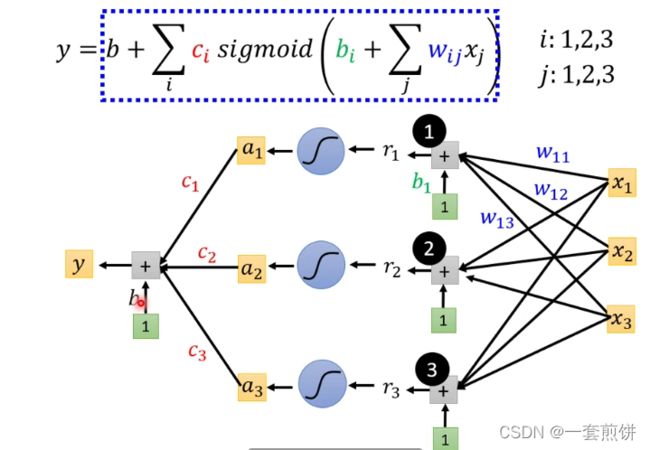
现在解释一下第四个函数表达式：（分解步骤）
在这个式子当中j表示的是 天数，前一天，前两天，前三天。
输入就是x1 ,x2 ,x3 前一天观看的人数，前两天观看的人数，前三天观看的人数。
i：每一个i就代表一个蓝色的函数
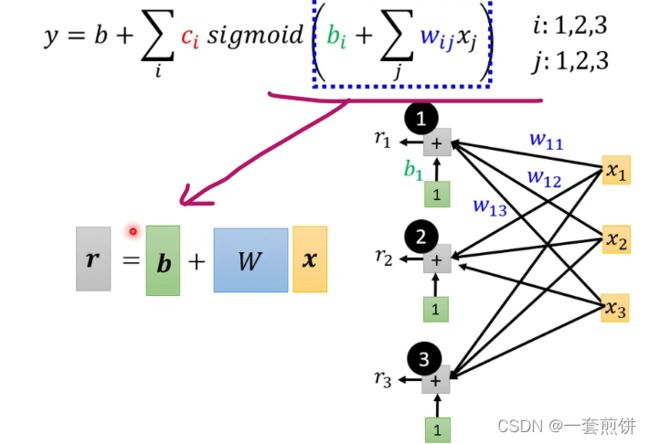
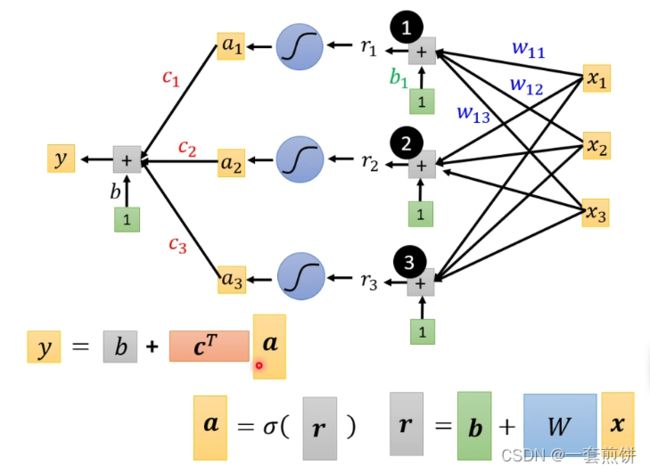
我们可以将上面的式子做一个矩阵的简化：
所以括号里面的式子就可以表示成：
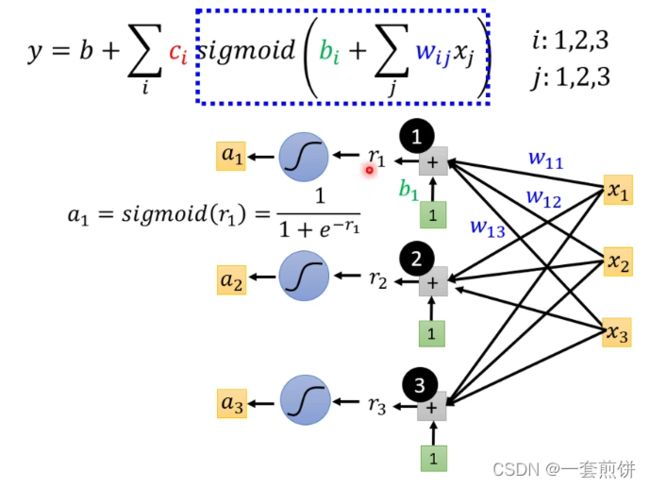
接下来r1,r2,r3通过不同的Sigmoid Function :
两个式子可以相互表示：
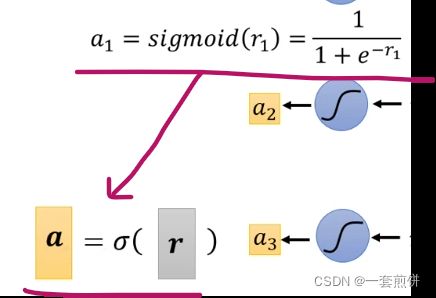
最后的步骤是：
如果上面的步骤用矩阵的形式表示的话：
这三个式子整体相结合：
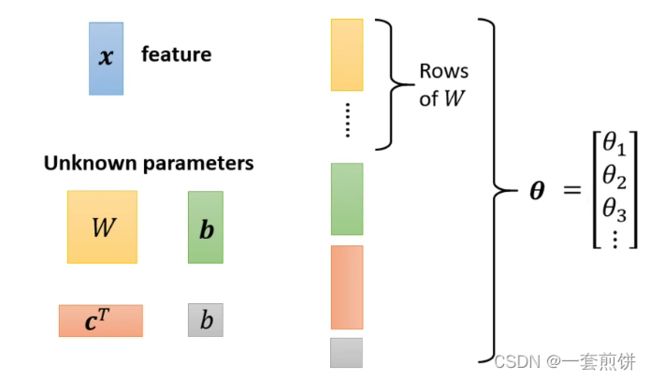
再讲怎么找出位置的参数之前，稍微讲一下重新定义一下我们的符号：
把四个未知参数中的元素按照行或者列的形式展开，形成一个新的矩阵
，如上图所示，也就是所 有的未知参数统称为
上面的部分已经完成了新函数的第一步。
问题：式子当中的Sigmoid的个数是自己决定的，并不止三个，Sigmoid越多，函数就越复杂，九月逼近于Hard sigmoid.
接下来进行第二步：
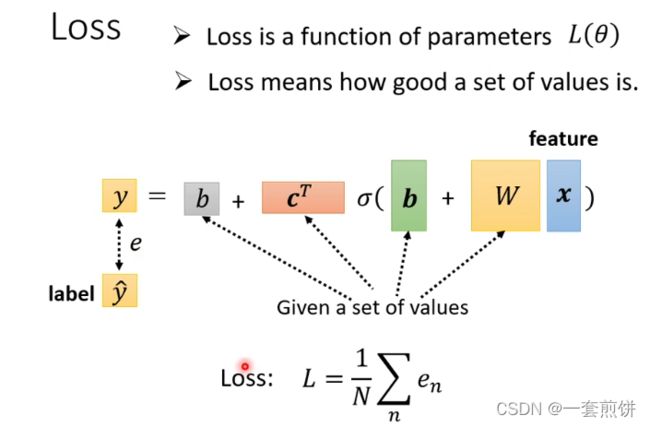
LOSS:功能还是没有发生改变，但是表示的形式发生了改变。L()
计算的方法跟两个参数的的时候的方法是一样的，先给定某一组w，b，cT和b的值带入到函数当中去，然后再将向量x带入到函数中得到y的值（估测的值），在计算一下和真实的Label之间的差距。得到误差是e，在把所有的误差e相加起来，就得到LOSS。
第三步：
和之前的是一样的，现在的所有未知参数统称为，里面有很多的元素。现在就是找一组，使的LOSS最小。
步骤：
1.先选定一组随机初始的数值
.
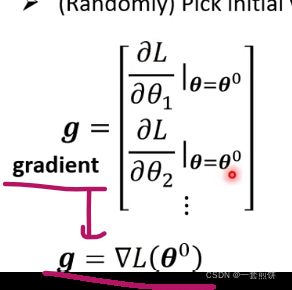
2.对中的么一个参数都进行微分的计算，集合起来就是一个向量，这个向量用g来表示。
（下面的是上面的简写的方法）
3.更新参数，更新的方法和两个参数的方法是一样的
4，一直更新到g向量是零向量。（实际上是不会更新到零向量的）
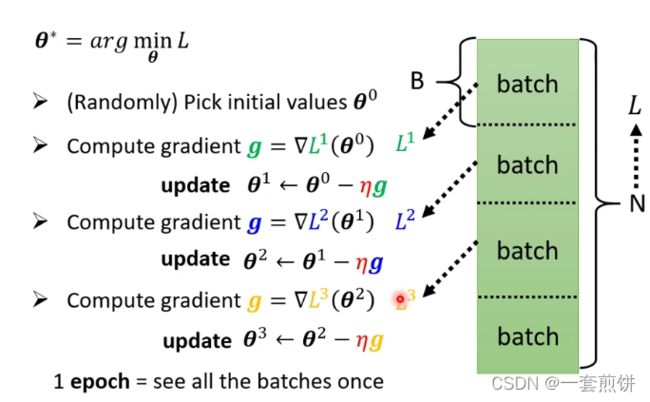
在实际应用是会遇到的问题：在做g的时候是将许多（N）的资料，随机分，分成的每一份资料叫做Bacth.每一个的Batch里面有B笔资料，现在我们只拿一个Batch里面的资料来算LOSS，用
来表示。用这个来计算g,,在继续更新参数，对每一个Batch都重复上面的步骤。这样把每一个Batch都计算一边的方法叫做1 epoch.每次更新一次参数叫做Update.
为什么要分一个个的Batch（等下周讲）
1 epoch和update的区别：
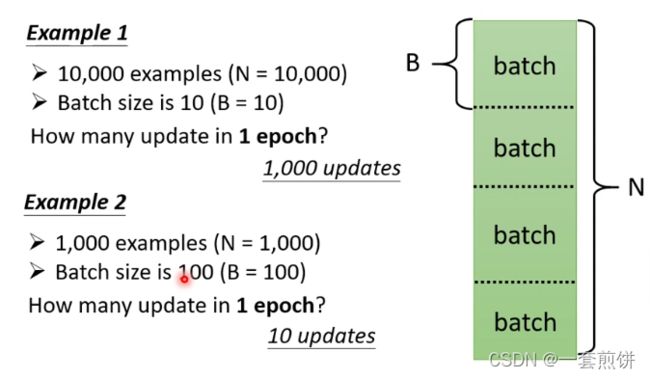
举例说明，假设N=10000，B=10（自己决定的，叫做Hyper Parameter），问在一个epoch当中一共update几次参数？
答案就是10000/10=1000个Batch.（1000个update）
第二个例子：假设N=1000,B=100（自己决定的,叫做Hyper Parameter）,问在一个epoch当中一共update几次参数？
答案就是1000/100=10个Batch.（10个update）
更新参数的大小是取决于Batch size的大小。
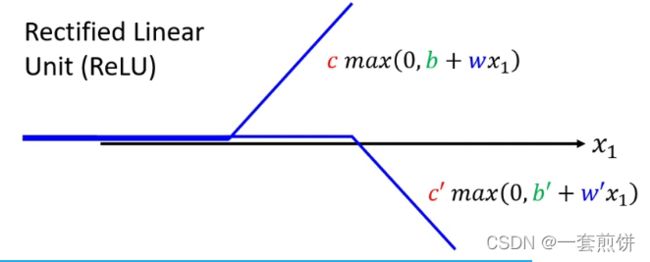
Hard Sigmoid 可以看作是由两个Rectified Linear Unit (ReLU)组成。
（括号当中是比较大小的，两者谁大，就输出的是大的），两个ReLU叠加起来就形成了Hard Sigmoid.如图所示：
如果不想用Sigmoid，而是用ReLU：
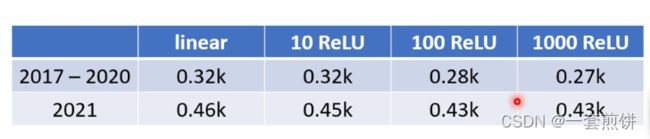
上面的这两种，哪一种比较好呢？（ReLU比较好）
在实际的实验当中：100个ReLU在2021年的预测数据相比较Linear的明显好很多，但是在1000 个ReLU的时候变化就不是很明显了。
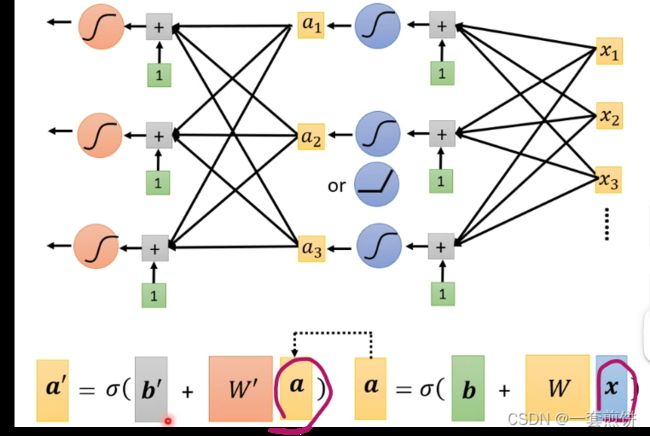
下面我们可以将Sigmoid这个过程多做几遍：
第一次产生的a当作是第二次的向量（相当于x）带入到第二次的Sigmoid当中。（这个或称的次数也是自己决定的）
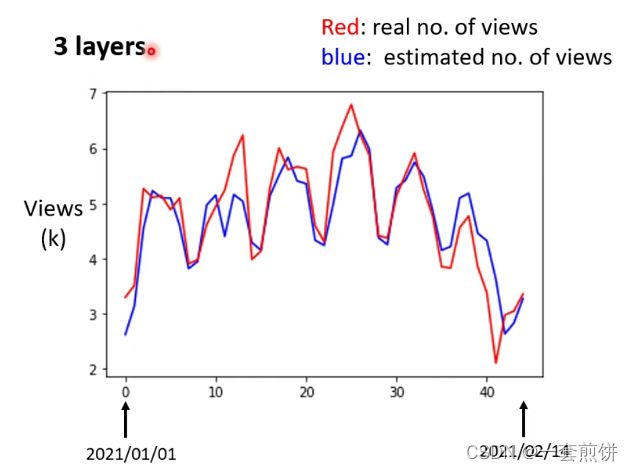
真实的实验结果如下图：（上面的过程做了三次ReLU之后得到的）
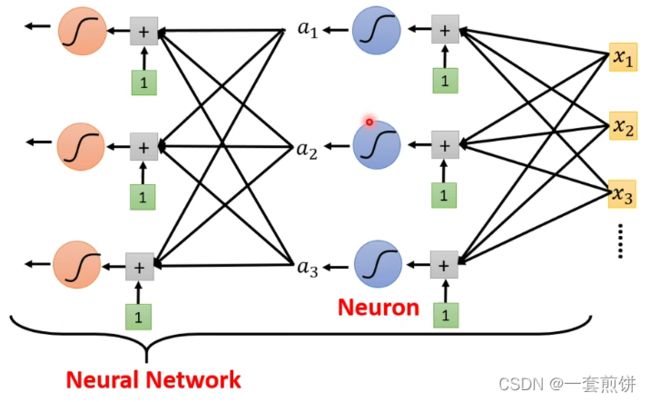
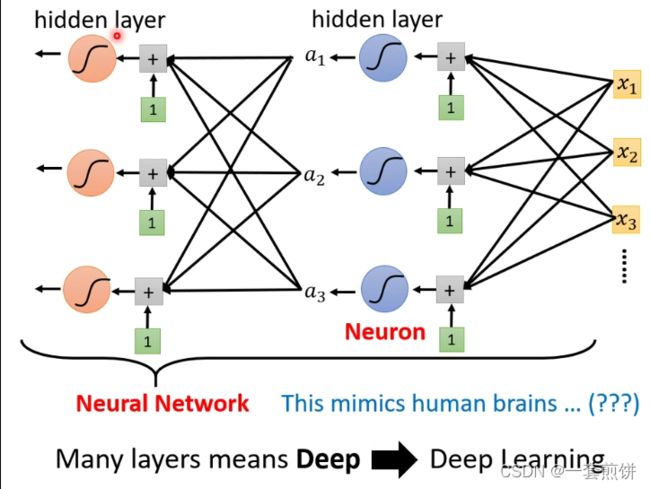
Neuron:(神经元)
（这个模型就是在模拟人脑）
Deep Learning
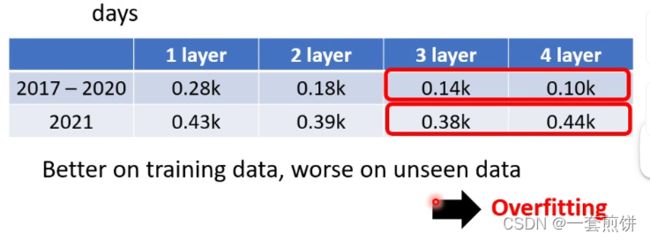
Overfitting：训练资料和预测资料结果不一样
我们现在做的就是预测某一天的资料使用3Layer还是4Layer?(如何选模型下周讲)
选3Layer的. 因为我们在意的结果是未来预测的资料,所以3Layer的预测资料是比4Layer好。
举例来说：统计的资料在2/24号，现在预测一下2/25号的观看的人数是多少。
现在3Layer说2/25号的观看人数是5.25k(先假设2/25的预测是对的，但是实际上我们不知道2/25的观看人数)，再用模型预测2/26号的观看人数，得到的结果是3.96k。（下周讲）